| 9. Ecuaciones diferenciales |
9.9. Ecuaciones lineales de orden superior
EN ESTE CAPÍTULO ampliamos los resultados obtenidos en el Capítulo 9.5 para ecuaciones lineales de segundo orden a ecuaciones lineales de orden superior.
LA SECCIÓN 9.9.1 presenta una introducción teórica a las ecuaciones lineales de orden superior.
LA SECCIÓN 9.9.2 analiza las ecuaciones homogéneas de coeficientes constantes de orden superior.
LA SECCIÓN 9.9.3 presenta el método de coeficientes indeterminados para ecuaciones de orden superior.
LA SECCIÓN 9.9.4 extiende el método de variación de parámetros a ecuaciones de orden superior.
9.9.1 INTRODUCCIÓN A LAS ECUACIONES LINEALES DE ORDEN SUPERIOR
Se dice que una ecuación diferencial de orden n es lineal si se puede escribir en la forma
y(n) + p1(x)y(n − 1) + · · · + pn(x)y = f (x). (9.9.1.1)
Consideramos ecuaciones de esta forma con n = 1 en la Sección 9.2.1 y con n = 2 en el Capítulo 9.5. En este capítulo, n es un entero positivo arbitrario.
En esta sección esbozamos la teoría general de las ecuaciones lineales de n-ésimo orden. Como esta teoría ya se ha discutido para n = 2 en las Secciones 9.5.1 y 9.5.3, omitiremos las demostraciones.
Por conveniencia, consideramos ecuaciones diferenciales lineales escritas como
P0(x)y(n) + P1(x)y(n − 1) + · · · + Pn(x)y = F(x), (9.9.1.2)
que se puede reescribir como (9.9.1.1) en cualquier intervalo en el que P0 no tenga ceros, con p1 = P1/P0, . . . , pn = Pn/P0 y f = F/P0. Para simplificar, a lo largo de este capítulo abreviaremos el lado izquierdo de (9.9.1.2) por Ly; esto es,
Ly = P0y(n) + P1y(n − 1) + · · · + Pny.
Decimos que la ecuación Ly = F es normal en (a, b) si P0, P1, . . . , Pn y F son continuas en (a, b) y P0 no tiene ceros en (a, b). Si esto es así, Ly = F se puede escribir como (9.9.1.1) con p1, . . . , pn y f continuas en (a, b).
El siguiente teorema es análogo al Teorema 9.5.3.1.
Teorema 9.9.1.1
Supongamos que Ly = F es normal en (a, b), sea x0 un punto en (a, b), y sea k0, k1, . . . , kn − 1 números reales arbitrarios. Entonces el problema de valor inicial
Ly = F, y(x0) = k0, y′(x0) = k1, . . ., y(n −1)(x0) = kn − 1
tiene solución única en (a, b). ♦
Ecuaciones Homogéneas
La ecuación (9.9.1.2) se dice que es homogénea si F ≡ 0 y no homogénea en caso contrario. Como y ≡ 0 es obviamente una solución de Ly = 0, la llamamos solución trivial. Cualquier otra solución es no trivial.
Si y1, y2, . . . , yn se definen en (a, b) y c1, c2, . . . , cn son constantes, entonces
y = c1y1 + c2y2 + · · · + cnyn (9.9.1.3)
es una combinación lineal de {y1, y2 . . . , yn}. Es fácil demostrar que si y1, y2 . . . , yn son soluciones de Ly = 0 en (a, b), entonces también lo es cualquier combinación lineal de {y1, y2 . . . , yn}. (Véase la demostración del Teorema 9.5.1.2.) Decimos que {y1, y2 . . . , yn} es un conjunto fundamental de soluciones de Ly = 0 en (a, b) si cada solución de Ly = 0 en (a, b) se puede escribir como una combinación lineal de {y1, y2 . . . , yn}, como en (9.9.1.3). En este caso decimos que (9.9.1.3) es la solución general de Ly = 0 en (a, b).
Puede demostrarse (Ejercicios 14 y 15) que si la ecuación Ly = 0 es normal en (a, b), entonces tiene infinitos conjuntos fundamentales de soluciones en (a, b). La siguiente definición ayudará a identificar conjuntos fundamentales de soluciones de Ly = 0:
Decimos que {y1, y2 . . . , yn} es linealmente independiente de (a, b) si las únicas constantes c1, c2, . . . , cn tal que
c1y1(x) + c2y2(x) + · · · + cnyn(x) = 0, a < x < b, (9.9.1.4)
son c1 = c2 = · · · = cn = 0. Si (9.9.1.4) se cumple para algún conjunto de constantes c1, c2, . . . , cn que no son todos cero, entonces {y1, y2, . . ., yn} depende linealmente de (a, b).
El siguiente teorema es análogo al Teorema 9.5.1.3.
Teorema 9.9.1.2
Si Ly = 0 es normal en (a, b), entonces un conjunto {y1, y2 . . . , yn} de n soluciones de Ly = 0 en (a, b) es un conjunto fundamental si y solo si es linealmente independiente en (a, b). ♦
Ejemplo ilustrativo 9.9.1.1
La ecuación
x3y′′′ − x2y′′ − 2xy′ + 6y = 0 (9.9.1.5)
es normal y tiene las soluciones y1 = x2, y2 = x3 y y3 = 1/x en (−∞, 0) y (0, ∞). Demuestre que {y1, y2, y3 } es linealmente independiente en (−∞, 0) y (0, ∞). Luego encuentre la solución general de (9.9.1.5) en (−∞, 0) y (0, ∞).
Solución:
Suponer
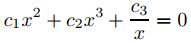
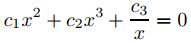
en (0, ∞). Debemos demostrar que c1 = c2 = c3 = 0. Derivando (9.9.1.6) dos veces se obtiene el sistema
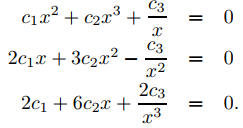
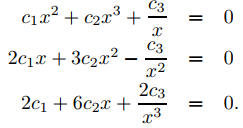
Si (9.9.1.7) se cumple para todo x en (0, ∞), entonces ciertamente se cumple en x = 1; por lo tanto,


Al resolver este sistema directamente, puedes verificar que solo tiene la solución trivial c1 = c2 = c3 = 0; sin embargo, para nuestros propósitos es más útil recordar del álgebra lineal que un sistema lineal homogéneo de n ecuaciones en n incógnitas solo tiene la solución trivial si su determinante es distinto de cero. Como el determinante de (9.9.1.8) es


se sigue que (9.9.1.8) tiene solo la solución trivial, por lo que {y1, y2, y3} es linealmente independiente en (0, ∞). Ahora el Teorema 9.9.1.2 implica que


es la solución general de (9.9.1.5) en (0, ∞). Para ver que esto también es cierto en (−∞, 0), suponga que (9.9.1.6) se cumple en (−∞, 0). Al establecer x = −1 en (9.9.1.7) se obtiene
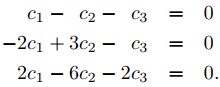
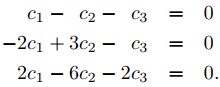
Como el determinante de este sistema es
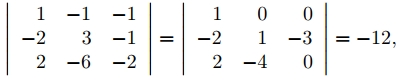
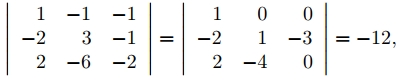
se sigue que c1 = c2 = c3 = 0; es decir, {y1, y2, y3} es linealmente independiente en (−∞, 0). ♦
Ejemplo ilustrativo 9.9.1.2
La ecuación
y(4) + y′′′ − 7y′′ − y′ + 6y = 0 (9.9.1.9)
es normal y tiene las soluciones y1 = ex, y2 = e−x, y3 = e2x y y4 = e−3x en (−∞, ∞). (Verifique). Demuestre que {y1, y2, y3, y4} es linealmente independiente en (−∞, ∞). Luego encuentre la solución general de (9.9.1.9).
Solución:
Suponga que c1, c2, c3 y c4 son constantes tales que
c1ex + c2e−x + c3e2x + c4e−3x = 0 (9.9.1.10)
para todo x. Debemos demostrar que c1 = c2 = c3 = c4 = 0. Derivando (9.9.1.10) tres veces se obtiene el sistema
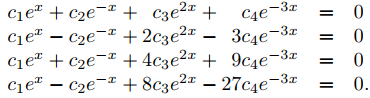
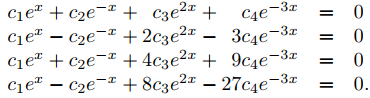
Si (9.9.1.11) se cumple para todo x, entonces ciertamente se cumple para x = 0. Por lo tanto
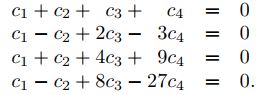
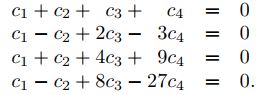
El determinante de este sistema es


entonces el sistema tiene solo la solución trivial y1 = y2 = y3 = y4 = 0. Ahora el teorema 9.9.1.2 implica que
y = c1ex + c2e−x + c3e2x + c4e−3x
es la solución general de (9.9.1.9). ♦
El wronskiano
Podemos aplicar el método usado en los ejemplos 9.9.1.1 y 9.9.1.2 para probar n soluciones {y1, y2, . . ., yn} de cualquier ecuación de n-ésimo orden Ly = 0 para independencia lineal en un intervalo (a, b) en el que la ecuación es normal.
Así, si c1, c2 ,. . . , cn son constantes tales que
c1y1 + c2y2 + · · · + cnyn = 0, a < x < b,
luego de derivar n − 1 veces se obtiene el siguiente sistema de ecuaciones n × n


para c1, c2, . . . , cn. Para una x fija, el determinante de este sistema es


Llamamos a este determinante el Wronskiano de {y1, y2, . . ., yn}. Si W(x) ≠ 0 para alguna x en (a, b), entonces el sistema (9.9.1.13) tiene solo la solución trivial c1 = c2 = · · · = cn = 0, y el Teorema 9.9.1.2 implica que
y = c1y1 + c2y2 + · · · + cnyn
es la solución general de Ly = 0 en (a, b).
El siguiente teorema generaliza el Teorema 9.5.1.4. La prueba se esboza en (Ejercicios 17 a 20).
Teorema 9.9.1.3
Supongamos que la ecuación lineal homogénea de n-ésimo orden
P0(x)y(n) + P1(x)yn − 1 + · · · + Pn(x)y = 0 (9.1.14)
es normal en (a, b), sean y1, y2, . . . , yn soluciones de (9.9.1.14) en (a, b), y sea x0 en (a, b). Entonces el wronskiano de {y1, y2, . . . , yn} está dado por


Por lo tanto, W no tiene ceros en (a, b) o W ≡ 0 en (a, b). ♦
La fórmula (9.1.15) es la fórmula de Abel.
El siguiente teorema es análogo al Teorema 9.5.1.6.
Teorema 9.9.1.4
Suponga que Ly = 0 es normal en (a, b) y sean y1, y2, . . . , yn n soluciones de Ly = 0 en (a, b). Entonces las siguientes declaraciones son equivalentes; es decir, son todas verdaderas o todas falsas:
(a) La solución general de Ly = 0 en (a, b) es y = c1y1 + c2y2 + · · · + cnyn.
(b) {y1, y2, . . . , yn} es un conjunto fundamental de soluciones de Ly = 0 en (a, b).
(c) {y1, y2, . . . , yn} es linealmente independiente de (a, b).
(d) El wronskiano de {y1, y2, . . . , yn} es distinto de cero en algún punto en (a, b).
(e) El wronskiano de {y1, y2, . . . , yn} es distinto de cero en todos los puntos en (a, b). ♦
Ejemplo ilustrativo 9.9.1.3
En el ejemplo 9.9.1.1 vimos que las soluciones y1 = x2, y2 = x3 e y3 = 1/x de
x3y′′′ − x2y′′ − 2xy′ + 6y = 0
son linealmente independientes en (−∞, 0) y (0, ∞). Calcula el Wronskiano de {y1, y2, y3}.
Solución:
Si x ≠ 0, entonces


donde factorizamos x2, x y 2 de la primera, segunda y tercera fila de W(x), respectivamente. Sumando la segunda fila del último determinante a la primera y tercera filas se obtiene


Por lo tanto W(x) ≠ 0 en (−∞, 0) y (0, ∞). ♦
Ejemplo ilustrativo 9.9.1.4
En el ejemplo 9.9.1.2 vimos que las soluciones y1 = ex, y2 = e−x, y3 = e2x y y4 = e−3x de
y(4) + y′′′ − 7y′′ − y′ + 6y = 0
son linealmente independientes en todo intervalo abierto. Calcula el Wronskiano de {y1, y2, y3, y4}.
Solución:
Para todo x,
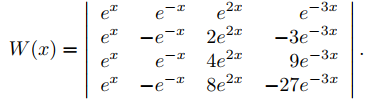
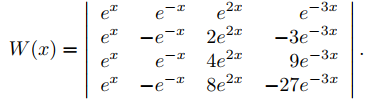
Al sacar el factor común exponencial de cada fila se obtiene


de (9.9.1.12). ♦
OBSERVACIÓN: Bajo los supuestos del Teorema 9.9.1.4, no es necesario obtener una fórmula para W(x). Simplemente evalúe W(x) en un punto conveniente en (a, b), como hicimos en los ejemplos 9.9.1.1 y 9.9.1.2.
Teorema 9.9.1.5
Supongamos que c está en (a, b) y α1, α2, . . ., son números reales, no todos cero. Bajo los supuestos del Teorema 9.10.3.3, suponga que y1 e y2 son soluciones de (9.5.1.35) tales que
αyi(c) + yi′(c) + · · · + yi(n − 1)(c) = 0, 1 ≤ i ≤ n. (9.9.1.16)
Entonces {y1, y2, . . . yn} no es linealmente independiente en (a, b). ♦
Prueba;
Dado que α1, α2, . . . , αn no son todos cero, (9.9.1.14) implica que


de esta manera


y el Teorema 9.9.1.4 implica la conclusión establecida. ♦
Solución general de una ecuación no homogénea
El siguiente teorema es análogo al Teorema 9.5.3.2. Muestra cómo encontrar la solución general de Ly = F si conocemos una solución particular de Ly = F y un conjunto fundamental de soluciones de la ecuación complementaria Ly = 0.
Teorema 9.9.1.6
Supongamos que Ly = F es normal en (a, b). Sea yp una solución particular de Ly = F en (a, b), y sea {y1, y2, . . ., yn} un conjunto fundamental de soluciones de la ecuación complementaria Ly = 0 en (a, b). Entonces y es una solución de Ly = F en (a, b) si y solo si
y = yp + c1y1 + c2y2 + · · · + cnyn,
donde c1, c2, . . ., cn son constantes. ♦
El siguiente teorema es análogo al Teorema 9.5.3.2.
Teorema 9.9.1.7 [El principio de superposición]
Supongamos que para cada i = 1, 2, . . . , r, la función ypi es una solución particular de Ly = Fi en (a, b). Entonces
yp = yp1 + yp2 + · · · + ypr
en (a, b). ♦
Aplicaremos los teoremas 9.9.1.6 y 9.9.1.7 en el resto de este capítulo.
