| 1. Funciones y sus gráficas |
1.5. Funciones exponenciales y logarítmicas: Objetivos de aprendizaje
1.5.1. Identifica la forma de una función exponencial.
1.5.2. Explica la diferencia entre las gráficas de xᵇ y bˣ.
1.5.3. Reconocer la importancia del número e.
1.5.4. Identifica la forma de una función logarítmica.
1.5.5. Explicar la relación entre funciones exponenciales y logarítmicas.
1.5.6. Describe cómo calcular un logaritmo en una base diferente.
1.5.7. Identifique las funciones hiperbólicas, sus gráficos e identidades básicas.
En esta sección examinamos las funciones exponenciales y logarítmicas. Utilizamos las propiedades de estas funciones para resolver ecuaciones que implican términos exponenciales o logarítmicos, y estudiamos el significado y la importancia del número e. También definimos funciones hiperbólicas e hiperbólicas inversas, que implican combinaciones de funciones exponenciales y logarítmicas. (Tenga en cuenta que presentamos definiciones alternativas de funciones exponenciales y logarítmicas en el capítulo Aplicaciones de la integral, y demostramos que las funciones tienen las mismas propiedades con cualquier definición).
Funciones exponenciales
Las funciones exponenciales surgen en muchas aplicaciones. Un ejemplo común es el crecimiento de una población.
Por ejemplo, si una población comienza con P₀ individuos y luego crece a una tasa anual del 2%, su población después de 1 año es
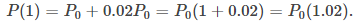
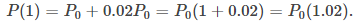
Su población después de 2 años es
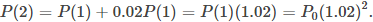
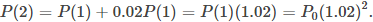
En general, su población después de t años es
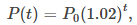
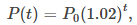
que es una función exponencial Más generalmente, cualquier función de la forma f (x) = bˣ, donde b > 0, b ≠ 1, es una función exponencial con base b y exponente x. Las funciones exponenciales tienen bases constantes y exponentes variables. Tenga en cuenta que una función de la forma f (x) = xᵇ para alguna constante b no es una función exponencial sino una función de potencia.
Para ver la diferencia entre una función exponencial y una función de potencia, comparamos las funciones y = x² e y = 2ˣ. En la Tabla 1.5_1, vemos que tanto 2ˣ como x² se aproximan al infinito cuando x → ∞. Eventualmente, sin embargo, 2ˣ se vuelve más grande que x² y crece más rápidamente cuando x → ∞. En la dirección opuesta, cuando x → −∞, x² → ∞, mientras que 2ˣ → 0. La recta y = 0 es una asíntota horizontal para y = 2ˣ.
| x | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| x² | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 | 25 | 36 |
| 2ˣ | 1/8 | 1/4 | 1/2 | 1 | 2 | 4 | 8 | 16 | 32 | 64 |
(Tabla1.5_1 Valores de x² y 2ˣ)
En la Figura 1.5_1, graficamos y =x² e y = 2ˣ para mostrar cómo difieren las gráficas.
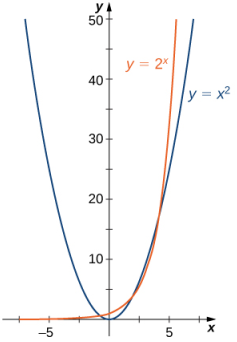

(Figura 1.5_1 Tanto 2ˣ como x² se aproximan al infinito cuando x → ∞, pero 2ˣ crece más rápidamente que x². Cuando x → −∞, x² → ∞, mientras que 2ˣ → 0.)
Evaluación de funciones exponenciales
Recordemos las propiedades de los exponentes: si x es un entero positivo, entonces definimos bˣ = b⋅b ⋯ b (con x factores de b). Si x es un entero negativo, entonces x = −y para algún entero positivo y, y definimos bˣ = b⁻ʸ = 1/bʸ. Además, bº se define como 1. Si x es un número racional, entonces x = p/q, donde p y q son enteros y

Por ejemplo,





| x | 1.4 | 1.41 | 1.414 | 1.4142 | 1.41421 | 1.414213 |
| 2ˣ | 2.639 | 2.65737 | 2.66475 | 2.665119 | 2.665138 | 2.665143 |
(Tabla 1.5_2 Valores de 2ˣ para una lista de números racionales que se aproximan a 2^√2)
Ejemplo ilustrativo 1.5_1 Crecimiento bacterial
Suponga que se sabe que una población particular de bacterias duplica su tamaño cada 4 horas. Si un cultivo comienza con 1000 bacterias, el número de bacterias después de 4 horas es n(4) = 1000⋅2. El número de bacterias después de 8 horas es n(8) = n(4) ⋅2 = 1000⋅2². En general, el número de bacterias después de 4m horas es n(4m) = 1000⋅2 ͫ . Dejando t = 4 ͫ , vemos que el número de bacterias después de t horas es

Solución:
El número de bacterias después de 6 horas viene dado por

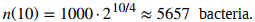
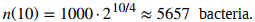
EJERCICIO DE CONTROL 1.5_1
Dada la función exponencial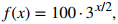
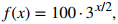
Graficar funciones exponenciales
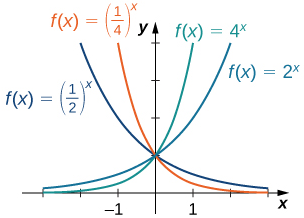
Para cualquier base b > 0, b ≠ 1, la función exponencial f (x) = bˣ se define para todos los números reales x y bˣ > 0. Por lo tanto, el dominio de f (x) = bˣ es (−∞, ∞) y el rango es (0, ∞). Para graficar bˣ, notamos que para b > 1, bˣ aumenta en (−∞, ∞) y bˣ → ∞ cuando x → ∞, mientras que bˣ → 0 cuando x → −∞. Por otro lado, si 0 < b < 1, f (x) = bˣ está disminuyendo en (−∞, ∞) y bˣ → 0 cuando x → ∞ mientras que bˣ → ∞ cuando x → −∞ (Figura 1.5_2).

Tenga en cuenta que las funciones exponenciales satisfacen las leyes generales de los exponentes. Para recordarle estas leyes, las declaramos como reglas.
REGLA 1.5_1: LEYES DE LOS EXPONENTES
|
Para las constantes a > 0, b > 0 y para todas las x e y,
|
Ejemplo ilustrativo 1.5_2 Usando las leyes de los exponentes
Usa las leyes de los exponentes para simplificar cada una de las siguientes expresiones.
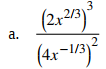
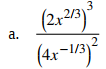


Solución:
a. Podemos simplificar de la siguiente manera:
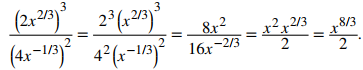
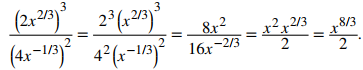
b. Podemos simplificar de la siguiente manera:
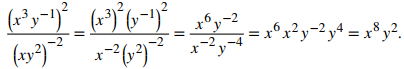
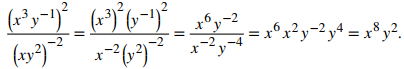
EJERCICIO DE CONTROL 1.5_2
Usa las leyes de los exponentes para simplificar (6x⁻³3y²)/(12x⁻⁴y⁵).

