| 9. Ecuaciones diferenciales | 9.9. Ecuaciones lineales de orden superior |
9.9.4 Variación de parámetros para ecuaciones de orden superior
Derivación del método
Asumimos a lo largo de esta sección que la ecuación lineal no homogénea
P0(x)y(n) + P1(x)y(n − 1) + · · · + Pn(x)y = F(x) (9.9.4.1)
es normal en un intervalo (a, b). Abreviaremos esta ecuación como Ly = F, donde
Ly = P0(x)y(n) + P1(x)y(n − 1) + · · · + Pn(x)y.
Cuando hablamos de soluciones de esta ecuación y su ecuación complementaria Ly = 0, nos referimos a soluciones de (a, b). Mostraremos cómo utilizar el método de variación de parámetros para encontrar una solución particular de Ly = F, siempre que conozcamos un conjunto fundamental de soluciones {y1, y2, . . ., yn} de Ly = 0.
Buscamos una solución particular de Ly = F en la forma
yp = u1y1 + u2y2 + · · · + unyn (9.9.4.2)
donde {y1, y2, . . ., yn} es un conjunto fundamental conocido de soluciones de la ecuación complementaria
P0(x)y(n) + P1(x)y(n − 1) + · · · + Pn(x)y = 0
y u1, u2, . . . , un son funciones por determinar. Comenzamos imponiendo las siguientes n − 1 condiciones a u1, u2, . . . , un:


Estas condiciones conducen a fórmulas simples para las primeras n − 1 derivadas de yp:
yp(r) = u1y1(r) + u2y2(r) · · · + unyn(r), 0 ≤ r ≤ n − 1. (9.9.4.4)
Estas fórmulas son fáciles de recordar, ya que parece que las obtuvimos derivando (9.9.4.2) n − 1 veces mientras tratamos u1, u2, . . . , un como constantes. Para ver que (9.9.4.3) implica (9.9.4.4), primero derivamos (9.9.4.2) para obtener
yp′ = u1y1′ + u2y2′ + · · · + unyn′ + u1′y1 + u2′y2 + · · · + un′yn,
lo que se reduce a
yp′ = u1y1′ + u2y2′ + · · · + unyn′
debido a la primera ecuación en (9.9.4.3). Diferenciando la ecuación anterior, se obtiene


lo que se reduce a


debido a la segunda ecuación en (9.9.4.3). Continuando de esta manera se llega a (9.9.4.4).
La última ecuación en (9.9.4.4) es
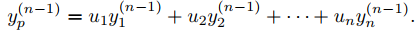
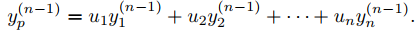
Diferenciando, se obtiene


Sustituyendo la ecuación anterior y (9.9.4.4) en (9.9.4.1), se obtiene


Dado que Lyi = 0 (1 ≤ i ≤ n), esto se reduce a
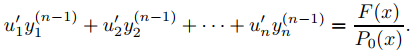
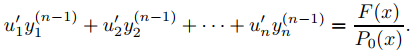
Combinando esta ecuación con (9.9.4.3) se muestra que
yp = u1y1 + u2y2 + · · · + unyn
es una solución de (9.9.4.1) si
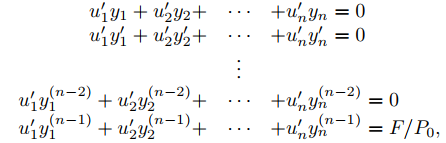
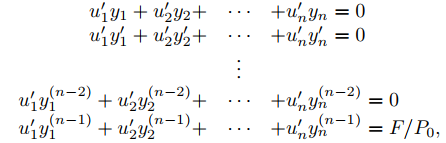
que se puede escribir en forma matricial como


El determinante de este sistema es el Wronskiana W del conjunto fundamental de soluciones {y1, y2, . . ., yn}, que no tiene ceros en (a, b), según el Teorema 9.9.1.4. Resolviendo (9.9.4.5) según la regla de Cramer, se obtiene


donde Wj es el Wronskiano del conjunto de funciones obtenidas eliminando yj de {y1, y2, . . ., yn} y manteniendo el resto de funciones en el mismo orden. De manera equivalente, Wj es el determinante obtenido al eliminar la última fila y la j-ésima columna de W.
Habiendo obtenido u1′, u2′, . . ., un′, podemos integrar para obtener u1, u2, . . ., un. Como en la Sección 9.5.7, tomamos las constantes de integración como cero y eliminamos cualquier combinación lineal de {y1, y2, . . ., yn} que puede aparecer en yp.
COMENTARIO: Para lograr eficiencia, es mejor calcular W1, W2, . . . , Wn primero y luego calcular W expandiendo los cofactores de la última fila; de este modo,


Ecuaciones de tercer orden
Si n = 3, entonces


Por lo tanto


y (9.9.4.6) se convierte en
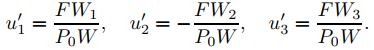
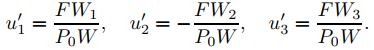
Ejemplo ilustrativo 9.9.4.1
Encuentre una solución particular de
xy′′′ − y′′ − xy′ + y = 8x2ex, (9.9.4.8)
dado que y1 = x, y2 = ex e y3 = e−x forman un conjunto fundamental de soluciones de la ecuación complementaria. Luego encuentre la solución general de (9.9.4.8).
Solución:
Buscamos una solución particular de (9.9.4.8) de la forma
yp = u1x + u2ex + u3e−x.
El wronskiano de {y1, y2, y3} es


por lo que
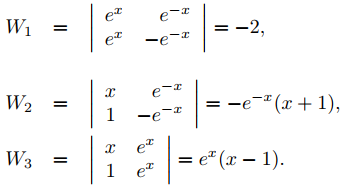
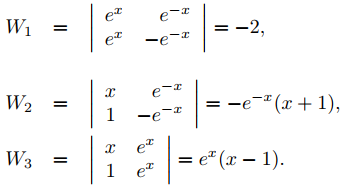
Al expandir W por los cofactores de la última fila, se obtiene


Dado que F(x) = 8x2ex y P0(x) = x,


Por lo tanto, de (9.9.4.7)
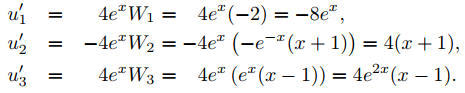
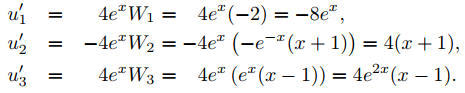
Al integrar y tomar las constantes de integración como cero, se obtiene
u1 = −8ex, u2 = 2(x + 1)2, u3 = e2x(2x − 3).
Por eso,
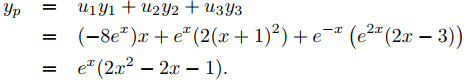
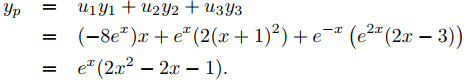
Como −ex es una solución de la ecuación complementaria, redefinimos
yp = 2xex(x − 1).
Por tanto la solución general de (9.9.4.8) es
y = 2xex(x − 1) + c1x + c2ex + c3e−x. ♦
Ecuaciones de cuarto orden
Si n = 4, entonces
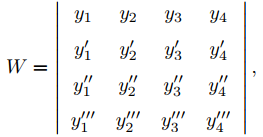
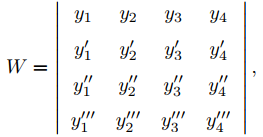
Por lo tanto
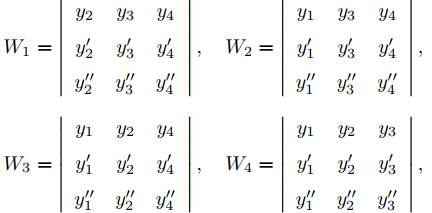
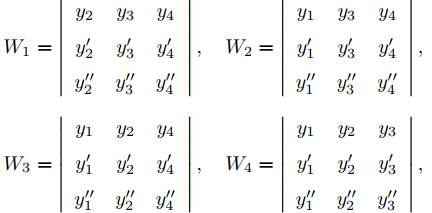
y (9.9.4.6) se convierte en


Ejemplo ilustrativo 9.9.4.2
Encuentre una solución particular de
x4y(4) + 6x3y′′′ + 2x2y′′ − 4xy′ + 4y = 12x2, (9.9.4.10)
dado que y1 = x, y2 = x2, y3 = 1/x e y4 = 1/x2 forman un conjunto fundamental de soluciones de la ecuación complementaria. Luego encuentre la solución general de (9.9.4.10) sobre (−∞, 0) y (0, ∞).
Solución:
Buscamos una solución particular de (9.9.4.10) de la forma


El wronskiano de {y1, y2, y3, y4} es


por lo que


Al expandir W por los cofactores de la última fila, se obtiene


Dado que F(x) = 12x2 y P0(x) = x4,


Por lo tanto, de (9.9.4.9),


Al integrarlos y tomar las constantes de integración como cero, se obtiene
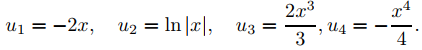
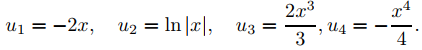
Por eso,
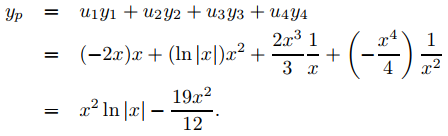
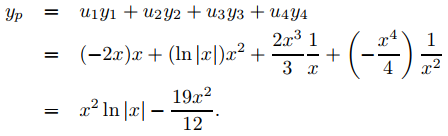
Como −19x2/12 es una solución de la ecuación complementaria, redefinimos
yp = x2 ln|x|.
Por lo tanto


es la solución general de (9.9.4.10) sobre (−∞, 0) y (0, ∞). ♦
