| 3. La derivada |

La derivada como función: Objetivos de aprendizaje

3.2.1. Definir la función derivada de una función.
3.2.2. Graficar una función derivada a partir de la gráfica de una función dada.
3.2.3. Indicar la conexión entre derivadas y continuidad.
3.2.4. Describir tres condiciones para cuando una función no tiene una derivada.
3.2.5. Explicar el significado de una derivada de orden superior.

Como hemos visto, la derivada de una función en un punto dado nos da la tasa de cambio o la pendiente de la recta tangente a la función en ese punto. Si diferenciamos una función de posición en un momento dado, obtenemos la velocidad en ese momento. Parece razonable concluir que conocer la derivada de la función en cada punto produciría información valiosa sobre el comportamiento de la función, razonamiento correcto. Sin embargo, el proceso de encontrar la derivada incluso en un puñado de valores utilizando las técnicas de la sección anterior rápidamente se volvería bastante tedioso. En esta sección definimos la función derivada y aprendemos un proceso para encontrarla.

La derivada de una función

La función derivada proporciona la derivada de una función en cada punto del dominio de la función original para la que se define la derivada. Podemos definir formalmente una función derivada de la siguiente manera.

DEFINICIÓN 3.2_1. La función derivada o la derivada de una función

Sea y = f (x) una función. La función derivada de f, denotada por f ′, es una función en x tal que el siguiente límite existe:

Se dice que una función f (x) es diferenciable en a si existe f ′(a). De manera más general, se dice que una función es diferenciable en un conjunto abierto S si es diferenciable en cada punto del conjunto S, y una función diferenciable es aquella en la que f ‘(x) existe en su dominio.

En los siguientes ejemplos ilustrativos usamos la ecuación proporcionada en la definición 3.2_1 para encontrar la derivada de una función.

Ejemplo ilustrativo 3.2_1. Encontrar la derivada de una función de raíz cuadrada

Encuentre la derivada de f (x) = √x.

Solución:

Comience directamente con la definición de la función derivada.

Sustituya f (x + h) = √(x + h)  y  f (x) = √x  en  f ′ (x) = lim_{h → 0} [f (x + h) – f (x)]/h:

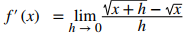
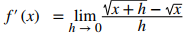
Multiplique el numerador y el denominador por √(x + h) + √x sin distribuir en el denominador:

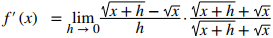
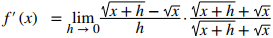
Multiplique los numeradores y simplifique:

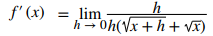
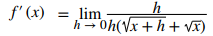
Cancele la h:

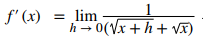
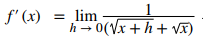
Por último, evalúe el límite:

◊

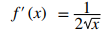
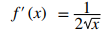
Ejemplo ilustrativo 3.2_2. Encontrar la derivada de una función cuadrática

Encuentre la derivada de la función f (x) = x² − 2x.

Solución:

Siga el mismo procedimiento aquí que en la solución del ejemplo anterior, pero sin tener que multiplicar por el conjugado.

Sustituya f (x + h) = (x + h)² – 2(x + h)  y  f (x) = x² – 2x  en  f ′ (x) = lim_{h → 0} [f (x + h) – f (x)]/h:

Expanda (x + h)² – 2(x + h):

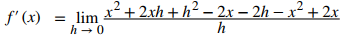
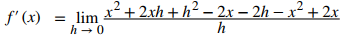
Reduzca términos semejantes:

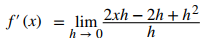
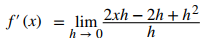
Factorice por h en el numerador:

Cancele el factor común h:

Por último, evalúe el límite:

◊

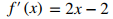
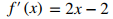
Se puede usars una variedad de notaciones diferentes para expresar la derivada de una función. En el ejemplo 3.2_2 mostramos que si f (x) = x² − 2x, entonces f ′(x) = 2x − 2. Si hubiéramos expresado esta función en la forma y = x² − 2x, podríamos haber expresado la derivada como y′ = 2x − 2 o dy/dx = 2x − 2. Podríamos haber transmitido la misma información escribiendo d/dx (x² − 2x) = 2x − 2. Por lo tanto, para la función y = f (x), cada una de las siguientes notaciones representa la derivada de f (x):

En lugar de f ′(a) también podemos usar

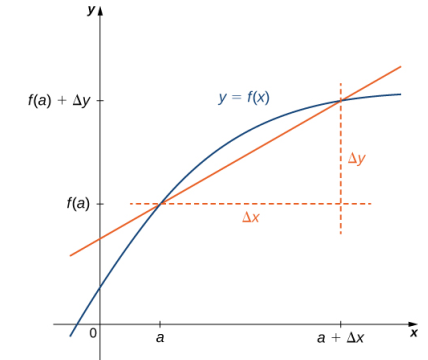
El uso de la notación dy/dx (llamada notación de Leibniz) es bastante común en ingeniería y física. Para comprender mejor esta notación, recuerde que la derivada de una función en un punto es el límite de las pendientes de las rectas secantes a medida que estas rectas secantes se acercan a la recta tangente. Las pendientes de las rectas secantes a menudo se expresan en la forma Δy/Δx donde Δy es la diferencia en los valores de y correspondientes a la diferencia en los valores de x, que se expresan como Δx (Figura 3.2_1). Así, la derivada, que puede considerarse como la tasa de cambio instantánea de y con respecto a x, se expresa como

Graficando una derivada

Ya hemos discutido cómo graficar una función, por lo tanto, dada la ecuación de una función o la ecuación de una función derivada, podríamos graficarla. Dado ambos, esperaríamos ver una correspondencia entre las gráficas de estas dos funciones, ya que f ′(x) da la tasa de cambio de una función f (x) (o pendiente de la recta tangente a f (x)).

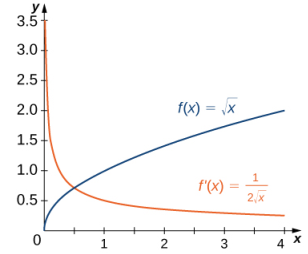
En el ejemplo 3.2_1 encontramos que para f (x) = √x,  f ′(x) = 1/√x. Si graficamos estas funciones en los mismos ejes, como en la Figura 3.1_2, podemos usar las gráficas para comprender la relación entre estas dos funciones. Primero, notamos que f (x) está aumentando en todo su dominio, lo que significa que las pendientes de sus rectas tangentes en todos los puntos son positivas. En consecuencia, esperamos f ′(x) > 0 para todos los valores de x en su dominio. Además, a medida que x aumenta, las pendientes de las rectas tangentes a f (x) disminuyen y esperamos ver una disminución correspondiente en f ′(x). También observamos que f (0) no está definida y que el lim_{x→ 0+} f ′(x) = + ∞, correspondiente a una tangente vertical a f (x) en 0.

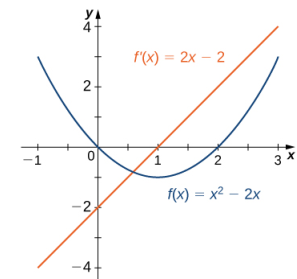
En el ejemplo 3.2_2 encontramos que para f (x) = x² − 2x,  f ′(x) = 2x − 2. Las gráficas de estas funciones se muestran en la figura 3.1_3. Observe que f (x) está decreciendo para x < 1. Para estos mismos valores de x, f  ′(x) < 0. Para valores de x > 1, f (x) aumenta y f ′ (x) > 0. Además, f (x) tiene una tangente horizontal en x = 1 y f ′(1) = 0.

Ejemplo ilustrativo 3.2_3. Trazar la gráfica de una derivada usando una función

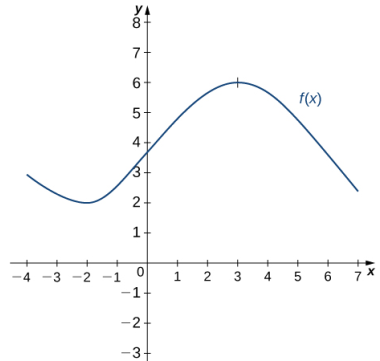
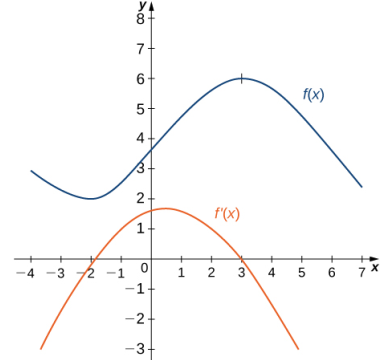
Use la siguiente gráfica de una función f (x) para dibujar la gráfica correspondiente de f ′(x).

Solución:
La solución se muestra en la siguiente gráfica. Observe que f (x) está creciendo y f ′(x) > 0 en (–2, 3). Además, f (x) está decreciendo y f ′(x) < 0 en (−∞, −2) y en (3, +∞). También tenga en cuenta que f (x) tiene tangentes horizontales en –2 y 3, y f ′(- 2) = 0 y f ′(3) = 0.

◊