| 9. Ecuaciones diferenciales | Ejercicios resueltos del capítulo 9 |
9.10. Sistemas lineales de ecuaciones diferenciales: Objetivos de aprendizaje
EN ESTE CAPÍTULO consideramos sistemas de ecuaciones diferenciales que involucran más de una función desconocida. Estos sistemas surgen en muchas aplicaciones físicas.
La SECCIÓN 9.10.1 presenta ejemplos de situaciones físicas que conducen a sistemas de ecuaciones diferenciales.
La SECCIÓN 9.10.2 analiza los sistemas lineales de ecuaciones diferenciales.
La SECCIÓN 9.10.3 trata de la teoría básica de sistemas lineales homogéneos.
LAS SECCIONES 9.10.4, 9.10.5 y 9.10.6 presentan la teoría de sistemas homogéneos con coeficientes constantes.
La SECCIÓN 9.10.7 presenta el método de variación de parámetros para sistemas lineales no homogéneos.
9.10.1 INTRODUCCIÓN A SISTEMAS DE ECUACIONES DIFERENCIALES
Muchas situaciones físicas se modelan mediante sistemas de n ecuaciones diferenciales en n funciones desconocidas, donde n ≥ 2. Los siguientes tres ejemplos ilustran problemas físicos que conducen a sistemas de ecuaciones diferenciales. En estos ejemplos y a lo largo de este capítulo, denotaremos la variable independiente por t.
Ejemplo ilustrativo 9.10.1_1
Los tanques T1 y T2 contienen 100 galones y 300 galones de soluciones salinas, respectivamente. Las soluciones de sal se agregan simultáneamente a ambos tanques desde fuentes externas, se bombean de un tanque al otro y se drenan de ambos tanques (Figura 9.10.1_1). Una solución con 1 libra de sal por galón se bombea a T1 desde una fuente externa a 5 gal/min, y una solución con 2 libras de sal por galón se bombea a T2 desde una fuente externa a 4 gal/min. La solución de T1 se bombea a T2 a 2 gal/min y la solución de T2 se bombea a T1 a 3 gal/min. T1 se drena a 6 gal/min y T2 se drena a 3 gal/min. Sean Q1(t) y Q2(t) el número de libras de sal en T1 y T2, respectivamente, en el tiempo t > 0. Deduzca un sistema de ecuaciones diferenciales para Q1 y Q2. Suponga que ambas mezclas están bien agitadas.
Solución:
Como en la sección 9.4.2, deje que la tasa de entrada y la tasa de salida denoten las tasas (lb/min) a las que la sal entra y sale de un tanque; por lo tanto,
Q′1 = (tasa de entrada)1 − (tasa de salida)1,
Q′2 = (tasa de entrada)2 − (tasa de salida)2.
Tenga en cuenta que los volúmenes de las soluciones en T1 y T2 permanecen constantes en 100 galones y 300 galones, respectivamente.
◊ T1 recibe sal de la fuente externa a razón de
(1 lb/gal) × (5 gal/min) = 5 lb/min,
y de T2 a razón de
Por lo tanto
(tasa de entrada)1 = 5 + (1/100)Q2. (9.10.1.1)
La solución sale de T1 a una velocidad de 8 gal/min, ya que se drenan 6 gal/min y se bombean 2 gal/min a T2; por eso,
(tasa de salida)1 = (lb/gal entrada T1)×(8 gal/min) = (1/100)Q1×8 = (2/25)Q1. (9.10.1.2)
Las ecuaciones (9.10.1.1) y (9.10.1.2) implican que
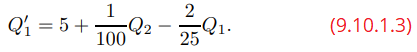
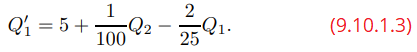
T2 recibe sal de la fuente externa a una tasa de
(2 lb/gal) × (4 gal/min) = 8 lb/min,
y de T1 a razón de
Por lo tanto
(tasa entrada)2 = 8 + (1/50)Q1. (9.10.1.4)
La solución sale de T2 a una velocidad de 6 gal/min, ya que se drenan 3 gal/min y se bombean 3 gal/min a T1; por eso,
(tasa de salida)2 = (lb/gal en T2)×(6 gal/min) = (1/300)Q2 × 6 = 150Q2. (9.10.1.5)
Las ecuaciones (9.10.1.4) y (9.10.1.5) implican que
Decimos que (9.10.1.3) y (9.10.1.6) forman un sistema de dos ecuaciones de primer orden en dos incógnitas, y las escribimos juntas como
Ejemplo ilustrativo 9.10.1_2
Una masa m1 está suspendida de un soporte rígido en un resorte S1 y una segunda masa m2 está suspendida de la primera en un resorte S2 (Figura 9.10.1_2). Los resortes obedecen a la ley de Hooke, con constantes de resorte k1 y k2. La fricción interna hace que los resortes ejerzan fuerzas de amortiguación proporcionales a las tasas de cambio de sus longitudes, con constantes de amortiguación c1 y c2. Sean y1 = y1(t) y y2 = y2(t) los desplazamientos de las dos masas desde sus posiciones de equilibrio en el tiempo t, medidos positivos hacia arriba.
Deduzca un sistema de ecuaciones diferenciales para y1 e y2, asumiendo que las masas de los resortes son despreciables y que las fuerzas verticales externas F1 y F2 también actúan sobre los objetos.
Solución:
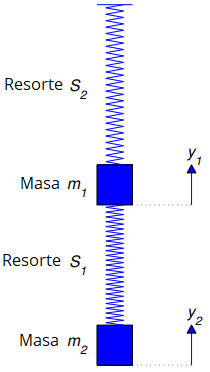
(Figura 9.10.1_2)
En equilibrio, S1 admite tanto m1 como m2 y S2 solo admite m2. Por lo tanto, si ∆l1 y ∆l2 son los alargamientos de los resortes en equilibrio, entonces
(m1 + m2)g = k1∆l1 y m2g = k2l2. (9.10.1.7)
Sea H1 la fuerza de la ley de Hooke que actúa sobre m1 y sea D1 la fuerza de amortiguación sobre m1. De manera similar, sean H2 y D2 la ley de Hooke y las fuerzas de amortiguación que actúan sobre m2. Según la segunda ley del movimiento de Newton,
Cuando los desplazamientos son y1 e y2, el cambio en la longitud de S1 es −y1 + ∆l1 y el cambio en la longitud de S2 es −y2 + y1 + ∆l2. Ambos resortes ejercen las fuerzas de la ley de Hooke en m1, mientras que solo S2 ejerce una fuerza de la ley de Hooke en m2. Estas fuerzas están en direcciones que tienden a restaurar los resortes a su longitud natural. Por lo tanto
H1= k1(−y1 + ∆l1) − k2 (−y2 + y1 + ∆l2) y H2 = k2 (−y2 + y1 + ∆l2). (9.10.1.9)
Cuando las velocidades son y′1 y y′2, S1 y S2 cambian de longitud a las tasas −y′1 y −y′2 + y′1, respectivamente. Ambos resortes ejercen fuerzas de amortiguación sobre m1, mientras que solo S2 ejerce una fuerza de amortiguación sobre m2. Dado que la fuerza debida a la amortiguación ejercida por un resorte es proporcional a la tasa de cambio de longitud del resorte y en una dirección que se opone al cambio, se deduce que
D1 = −c1y′1 + c2 (y′2 − y′1) y D2 = −c2 (y′2 − y′1). (9.10.1.10)
De (9.10.1.8), (10.1.9) y (9.10.1.10),
y
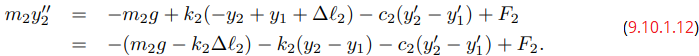
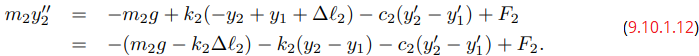
Desde (9.10.1.7),
Por lo tanto, podemos reescribir (9.10.1.11) y (9.10.1.12) como
Ejemplo ilustrativo 9.10.1_3
Sea X = X(t) = x(t) i + y(t) j + z(t) k el vector de posición en el tiempo t de un objeto con masa m, relativo a un sistema de coordenadas rectangular con origen en el centro de la Tierra (Figura 9.10.1_3).
(Figura 9.10.1_3)
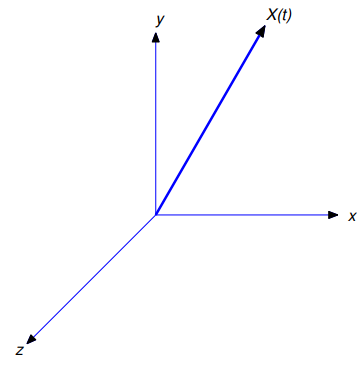
Según la ley de gravitación de Newton, la fuerza gravitacional de la Tierra F = F(x, y, z) sobre el objeto es inversamente proporcional al cuadrado de la distancia entre el objeto y el centro de la Tierra y está dirigida hacia el centro; por lo tanto,
donde K es una constante. Para determinar K, observamos que la magnitud de F es
Sea R el radio de la Tierra. Dado que ||Fk|| = mg cuando el objeto está en la superficie de la Tierra,
mg = K/R2, entonces K = mgR2.
Por lo tanto, podemos reescribir (9.10.1.13) como
Ahora suponga que F es la única fuerza que actúa sobre el objeto. Según la segunda ley del movimiento de Newton, F = mX″; es decir,
Cancelar el factor común m y equiparar componentes en los dos lados de esta ecuación produce el sistema
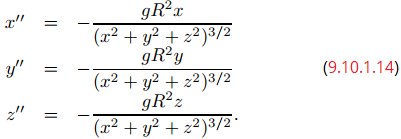
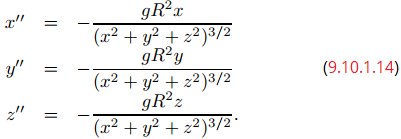
Reescritura de sistemas de orden superior como sistemas de primer orden
Un sistema de la forma
se denomina sistema de primer orden, ya que las únicas derivadas que aparecen en él son las primeras derivadas. La derivada de cada una de las incógnitas puede depender de la variable independiente y de todas las incógnitas, pero no de las derivadas de otras incógnitas. Cuando deseamos enfatizar el número de funciones desconocidas en (9.10.1.15) diremos que (9.10.1.15) es un sistema n × n.
Ejemplo ilustrativo 9.10.1_4
Reescribe el sistema
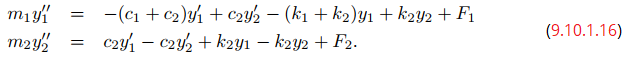
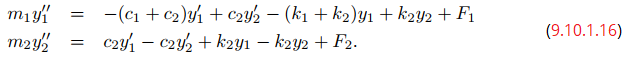
deducido en el Ejemplo 9.10.1_2 como un sistema de ecuaciones de primer orden.
Solución:
Si definimos v1 = y′1 y v2 = y′2 entonces v′1 = y″1 y v′2 = y″2, entonces (9.10.1.16) se convierte en
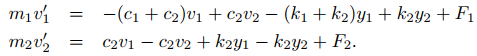
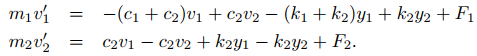
Por lo tanto, {y1, y2, v1, v2} satisface el sistema de primer orden 4 × 4
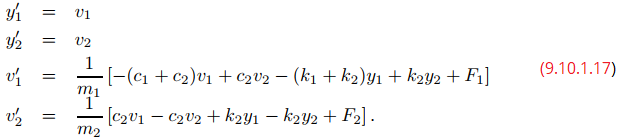
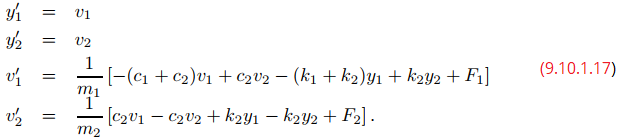
OBSERVACIÓN: La diferencia de forma entre (9.10.1.15) y (9.10.1.17), debido a la forma en que se denotan las incógnitas en los dos sistemas, no es importante; (9.10.1.17) es un sistema de primer orden, en el que cada ecuación en (9.10.1.17) expresa la primera derivada de una de las funciones desconocidas de una manera que no involucra derivadas de ninguna de las otras incógnitas.”
Ejemplo ilustrativo 9.10.1_5
Reescribe el sistema
como sistema de primer orden.
Solución:
Consideramos x, x′, y, y′ e y″ como funciones desconocidas y les cambiamos el nombre
Estas incógnitas satisfacen al sistema
Reescritura de ecuaciones diferenciales escalares como sistemas
En este capítulo nos referiremos a las ecuaciones diferenciales que involucran solo una función desconocida como ecuaciones diferenciales escalares. Las ecuaciones diferenciales escalares se pueden reescribir como sistemas de ecuaciones de primer orden mediante el método ilustrado en los dos ejemplos siguientes.
Ejemplo ilustrativo 9.10.1_6
Reescribe la ecuación
y(4) + 4y′′′+ 6y′′ + 4y′ + y = 0 (9.10.1.18)
como un sistema 4 × 4 de primer orden.
Solución:
Consideramos y, y′, y′′ e y′′′ como incógnitas y las renombramos como
y = y1, y′ = y2, y′′ = y3 y y′′′ = y4.
Entonces y(4) = y′4, entonces (9.10.1.18) se puede escribir como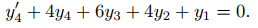
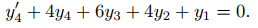
Por tanto, {y1, y2, y3, y4} satisface el sistema
Ejemplo ilustrativo 9.10.1_7
Reescribe la ecuación
como un sistema de ecuaciones de primer orden.
Solución:
Consideramos x, x′ y x′′ como incógnitas y las renombramos como
x = y1, x′ = y2 y x′′ = y3.
Entonces
y′1 = x′ = y2, y′2 = x′′ = y3 y y′3 = x′′′.
Por tanto, {y1, y2, y3} satisface el sistema de primer orden
Dado que los sistemas de ecuaciones diferenciales que implican derivadas superiores pueden reescribirse como sistemas de primer orden mediante el método utilizado en los ejemplos ilustrativos 9.10.1.5 – 9.10.1.7, consideraremos solo sistemas de primer orden.
Solución numérica de sistemas
Los métodos numéricos que estudiamos en el Capítulo 9.3 pueden extenderse a los sistemas, y la mayoría de los paquetes de software de ecuaciones diferenciales incluyen programas para resolver sistemas de ecuaciones. No entraremos en detalles sobre métodos numéricos para sistemas; sin embargo, con fines ilustrativos, describiremos el método de Runge-Kutta para la solución numérica del problema de valor inicial
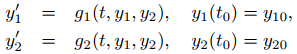
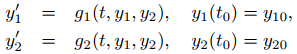
en puntos igualmente espaciados t0, t1,. . . , tn = b en un intervalo [t0, b]. Por lo tanto,
ti = t0 + ih, i = 0, 1,. . ., n,
donde
Denotaremos los valores aproximados de y1 e y2 en estos puntos por y10, y11,. . ., y1n y y20, y21,. . ., y2n.
El método de Runge-Kutta calcula estos valores aproximados de la siguiente manera: dados y1i e y2i, calcule
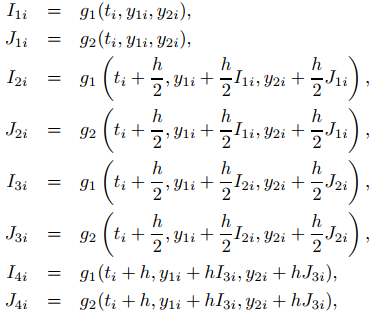
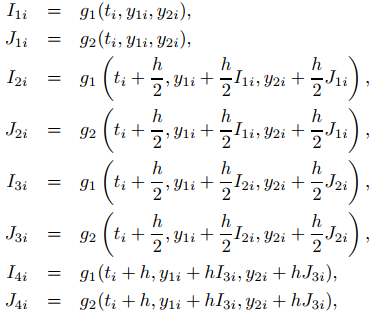
y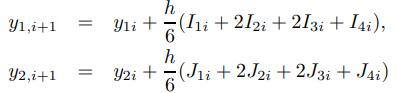
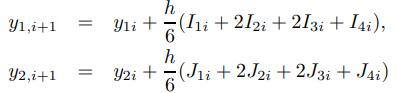
para i = 0,. . . , n − 1. En condiciones apropiadas en g1 y g2, se puede demostrar que el error de truncamiento global para el método de Runge-Kutta es O(h4), como en el caso escalar considerado en la Sección 9.3.3.