| 9. Ecuaciones diferenciales | 9.2 Ecuaciones diferenciales de primer orden |
9.2.5 Ecuaciones diferenciales exactas
En esta sección es conveniente escribir ecuaciones diferenciales de primer orden en la forma
M(x, y) dx + N(x, y) dy = 0. (9.2.5.1)
Esta ecuación se puede interpretar como


donde x es la variable independiente e y es la variable dependiente, o como


donde y es la variable independiente y x es la variable dependiente. Dado que las soluciones de (9.2.5.2) y (9.2.5.3) a menudo tendrán que dejarse en forma implícita, diremos que F(x, y) = c es una solución implícita de (9.2.5.1) si todo la función diferenciable y = y(x) que satisface F(x, y) = c es una solución de (9.2.5.2) y toda función diferenciable x = x(y) que satisface F(x, y) = c es una solución de (9.2.5.3).
Aquí hay unos ejemplos de las tres formas:


Tenga en cuenta que una ecuación separable se puede escribir en la forma (9.2.5.1) como
M(x) dx + N(y) dy = 0.
Desarrollaremos un método para resolver (9.2.5.1) bajo supuestos apropiados sobre M y N. Este método es una extensión del método de separación de variables (Ejercicio 41). Antes de enunciarlo consideremos un ejemplo.
Ejemplo ilustrativo 9.2.5_1
Muestre que
x4y3 + x2y5 + 2xy = c (9.2.5.4)
es una solución implícita de


Solución:
Considerando y como una función de x y diferenciando (9.2.5.4) implícitamente con respecto a x se obtiene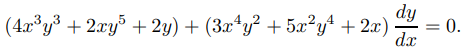
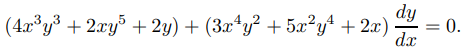
De manera similar, considerando x como una función de y y derivando (9.2.5.4) implícitamente con respecto a y se obtiene

Por tanto (9.2.5.4) es una solución implícita de (9.2.5.5) en cualquiera de sus dos posibles interpretaciones. ♦
Puede pensar que este ejemplo no tiene sentido, ya que inventar una ecuación diferencial que tiene una solución implícita dada no es particularmente interesante. Sin embargo, ilustra el siguiente teorema importante, que probaremos usando la diferenciación implícita, como en el ejemplo 9.2.5.1.
Teorema 9.2.5.1
Si F = F(x, y) tiene derivadas parciales continuas Fx y Fy, entonces
F(x, y) = c (c = constante), (9.2.5.6)
es una solución implícita de la ecuación diferencial
Fx(x, y) dx + Fy(x, y) dy = 0. (9.2.5.7) ♦
Prueba: Considerando y como una función de x y diferenciando (9.2.5.6) implícitamente con respecto a x se obtiene

Por otro lado, considerando x como una función de y y derivando (9.2.5.6) implícitamente con respecto a y se obtiene

Así, (9.2.5.6) es una solución implícita de (9.2.5.7) en cualquiera de sus dos posibles interpretaciones. ♦
Nosotros diremos que la ecuación
M(x, y) dx + N(x, y) dy = 0 (9.2.5.8)
es exacta en un rectángulo abierto R si existe una función F = F(x, y) tal que Fx y Fy son continuas, y
Fx(x, y) = M(x, y) y Fy(x, y) = N(x, y) (9.2.5.9)
para todo (x, y) en R. Este uso de “exacto” está relacionado con su uso en cálculo, donde la expresión
Fx(x, y) dx + Fy(x, y) dy
(obtenido al sustituir (9.2.5.9) en el lado izquierdo de (9.2.5.8)) es el diferencial exacto de F.
El ejemplo 9.2.5.1 muestra que es fácil resolver (9.2.5.8) si es exacta y conocemos una función F que satisface (9.2.5.9). Las preguntas importantes son:
- PREGUNTA 1. Dada una ecuación (9.2.5.8), ¿cómo podemos determinar si es exacta?
- PREGUNTA 2. Si (9.2.5.8) es exacta, ¿cómo encontramos una función F que satisfaga (9.2.5.9)?
Para descubrir la respuesta a la Pregunta 1, suponga que hay una función F que satisface (9.2.5.9) en algún rectángulo abierto R, y además que F tiene derivadas parciales mixtas continuas Fxy y Fyx. Entonces un teorema del cálculo implica que
Fxy = Fyx. (9.2.5.10)
Si Fx = M y Fy = N, derivando la primera de estas ecuaciones con respecto a y y la segunda con respecto a x se obtiene
Fxy = My y Fyx = Nx. (9.2.5.11)
De (9.2.5.10) y (9.2.5.11), concluimos que una condición necesaria para la exactitud es que My = Nx. Esto motiva el siguiente teorema, que enunciamos sin demostración.
Teorema 9.2.5.2 [La condición de exactitud]
Suponga que M y N son continuas y tienen derivadas parciales continuas My y Nx en un rectángulo abierto R. Entonces
M(x, y) dx + N(x, y) dy = 0
es exacta en R si y solo si
My(x, y) = Nx(x, y) (9.2.5.12)
para todo (x, y) en R. ♦
Para ayudarlo a recordar la condición de exactitud, observe que los coeficientes de dx y dy están diferenciados en (9.2.5.12) con respecto a las variables “opuestas”; es decir, el coeficiente de dx se diferencia con respecto a y, mientras que el coeficiente de dy se deriva con respecto a x.
Ejemplo ilustrativo 9.2.5_2
Demuestre que la ecuación
3x2y dx + 4x3 dy = 0
No es exacta en ningún rectángulo abierto.
Solución:
Aquí
M(x, y) = 3x2y y N(x, y) = 4x3
así que
My(x, y) = 3x2 y Nx(x, y) = 12x2
Por lo tanto, My = Nx en la recta x = 0, pero no en ningún rectángulo abierto, por lo que no existe una función F tal que Fx(x, y) = M(x, y) y Fy(x, y) = N(x, y) para todo (x, y) en cualquier rectángulo abierto. ♦
El siguiente ejemplo ilustra dos posibles métodos para encontrar una función F que satisfaga la condición Fx = M y Fy = N si Mdx + Ndy = 0 es exacta.
Ejemplo ilustrativo 9.2.5_3
Resolver
(4x3y3 + 3x2)dx + (3x4y2 + 6y2)dy = 0. (9.2.5.13)
Solución: (Método 1)
Aquí
M(x, y) = 4x3y3 + 3x2, N(x, y) = 3x4y2 + 6y2,
y
My(x, y) = Nx(x, y) = 12x3y2
para todo (x, y). Por lo tanto, el Teorema 9.2.5.2 implica que existe una función F tal que
Fx(x, y) = M(x, y) = 4x3y3 + 3x2 (9.2.5.14)
y
Fy(x, y) = N(x, y) = 3x4y2 + 6y2 (9.2.5.15)
para todo (x, y). Para encontrar F, integramos (9.2.5.14) con respecto a x para obtener
F(x, y) = x4y3 + x3 + φ(y), (9.2.5.16)
donde φ(y) es la “constante” de integración. (Aquí φ es “constante” en el sentido de que es independiente de x, la variable de integración). Si φ es cualquier función diferenciable de y, entonces F satisface (9.2.5.14). Para determinar φ de modo que F también satisfaga (9.2.5.15), suponga que φ es derivable y diferencie F con respecto a y. Esto produce
Fy(x, y) = 3x4y2 + φ′(y).
Comparando esto con (9.2.5.15) se observa que
φ′(y) = 6y2.
Integramos esto con respecto a y y tomamos la constante de integración como cero porque solo nos interesa encontrar alguna F que satisfaga (9.2.5.14) y (9.2.5.15). Esto produce
φ(y) = 2y3.
Sustituyendo esto en (9.2.5.16) se obtiene
F(x, y) = x4y3 + x3 + 2y3
Ahora el Teorema 9.2.5.1 implica que
x4y3 + x3 + 2y3 = c
es una solución implícita de (9.2.5.13). Resolviendo esto para y se obtiene la solución explícita

Solución: (Método 2)
En lugar de integrar primero (9.2.5.14) con respecto a x, podríamos comenzar integrando (9.2.5.15) con respecto a y para obtener
F(x, y) = x4y3 + 2y3 + ψ(x), (9.2.5.18)
donde ψ es una función arbitraria de x. Para determinar ψ, suponemos que ψ es diferenciable y derivamos F con respecto a x, lo que da como resultado
Fx(x, y) = 4x3y3 + ψ′(x).
Comparando esto con (9.2.5.14) se observa que
ψ′(x) = 3x2.
Integrando esto y tomando nuevamente la constante de integración como cero, se obtiene
ψ(x) = x3
Sustituyendo esto en (9.2.5.18) se obtiene (9.2.5.17).
La Figura 9.2.5.1 muestra un campo de direcciones y algunas curvas integrales de la ecuación (9.2.5.13),

Aquí hay un resumen del procedimiento utilizado en el Método 1 de este ejemplo. Usted debe resumir el procedimiento utilizado en el Método 2.
Procedimiento para resolver una ecuación exacta
Paso 1. Compruebe que la ecuación
M(x, y) dx + N(x, y) dy = 0 (9.2.5.19)
satisface la condición de exactitud My = Nx. Si no es así, no continúe con este procedimiento.
Paso 2. Integre


con respecto a x para obtener
F(x, y) = G(x, y) + φ(y), (9.2.5.20)
donde G es una antiderivada de M con respecto a x, y φ es una función desconocida de y.
Paso 3. Derive (9.2.5.20) con respecto a y para obtener
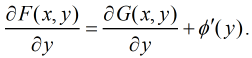
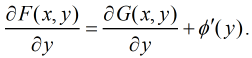
Paso 4. Iguale el lado derecho de esta ecuación a N y resuelva para φ′; por lo tanto


Paso 5. Integre φ′ con respecto a y, tomando la constante de integración igual a cero, y sustituya el resultado en (9.2.5.20) para obtener F(x, y).
Paso 6. Establezca F(x, y) = c para obtener una solución implícita de (9.2.5.19). Si es posible, resuelve y explícitamente como una función de x. ♦
Es un error común omitir el Paso 6. Sin embargo, es importante incluir este paso, ya que F no es en sí mismo una solución de (9.2.5.19).
Muchas ecuaciones pueden resolverse convenientemente mediante cualquiera de los dos métodos utilizados en el ejemplo 9.2.5.3. Sin embargo, a veces la integración requerida en un enfoque es más difícil que en el otro. En tales casos, elegimos el enfoque que requiere la integración más fácil.
Ejemplo ilustrativo 9.2.5_4
Resuelve la ecuación
(yexy tan x + exy sec2 x) dx + xexy tan x dy = 0. (9.2.5.21)
Solución:
Le dejamos a usted verificar que My = Nx en cualquier rectángulo abierto donde se definen tan x y sec x. Aquí debemos encontrar una función F tal que
Fx(x, y) = yexy tan x + exy sec2 x (9.2.5.22)
y
Fy(x, y) = xexy tan x (9.2.5.23)
Es difícil integrar (9.2.5.22) con respecto a x, pero fácil de integrar (9.2.5.23) con respecto a y. Esto produce
F(x, y) = exy tan x + ψ(x). (9.2.5.24)
Derivando esto con respecto a x se obtiene
Fx(x, y) = yexy tan x + exy sec2 x + ψ′(x).
Comparar esto con (9.2.5.22) muestra que ψ′(x) = 0. Por lo tanto, ψ es una constante, que podemos tomar como cero en (9.2.5.24), y
exy tan x = c
es una solución implícita de (9.2.5.21). ♦
Intentar aplicar nuestro procedimiento a una ecuación que no es exacta conducirá a fallar en el Paso 4, ya que la función


no será independiente de x si My ≠ Nx (Ejercicio 31), y por lo tanto no puede ser la derivada de una función de y solamente. He aquí un ejemplo que ilustra esto.
Ejemplo ilustrativo 9.2.5_5
Verifique que la ecuación
3x2y2 dx + 6x3y dy = 0 (9.2.5.25)
no es exacta, y demuestre que el procedimiento para resolver ecuaciones exactas falla cuando se aplica a (2.5.25).
Solución:
Aquí
My(x, y) = 6x2y y Nx(x, y) = 18x2y,
entonces (9.2.5.25) no es exacta. No obstante, intentemos encontrar una función F tal que
Fx(x, y) = 3x2y2 (9.2.5.26)
y
Fy(x, y) = 6x3y (9.2.5.27)
Integrando (9.2.5.26) con respecto a x se obtiene
F(x, y) = x3y2 + φ(y),
y diferenciando esto con respecto a y, se obtiene
Fy(x, y) = 2x3y + φ′(y).
Para que esta ecuación sea consistente con (9.2.5.27),
6x3y = 2x3y + φ′(y),
o
φ′(y) = 4x3y
Esto es una contradicción, ya que φ′ debe ser independiente de x. Por lo tanto, el procedimiento falla.
