| 9. Ecuaciones diferenciales | 9.4. Aplicaciones de ecuaciones de primer orden |
9.4.5 Aplicaciones a curvas
Familias de curvas de un parámetro
Comenzamos con dos ejemplos de familias de curvas generadas al variar un parámetro sobre un conjunto de números reales.
Ejemplo ilustrativo 9.4.5.1
Para cada valor del parámetro c, la ecuación
y − cx2 = 0 (9.4.5.1)
define una curva en el plano xy. Si c ≠ 0, la curva es una parábola por el origen, que se abre hacia arriba si c > 0 o hacia abajo si c < 0. Si c = 0, la curva es el eje x (Figura 9.4.5.1).
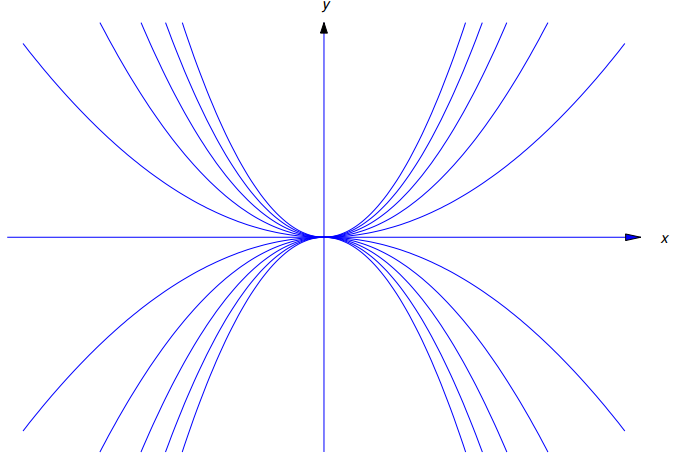

Figura 9.4.5.1 Una familia de curvas definida por y − cx2 = 0 ♦
Ejemplo ilustrativo 9.4.5.2
Para cada valor del parámetro c la ecuación
y = x + c (9.4.5.2)
define una recta con pendiente 1 (Figura 9.4.5.2).
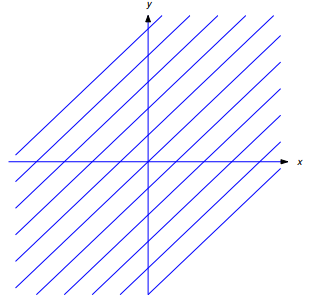

Figura 9.4.5.2 Una familia de rectas definida por y = x + c ♦
Definición 9.4.5.1
Una ecuación que se puede escribir en la forma
H(x, y, c) = 0 (9.4.5.3)
Se dice que define una familia de curvas de un parámetro si, para cada valor de c en algún conjunto no vacío de números reales, el conjunto de puntos (x, y) que satisfacen (9.4.5.3) forma una curva en el plano xy. ♦
Las ecuaciones (9.4.5.1) y (9.4.5.2) definen familias de curvas de un parámetro. (Aunque (9.4.5.2) no tiene la forma (9.4.5.3), se puede escribir de esta forma como y − x − c = 0).
Ejemplo ilustrativo 9.4.5.3
Si c > 0, la gráfica de la ecuación
x2 + y2 − c = 0 (9.4.5.4)
es una circunferencia con centro en (0, 0) y radio √c. Si c = 0, el gráfico es el punto único (0, 0). (No consideramos un solo punto como una curva). Si c < 0, la ecuación no tiene gráfica. Por lo tanto, (9.4.5.4) define una familia de curvas de un parámetro para valores positivos de c. Esta familia consta de todos las circunferencias centradas en (0, 0) (Figura 9.4.5.3).
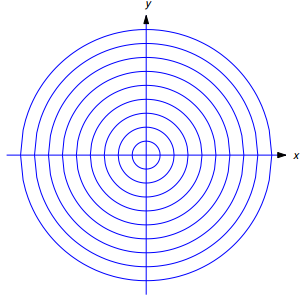

Figura 9.4.5.3 Una familia de circunferencias definida por x2 + y2 − c2 = 0 ♦
Ejemplo ilustrativo 9.4.5.4
La ecuación
x2 + y2 + c2 = 0
no define una familia de curvas de un solo parámetro, ya que ninguna (x, y) satisface la ecuación si c ≠ 0, y solo el punto único (0, 0) la satisface si c = 0. ♦
Recuerde de la Sección 9.1.2 que la gráfica de una solución de una ecuación diferencial se llama curva integral de la ecuación. Resolver una ecuación diferencial de primer orden generalmente produce una familia de curvas integrales de la ecuación de un parámetro. Aquí estamos interesados en el problema inverso: dada una familia de curvas de un parámetro, ¿existe una ecuación diferencial de primer orden para la cual cada miembro de la familia es una curva integral? Esto sugiere la siguiente definición.
Definición 9.4.5.2
Si cada curva en una familia de un parámetro definida por la ecuación
H(x, y, c) = 0 (9.4.5.5)
es una curva integral de la ecuación diferencial de primer orden
F(x, y, y′) = 0, (9.4.5.6)
entonces (9.4.5.6) se dice que es una ecuación diferencial para la familia. ♦
Para encontrar una ecuación diferencial para una familia de un parámetro, derivamos implícitamente su ecuación definitoria (9.4.5.5) con respecto a x, para obtener
Hx(x, y, c) + Hy(x, y, c)y′ = 0. (9.4.5.7)
Si esta ecuación no es así (no contiene c), entonces es una ecuación diferencial para la familia. Si contiene c, puede ser posible obtener una ecuación diferencial para la familia eliminando c entre (9.4.5.5) y (9.4.5.7).
Ejemplo ilustrativo 9.4.5.5
Encuentre una ecuación diferencial para la familia de curvas definida por
y = cx2. (9.4.5.8)
Solución:
Derivando (9.4.5.8) con respecto a x se obtiene
y′ = 2cx.
Por lo tanto, c = y′/2x, y sustituyendo esto en (9.4.5.8) se obtiene


como una ecuación diferencial para la familia de curvas definida por (9.4.5.8). La gráfica de cualquier función de la forma y = cx2 es una curva integral de esta ecuación. ♦
El siguiente ejemplo muestra que los miembros de una familia dada de curvas pueden obtenerse uniendo curvas integrales para más de una ecuación diferencial.
Ejemplo ilustrativo 9.4.5.6
(a) Trate de encontrar una ecuación diferencial para la familia de rectas tangentes a la parábola y = x2.
(b) Encuentre dos rectas tangentes a la parábola y = x2 que pasen por (2, 3), y encuentre los puntos de tangencia.
Solución:
(a) La ecuación de la recta que pasa por un punto dado (x0, y0) con pendiente m es
y = y0 + m(x − x0). (9.4.5.9)
Si (x0, y0) está en la parábola, entonces y0 = x02 y la pendiente de la recta tangente que pasa por (x0, x02) es m = 2x0; por tanto, (9.4.5.9) se convierte en
y = x02 + 2x0(x − x0),
o, de manera equivalente,
y = −x02 + 2x0x. (9.4.5.10)
Aquí x0 juega el papel de la constante c en la Definición 9.4.5.1; es decir, variar x0 sobre (−∞, ∞) produce la familia de rectas tangentes a la parábola y = x2.
Derivando (9.4.5.10) con respecto a x se obtiene y′ = 2x0. Podemos expresar x0 en términos de x e y reescribiendo (9.4.5.10) como
x02 − 2x0x + y = 0
y usando la fórmula cuadrática para obtener
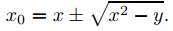
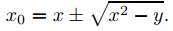
Debemos elegir el signo más en (9.4.5.11) si x < x0 y el signo menos si x > x0; de este modo,


y
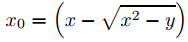
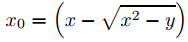
Como y′ = 2x0, esto implica que
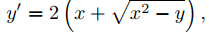
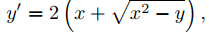
y


Ni (9.4.5.12) ni (9.4.5.13) son ecuaciones diferenciales para la familia de rectas tangentes a la parábola y = x2. Sin embargo, si se considera que cada recta tangente consta de dos semirrectas tangentes unidas en el punto de tangencia, (9.4.5.12) es una ecuación diferencial para la familia de semirrectas tangentes en las que x es menor que la abscisa del punto de tangencia (Figura 9.4.5.4(a)), mientras que (9.4.5.13) es una ecuación diferencial para la familia de semirrectas tangentes en las que x es mayor que esta abscisa (Figura 9.4.5.4(b)). La parábola y = x2 también es una curva integral de (9.4.5.12) y (9.4.5.13).
|
(a) |
(b) |
|
Figura 9.4.5.4 |
|
(b) De (9.4.5.10) el punto (x, y) = (2, 3) está en la recta tangente que pasa por (x0, x02) si y solo si
3 = −x02 + 4x0,
que es equivalente a
x02 − 4x0 + 3 = (x0 − 3)(x0 − 1) = 0.
Haciendo x0 = 3 en (9.4.5.10) muestra que (2, 3) está en la recta
y = −9 + 6x,
que es tangente a la parábola en (x0, x02) = (3, 9), como se muestra en la figura 9.4.5.5


Figura 9.4.5.5
Haciendo x0 = 1 en (9.4.5.10) muestra que (2, 3) está en la recta
y = −1 + 2x,
que es tangente a la parábola en (x0, x02) = (1, 1), como se muestra en la figura 9.4.5.5. ♦
Problemas Geométricos
Ahora consideramos algunos problemas geométricos que se pueden resolver por medio de ecuaciones diferenciales.
Ejemplo ilustrativo 9.4.5.7
Encuentre curvas y = y(x) tales que cada punto (x0, y(x0)) en la curva sea el punto medio del segmento de recta con puntos finales en los ejes de coordenadas y tangente a la curva en (x0, y(x0)) (Figura 9.4.5.6).
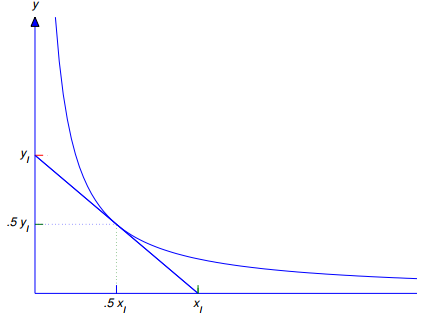

Figura 9.4.5.6
Solución:
La ecuación de la recta tangente a la curva en P = (x0, y(x0)) es
y = y(x0) + y′(x0)(x − x0).
Si denotamos las intersecciones x e y de la recta tangente por xI e yI (Figura 9.4.5.6), entonces
0 = y(x0) + y′(x0)(xI − x0) (9.4.5.14)
y
yI = y(x0) − y′(x0)x0. (9.4.5.15)
De la figura 9.4.5.6, P es el punto medio del segmento de recta que conecta (xI, 0) y (0, yI) si y solo si xI = 2x0 y yI = 2y(x0). Sustituyendo la primera de estas condiciones en (9.4.5.14) o la segunda en (9.4.5.15) se obtiene
y(x0) + y′(x0)x0 = 0.
Dado que x0 es arbitrario, eliminamos el subíndice y concluimos que y = y(x) satisface
y + xy′ = 0,
que se puede reescribir como
(xy)′ = 0.
Integrando se obtiene xy = c, o
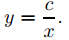
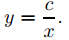
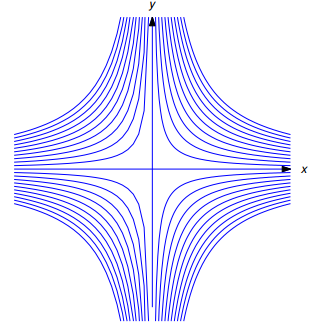
Si c = 0 esta curva es la recta y = 0, la cual no satisface los requisitos geométricos que impone el problema; así, c ≠ 0, y las soluciones definen una familia de hipérbolas (Figura 9.4.5.7).
Figura 9.4.5.7
Ejemplo ilustrativo 9.4.5.8
Encuentre curvas y = y(x) tales que la recta tangente a la curva en cualquier punto (x0, y(x0)) interseca el eje x en (x02, 0). La Figura 9.4.5.8 ilustra la situación en el caso en que la curva está en el primer cuadrante y 0 < x < 1.


Figura 9.4.5.8
Solución:
La ecuación de la recta tangente a la curva en (x0, y(x0)) es
y = y(x0) + y′(x0)(x − x0).
Como (x02, 0) está sobre la recta tangente,
0 = y(x0) + y′(x0)(x02 − x0).
Dado que x0 es arbitrario, eliminamos el subíndice y concluimos que y = y(x) satisface
y + y′(x2 − x) = 0.
Por lo tanto
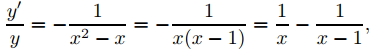
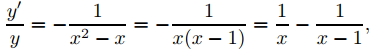
entonces


y


Si c = 0, la gráfica de esta función es el eje x. Si c ≠ 0, es una hipérbola con asíntota vertical x = 1 y asíntota horizontal y = c. La figura 9.4.5.9 muestra las gráficas para c ≠ 0. ♦
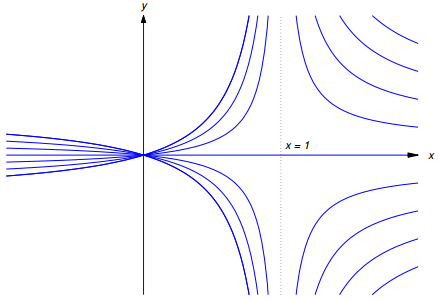

Figura 9.4.5.9
Trayectorias ortogonales
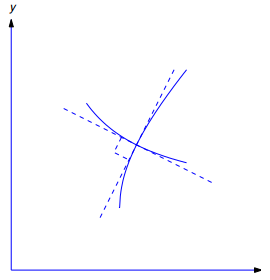
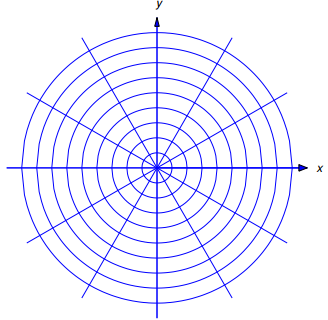
Se dice que dos curvas C1 y C2 son ortogonales en un punto de intersección (x0, y0) si tienen tangentes perpendiculares en (x0, y0). (Figura 9.4.5.10). Se dice que una curva es una trayectoria ortogonal de una familia dada de curvas si es ortogonal a todas las curvas de la familia. Por ejemplo, cada recta que pasa por el origen es una trayectoria ortogonal de la familia de circunferencias con centro en el origen. Por el contrario, cualquier circunferencia de este tipo es una trayectoria ortogonal de la familia de rectas a través del origen (Figura 9.4.5.11).
|
Figura 9.4.5.10 Curvas ortogonales en un punto de intersección |
Figura 9.4.5.11 Familias ortogonales de circunferencias y rectas |
Las trayectorias ortogonales ocurren en muchas aplicaciones físicas. Por ejemplo, si u = u(x, y) es la temperatura en un punto (x, y), las curvas definidas por
u(x, y) = c (9.4.5.16)
se llaman curvas isotérmicas. Las trayectorias ortogonales de esta familia se denominan líneas de flujo de calor, porque en cualquier punto dado la dirección del flujo de calor máximo es perpendicular a la isotérmica que pasa por el punto. Si u representa la energía potencial de un objeto que se mueve bajo una fuerza que depende de (x, y), las curvas (9.4.5.16) se llaman equipotenciales y las trayectorias ortogonales se llaman líneas de fuerza.
De la geometría analítica sabemos que dos rectas no verticales L1 y L2 con pendientes m1 y m2, respectivamente, son perpendiculares si y sólo si m2 = −1/m2; por lo tanto, las curvas integrales de la ecuación diferencial
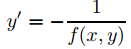
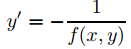
son trayectorias ortogonales de las curvas integrales de la ecuación diferencial
y′ = f (x, y),
porque en cualquier punto (x0, y0) donde las curvas de las dos familias se cruzan, las pendientes de las respectivas rectas tangentes son
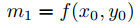
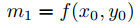
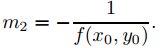
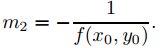
Esto sugiere un método para encontrar trayectorias ortogonales de una familia de curvas integrales de una ecuación de primer orden.
Encontrar trayectorias ortogonales
Paso 1. Encuentra una ecuación diferencial
y′ = f (x, y)
para la familia dada.
Paso 2. Resuelve la ecuación diferencial


para encontrar las trayectorias ortogonales. ♦
Ejemplo ilustrativo 9.4.5.9
Encuentre las trayectorias ortogonales de la familia de circunferencias
x2 + y2 = c2 (c > 0). (9.4.5.17)
Solución:
Para encontrar una ecuación diferencial para la familia de circunferencias derivamos (9.4.5.17) implícitamente con respecto a x para obtener
2x + 2yy′ = 0,
o
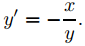
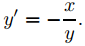
Por lo tanto, las curvas integrales de


son trayectorias ortogonales de la familia dada. Te dejamos comprobar que la solución general de esta ecuación es
y = kx,
donde k es una constante arbitraria. Esta es la ecuación de una recta no vertical que pasa por (0, 0). El eje y también es una trayectoria ortogonal de la familia dada. Por lo tanto, cada recta que pasa por el origen es una trayectoria ortogonal de la familia dada (9.4.5.17) (Figura 9.4.5.11). Esto es consistente con el teorema de la geometría plana que establece que el diámetro de un círculo y una recta tangente al círculo al final del diámetro son perpendiculares. ♦
Ejemplo ilustrativo 9.4.5.10
Encuentre las trayectorias ortogonales de la familia de hipérbolas
xy = c (c ≠ 0) (9.4.5.18)
Solución:
Derivando (9.4.5.18) implícitamente con respecto a x, se obtiene
y + xy′ = 0,
o


por lo tanto, las curvas integrales de


son trayectorias ortogonales de la familia dada. Separando variables, obtenemos
y’y = x
e integrando, se obtiene
y2 − x2 = k,
que es la ecuación de una hipérbola si k ≠ 0, o de las rectas y = x e y = −x si k = 0 (Figura 9.4.5.12). ♦


Figura 9.4.5.12 Trayectorias ortogonales de las hipérbolas xy = c.
Ejemplo ilustrativo 9.4.5.10
Encuentre las trayectorias ortogonales de la familia de circunferencias definida por
(x − c)2 + y2 = c2 (c ≠ 0). (9.4.5.19)
Estas circunferencias están centrados en el eje x y son tangentes al eje y (Figura 9.4.5.13(a)).
|
Figura 9.4.5.13 (a) Las circunferencias (x − c)2 + y2 = c2 |
(b) Las circunferencias x2 + (y − h)2 = h2 |
Solución:
Desarrollando y simplificando (9.4.5.19) se obtiene
x2 − 2cx + y2 = 0, (9.4.5.20)
y diferenciando esto implícitamente con respecto a x se obtiene
2(x − c) + 2yy′ = 0. (9.4.5.21)
De (9.4.5.20),


entonces
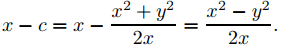
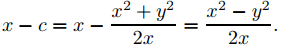
Sustituyendo esto en (9.4.5.21) y resolviendo para y′ se obtiene


Las curvas definidas por (9.4.5.19) son curvas integrales de (9.4.5.22), y las curvas integrales de
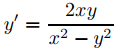
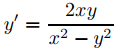
son trayectorias ortogonales de la familia (9.4.5.19). Esta es una ecuación no lineal homogénea, que estudiamos en la Sección 9.2.4. Sustituyendo y = ux obtenemos
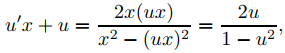
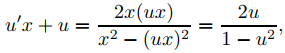
entonces


Separando variables, obtenemos


o, de manera equivalente,
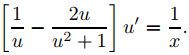
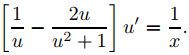
Por lo tanto
ln|u| − ln(u2 + 1) = ln|x| + k.
Sustituyendo u = y/x, vemos que
ln|y| − ln|x| − ln(x2 + y2) + ln(x2) = ln|x| + k,
que, dado que ln(x2) = 2 ln|x|, es equivalente a
ln|y| − ln(x2 + y2) = k,
o
|y| = ek(x2 + y2).
Para ver cuáles son estas curvas, reescribimos esta ecuación como


y completa el cuadrado para obtener
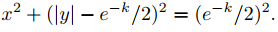
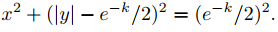
Esto se puede reescribir como
x2 + (y − h)2 = h2,
donde


Así, las trayectorias ortogonales son circunferencias centradas en el eje y y tangentes al eje x (Figura 9.4.5.13(b)). Las circunferencias para las que h > 0 están por encima del eje x, mientras que aquellos para los que h < 0 están por debajo.