LA REGLA DE L’HÔPITAL: Objetivos de aprendizaje
4.8.1. Reconocer cuándo aplicar la regla de L’Hôpital.
4.8.2. Identificar formas indeterminadas producidas por cocientes, productos, sustracciones y potencias, y aplicar la regla de L’Hôpital en cada caso.
4.8.3. Describir las tasas de crecimiento relativo de las funciones.
En esta sección, examinamos una herramienta poderosa para evaluar límites. Esta herramienta, conocida como la regla de L’Hôpital, utiliza derivadas para calcular los límites. Con esta regla, podremos evaluar muchos límites que aún no hemos podido determinar. En lugar de confiar en la evidencia numérica para conjeturar que existe un límite, podremos demostrar definitivamente que existe un límite y determinar su valor exacto.
Aplicando la regla de L’Hôpital
La regla de L’Hôpital se puede utilizar para evaluar los límites que involucran el cociente de dos funciones. Consideremos el siguiente límite








Llamamos a esta una de las formas indeterminadas, del tipo 0/0. Esto se considera una forma indeterminada porque no podemos determinar el comportamiento exacto de f (x) / g (x) cuando x → a sin un análisis adicional. Hemos visto ejemplos de esto anteriormente en el texto. Por ejemplo, considere


Para el primero de estos ejemplos, podemos evaluar el límite factorizando el numerador y escribiendo


Para el segundo ejemplo podemos mostrar, usando un argumento geométrico, que


Aquí usamos una técnica diferente para evaluar límites como estos. Esta técnica no solo proporciona una manera más fácil de evaluar estos límites, sino que también, y lo que es más importante, nos brinda una forma de evaluar muchos otros límites que no pudimos calcular previamente.
La idea detrás de la regla de L’Hôpital se puede explicar usando aproximaciones lineales locales. Considere dos funciones diferenciables f y g tales que


y con g′(a) ≠ 0.
Para x cerca de a, podemos escribir
f (x) ≈ f (a) + f ′ (a) (x − a) y g (x) ≈ g (a) + g ′ (a) (x − a).
Por lo tanto,




Como f es diferenciable en a, entonces f es continua en a, y por lo tanto f (a) = limx → a f(x) = 0.
Del mismo modo, g (a) = lim x → a g(x) = 0.
Si también suponemos que f ′ y g ′ son continuas en x = a, entonces f ′ (a) = lim x → a f ′ (x) y g ′ (a) = lim x → a g ′ (x). Usando estas ideas, concluimos que


Tenga en cuenta que las condiciones de que f ′ y g ′ sean continuas en a y g ′ (a) ≠ 0 pueden aflojarse. Establecemos formalmente la regla de L’Hôpital para la forma indeterminada 0/0. También tenga en cuenta que la notación 0/0 no significa que en realidad estamos dividiendo cero por cero. Más bien, estamos usando la notación 0/0 para representar un cociente de límites, cada uno de los cuales es cero.
Teorema 4..8.1. Regla de L’Hôpital (caso 0/0)
Suponga que f y g son funciones diferenciables en un intervalo abierto que contiene a a, excepto posiblemente en a. Si limx → a f (x) = 0 y limx → a g(x) = 0, entonces
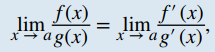
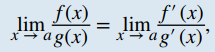
suponiendo que el límite a la derecha existe o es ∞ o −∞. Este resultado también se cumple si estamos considerando límites unilaterales, o si a = ∞ y − ∞.
Prueba
Proporcionamos una prueba de este teorema en el caso especial cuando f, g, f ‘ y g‘ son todas continuas en un intervalo abierto que contiene a. En ese caso, dado que limx → a f (x) = 0 = limx → a g (x) y f y g son continuas en a, se deduce que f (a) = 0 = g (a). Por lo tanto,


Tenga en cuenta que la regla de L’Hôpital establece que podemos calcular el límite de un cociente f /g considerando el límite del cociente de las derivadas f ′/g′. Es importante darse cuenta de que no estamos calculando la derivada del cociente f /g.

supongamos que sabemos que f'(x) es una función continua. Use la regla de Lhopital para mostrar que:
log_(x→0)〖(f(x+h)-f(x-h))/2h〗=f'(x)