ECUACIONES PARAMÉTRICAS Y COORDENADAS POLARES
Área y longitud de arco en coordenadas polares: Objetivos de aprendizaje
8.4.1. Aplica la fórmula para el área de una región en coordenadas polares.
8.4.2. Determine la longitud de arco de una curva polar.
En el sistema de coordenadas rectangulares, la integral definida proporciona una forma de calcular el área bajo una curva. En particular, si tenemos una función y = f (x) definida desde x = a hasta x = b donde f (x) > 0 en este intervalo, el área entre la curva y el eje x viene dada por


Este hecho, junto con la fórmula para evaluar esta integral, se resume en el Teorema Fundamental del Cálculo. De manera similar, la longitud del arco de esta curva está dada por


En esta sección, estudiamos fórmulas análogas para el área y la longitud del arco en el sistema de coordenadas polares.
Áreas de regiones limitadas por curvas polares
Hemos estudiado las fórmulas para el área bajo una curva definida en coordenadas rectangulares y curvas definidas paramétricamente. Ahora enfocamos nuestra atención en deducir una fórmula para el área de una región limitada por una curva polar. Recuerde que la demostración del Teorema fundamental del cálculo utilizó el concepto de una suma de Riemann para aproximar el área bajo una curva usando rectángulos. Para las curvas polares, usamos la suma de Riemann nuevamente, pero los rectángulos se reemplazan por sectores de un círculo.
Considere una curva definida por la función r = f (θ), donde α ≤ θ ≤ β. Nuestro primer paso es dividir el intervalo [α, β] en n subintervalos de igual ancho. El ancho de cada subintervalo viene dado por la fórmula Δθ = (β − α)/n, y el i-ésimo punto de partición θᵢ está dado por la fórmula θᵢ = α + iΔθ. Cada punto de partición θ = θᵢ define una línea con pendiente tanθᵢ que pasa a través del polo como se muestra en el siguiente gráfico.

Los segmentos de recta están conectados por arcos de radio constante. Define sectores cuyas áreas se pueden calcular mediante una fórmula geométrica. El área de cada sector se usa luego para aproximar el área entre segmentos de recta sucesivos. Luego sumamos las áreas de los sectores para aproximar el área total. Este enfoque proporciona una aproximación de sumas de Riemann para el área total. La fórmula para el área de un sector de un círculo se ilustra en la siguiente figura.


Recuerda que el área de un círculo es A = πr². Al medir ángulos en radianes, 360 grados es igual a 2π radianes. Por lo tanto, una fracción de un círculo se puede medir con el ángulo central θ. La fracción del círculo está dada por θ/2π, por lo que el área del sector es esta fracción multiplicada por el área total:


Dado que el radio de un sector típico en la figura 8.4_1 está dado por rᵢ = f (θᵢ), el área del i-ésimo sector está dada por


Por lo tanto, una suma de Riemann que se aproxima al área está dada por


Tomamos el límite cuando n → ∞ para obtener el área exacta:
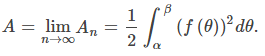
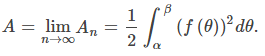
Lo anterior se resume en el siguiente teorema.
TEOREMA 8.4.1 Área de una región limitada por una curva polar
|
Suponga que f es una función continua y no negativa en el intervalo α ≤ θ ≤ β con 0 < β − α ≤ 2π. El área de la región delimitada por la gráfica de r = f (θ) entre las líneas radiales θ = α y θ = β es
|
Ejemplo ilustrativo 8.4_1 Encontrar un área de una región polar
Encuentre el área de un pétalo de la rosa definida por la ecuación r = 3sen(2θ).
Solución:
A continuación se muestra la gráfica de r = 3sen(2θ).


Cuando θ = 0 tenemos r = 3sen(2(0)) = 0. El siguiente valor para el cual r = 0 es θ = π/2. Esto se puede ver resolviendo la ecuación 3sen(2θ) = 0 para θ. Por lo tanto, los valores θ = 0 a θ = π/2 trazan el primer pétalo de la rosa. Para encontrar el área dentro de este pétalo, use la ecuación dada en el Teorema 8.4.1 con f (θ) = 3sen(2θ), α = 0 y β = π/2:


Para evaluar esta integral, use la fórmula sen2α = (1 − cos(2α))/2 con α = 2θ:


Ejercicio de control 8.4_1
Encuentre el área dentro del cardioide definida por la ecuación r = 1 − cosθ.
El ejemplo 8.4_1 implicó encontrar el área dentro de una curva. También podemos usar el Área de una región limitada por una curva polar para encontrar el área entre dos curvas polares. Sin embargo, a menudo necesitamos encontrar los puntos de intersección de las curvas y determinar qué función define la curva exterior o la curva interior entre estos dos puntos.
Ejemplo ilustrativo 8.4_2 Encontrar el área entre dos curvas polares
Encuentre el área fuera del cardioide r = 2 + 2senθ y dentro del círculo r = 6senθ.
Solución:
Primero dibuje un gráfico que contenga ambas curvas como se muestra a continuación


Para determinar los límites de integración, primero encuentre los puntos de intersección igualando las dos funciones entre sí y despejando θ:
6senθ = 2 + 2senθ
4senθ = 2
senθ = 1/2.
Esto da las soluciones θ = π/6 y θ = 5π/6, que son los límites de integración. El círculo r = 3senθ es el gráfico rojo, que es la función externa, y el cardioide r = 2 + 2senθ es el gráfico azul, que es la función interna. Para calcular el área entre las curvas, comience con el área dentro del círculo entre θ = π/6 y θ = 5π/6, luego reste el área dentro del cardioide entre θ = π/6 y θ = 5π/6:
A = círculo − cardioide
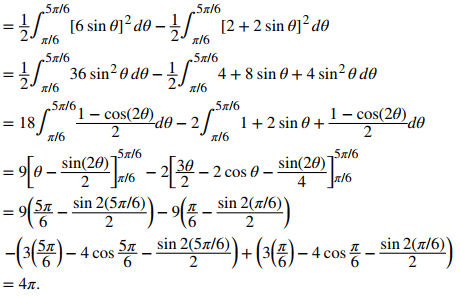
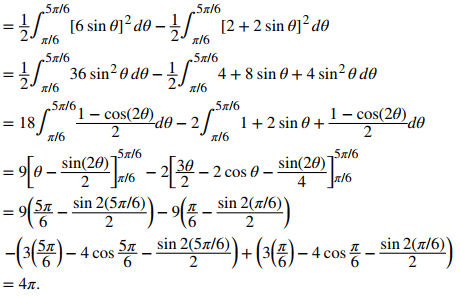
Ejercicio de control 8.4_2
Encuentra el área dentro del círculo r = 4cosθ y fuera del círculo r = 2.
En el ejemplo 8.4_2, encontramos el área dentro del círculo y fuera del cardioide al encontrar primero sus puntos de intersección. Observe que al resolver la ecuación directamente para θ se obtienen dos soluciones: θ = π/6 y θ = 5π/6. Sin embargo, en el gráfico hay tres puntos de intersección. El tercer punto de intersección es el origen. La razón por la que este punto no apareció como una solución es porque el origen está en ambos gráficos pero para diferentes valores de θ. Por ejemplo, para el cardioide obtenemos
2 + 2senθ = 0
senθ = −1,
entonces los valores de θ que resuelven esta ecuación son θ = 3π/2 + 2nπ, donde n es cualquier número entero. Por el círculo obtenemos
6senθ = 0.
Las soluciones de esta ecuación son de la forma θ = nπ para cualquier valor entero de n. Estos dos conjuntos de soluciones no tienen puntos en común. Independientemente de este hecho, las curvas se cruzan en el origen. Este caso siempre debe tenerse en cuenta.

