| 10. Cálculo vectorial – Vectores en el espacio | Ejercicios propuestos para el Capítulo 10.8 |
10.8 Funciones vectoriales y curvas espaciales
Objetivos de aprendizaje:
10.8.1. Escribir la ecuación general de una función de valor vectorial en forma de componente y en forma de vector unitario.
10.8.2. Reconocer las ecuaciones paramétricas de una curva en el espacio.
10.8.3. Describir la forma de una hélice y escribir su ecuación.
10.8.4. Definir el límite de una función de valor vectorial.
Nuestro estudio de las funciones de valores vectoriales combina las ideas de nuestro análisis del cálculo de una sola variable con nuestra descripción de los vectores en tres dimensiones del capítulo anterior. En esta sección ampliamos conceptos de capítulos anteriores y también examinamos nuevas ideas relativas a las curvas en el espacio tridimensional. Estas definiciones y teoremas apoyan la presentación del material en el resto de este capítulo y también en los capítulos restantes del texto.
Definición de una función vectorial
El primer paso en el estudio del cálculo de funciones de valores vectoriales es definir qué es exactamente una función de valor vectorial. A continuación, podemos observar gráficos de las funciones de valores vectoriales y ver cómo definen las curvas en dos y tres dimensiones.
Definición 10.8.1: Función de valores vectoriales
Una función de valor vectorial es una función de la forma
\[ \mathbf{r}(t) = f(t) \mathbf{i} + g(t) \mathbf{j} \quad \text{o} \quad \mathbf{r}(t) = f(t) \mathbf{i} + g(t) \mathbf{j} + h(t) \mathbf{k}, \hspace{20pt} \text{(Ecuación 10.8.1)} \]donde las funciones componentes \(f\), \(g\), y \(h\), son funciones de valor real del parámetro \(t\). Las funciones de valores vectoriales también se escriben en la forma
\[ \mathbf{r}(t) = \langle f(t), g(t) \rangle \quad \text{o} \quad \mathbf{r}(t) = \langle f(t), g(t), h(t) \rangle. \hspace{20pt} \text{(Ecuación 10.8.2)} \]En ambos casos, la primera forma de la función define una función con valores vectoriales bidimensional; la segunda forma describe una función con valores vectoriales tridimensional. ♦
El parámetro t puede estar entre dos números reales: a ≤ t ≤ b. Otra posibilidad es que el valor de t pueda tomar todos los números reales. Por último, las funciones de los componentes pueden tener restricciones de dominio que imponen restricciones sobre el valor de t. A menudo usamos t como parámetro porque t puede representar el tiempo.
Ejemplo ilustrativo 10.8_1. Evaluación de funciones vectoriales y determinación de dominios
Para cada una de las siguientes funciones de valores vectoriales, evalúe r (0), r (π/2) y r (2π/3). ¿Alguna de estas funciones tiene restricciones de dominio?
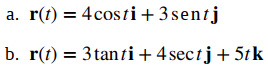
Solución:
a. Para calcular cada uno de los valores de la función, sustituya el valor correspondiente de t en la función:

Para determinar si esta función tiene restricciones de dominio, considere las funciones de los componentes por separado. La función del primer componente es f (t) = 4cost y la función del segundo componente es g (t) = 3sent. Ninguna de estas funciones tiene una restricción de dominio, por lo que el dominio de r (t) = 4cost i + 3sent j son todos números reales.
b. Para calcular cada uno de los valores de la función, sustituya el valor apropiado de t en la función:

Para determinar si esta función tiene restricciones de dominio, considere las funciones de los componentes por separado. La función del primer componente es f (t) = 3tant, la función del segundo componente es g (t) = 4sect, y la función del tercer componente es h (t) = 5t. Las dos primeras funciones no están definidas para múltiplos impares de π / 2, por lo que la función no está definida para múltiplos impares de π / 2. Por lo tanto,
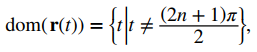
donde n es cualquier número entero. ♦
Ejercicio de control 10.8.1
Para la función con valores vectoriales \(\mathbf{r}(t) = (t^2 – 3t) \mathbf{i} + (4t + 1) \mathbf{j}\), evalúe \(\mathbf{r}(0)\), \(\mathbf{r}(1)\), y \(\mathbf{r}(-4)\).
¿Tiene esta función alguna restricción de dominio? ♦
El ejemplo anterior ilustra un concepto importante. El dominio de una función vectorial está formado por números reales. El dominio puede ser todos los números reales o un subconjunto de los números reales. El rango de una función vectorial está formado por vectores. Cada número real en el dominio de una función vectorial se asigna a un vector bidimensional o tridimensional.
Representación gráfica de funciones vectoriales
Recuerde que un vector en el plano consta de dos cantidades: dirección y magnitud. Dado cualquier punto en el plano (el punto inicial), si nos movemos en una dirección específica para una distancia específica, llegamos a un segundo punto. Esto representa el punto terminal del vector. Calculamos los componentes del vector restando las coordenadas del punto inicial de las coordenadas del punto terminal.
Se considera que un vector está en posición estándar si el punto inicial se encuentra en el origen. Al graficar una función con valor vectorial, generalmente graficamos los vectores en el dominio de la función en posición estándar, porque hacerlo garantiza la unicidad del gráfico. Esta convención se aplica también a los gráficos de las funciones de valores vectoriales tridimensionales. La gráfica de una función vectorial de la forma r (t) = f (t) i + g (t) j consiste en el conjunto de todos los (t, r(t)), y la ruta que traza se llama curva plana. La gráfica de una función de valor vectorial de la forma r(t) = f (t) i + g (t) j + h (t) k consiste en el conjunto de todos los (t, r(t)), y la trayectoria que traza se llama curva espacial. Cualquier representación de una curva plana o una curva espacial usando una función vectorial se llama parametrización vectorial de la curva.
Ejemplo ilustrativo 10.8_2. Graficar una función vectorial
Cree una gráfica de cada una de las siguientes funciones con valores vectoriales:
a. La curva plana representada por r(t) = 4cost i + 3sent j, 0 ≤ t ≤ 2π
b. La curva plana representada por r(t) = 4cost3 i + 3sent3 j, 0 ≤ t ≤ 2π
c. La curva espacial representada por r(t) = cost i + sent j + tk, 0 ≤ t ≤ 4π
Solución:
a. Como con cualquier gráfica, comenzamos con una tabla de valores. Luego graficamos cada uno de los vectores en la segunda columna de la tabla en la posición estándar y conectamos los puntos terminales de cada vector para formar una curva (Figura 10.8_1). Esta curva resulta ser una elipse centrada en el origen.
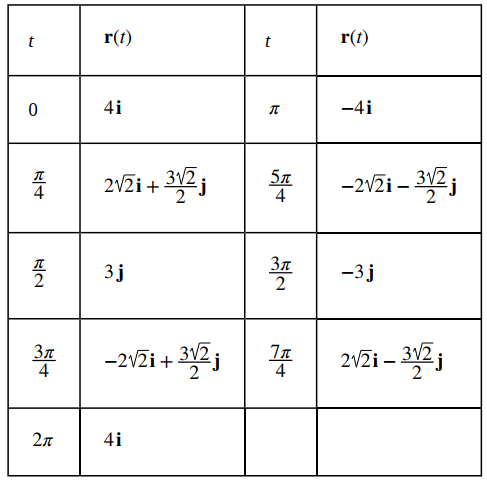
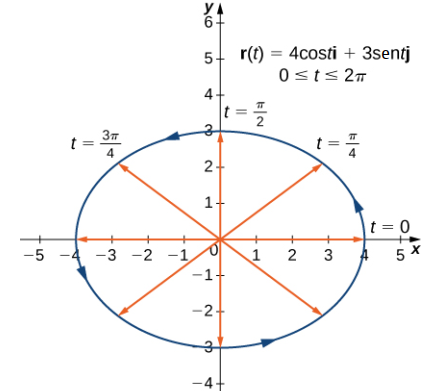
b. La tabla de valores para r(t) = 4cost i + 3sint j, 0 ≤ t ≤ 2π es la siguiente:
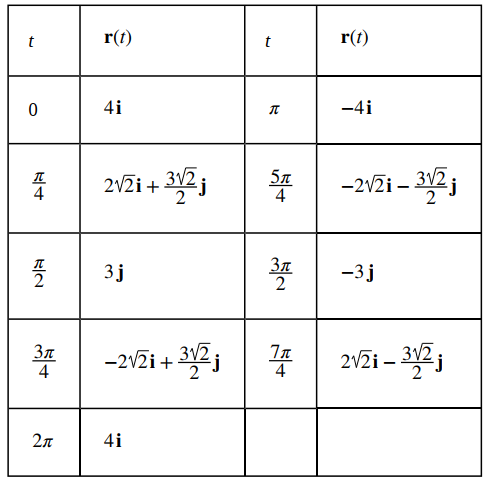
La gráfica de esta curva también es una elipse centrada en el origen.

c. Pasamos por el mismo procedimiento para trazar la gráfica una función vectorial tridimensional.

Los valores luego se repiten, excepto por el hecho de que el coeficiente de k siempre aumenta (Figura 10.8_3). Esta curva se llama hélice. Observe que si se elimina el componente k, la función se convierte en r(t) = cost i + sint j, que es una circunferencia unitaria centrada en el origen.
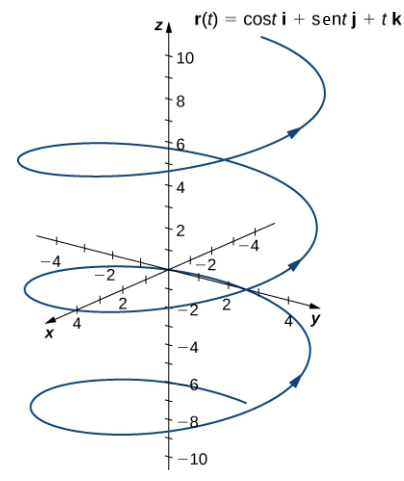
♦
Puede notar que las gráficas en las partes a. y b. son idénticas. Esto sucede porque la función que describe la curva b. es una llamada reparametrización de la función que describe la curva a. De hecho, cualquier curva tiene un número infinito de reparametrizaciones; por ejemplo, podemos reemplazar t con 2t en cualquiera de las tres curvas anteriores sin cambiar la forma de la curva. El intervalo sobre el cual se define t puede cambiar, pero eso es todo. Volvemos a esta idea más adelante en este capítulo cuando estudiamos la parametrización de longitud de arco.
Como se mencionó, el nombre de la forma de la curva de la gráfica en el ejemplo 10.8_3.c. es una hélice (figura 10.8_3). La curva se asemeja a un resorte, con una sección transversal circular que mira hacia abajo a lo largo del eje z. Es posible que una hélice sea también elíptica en sección transversal. Por ejemplo, la función de valor vectorial r(t) = 4cost i + 3sent j + tk describe una hélice elíptica. La proyección de esta hélice en el plano xy es una elipse. Por último, las flechas en el gráfico de esta hélice indican la orientación de la curva a medida que t progresa de 0 a 4π.
Ejercicio de control 10.8.2
Cree una gráfica de la función con valores vectoriales \(\mathbf{r}(t) = (t^2 – 1) \mathbf{i} + (2t – 3) \mathbf{j}\), \(0 \leq t \leq 3\). ♦
En este punto, puede notar una similitud entre las funciones de valor vectorial y las curvas parametrizadas. De hecho, dada una función de valor vectorial r(t) = f (t) i + g (t) j, podemos definir x = f (t) e y = g (t). Si existe una restricción en los valores de t (por ejemplo, t está restringido al intervalo [a, b] para algunas constantes a < b), entonces esta restricción se aplica al parámetro. La gráfica de la función parametrizada estaría de acuerdo con la gráfica de la función con valor vectorial, excepto que la gráfica con valor vectorial representaría vectores en lugar de puntos. Como podemos parametrizar una curva definida por una función y = f (x), también es posible representar una curva plana arbitraria mediante una función vectorial.
Límites y continuidad de una función vectorial
Ahora echamos un vistazo al límite de una función vectorial. Es importante entender esto para estudiar el cálculo de las funciones con valores vectoriales.
Definición 10.8.2: Límite de una función vectorial
\[ \lim_{t \to a} \mathbf{r}(t) = \mathbf{L}, \]siempre que
\[ \lim_{t \to a} ||\mathbf{r}(t) – \mathbf{L}|| = 0. \]♦
Esta es una definición rigurosa del límite de una función vectorial. En la práctica, utilizamos el siguiente teorema:
Teorema 10.8.1: Límite de una función vectorial
Sean \(f\), \(g\), y \(h\) funciones de \(t\). Entonces el límite de la función con valores vectoriales \(\mathbf{r}(t) = f(t) \mathbf{i} + g(t) \mathbf{j}\) cuando \(t\) se acerca a \(a\) está dado por
\[ \lim_{t \to a} \mathbf{r}(t) = \left[ \lim_{t \to a} f(t) \right] \mathbf{i} + \left[ \lim_{t \to a} g(t) \right] \mathbf{j}, \hspace{20pt} \text{(Ecuación 10.8.3)} \]siempre que los límites \(\lim_{t \to a} f(t)\) y \(\lim_{t \to a} g(t)\) existan. De manera similar, el límite de la función con valores vectoriales \(\mathbf{r}(t) = f(t) \mathbf{i} + g(t) \mathbf{j} + h(t) \mathbf{k}\) cuando \(t\) se acerca a \(a\) está dado por
\[ \lim_{t \to a} \mathbf{r}(t) = \left[ \lim_{t \to a} f(t) \right] \mathbf{i} + \left[ \lim_{t \to a} g(t) \right] \mathbf{j} + \left[ \lim_{t \to a} h(t) \right] \mathbf{k}, \hspace{20pt} \text{(Ecuación 10.8.4)} \]siempre que los límites \(\lim_{t \to a} f(t)\), \(\lim_{t \to a} g(t)\) y \(\lim_{t \to a} h(t)\) existan. ♦
En el siguiente ejemplo, mostramos cómo calcular el límite de una función vectorial.
Ejemplo ilustrativo 10.8_3. Evaluación del límite de una función vectorial
Para cada una de las siguientes funciones vectoriales, calcule limt → 3 r (t) para
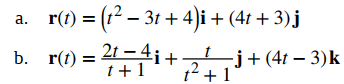
Solución:
a. Use la primera ecuación del Teorema 10.8.1 y sustituya el valor t = 3 en las dos expresiones componentes:
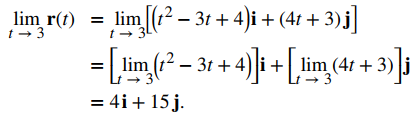
b. Use la segunda ecuación del Teorema 10.8.1 y sustituya el valor t = 3 en las dos expresiones componentes:
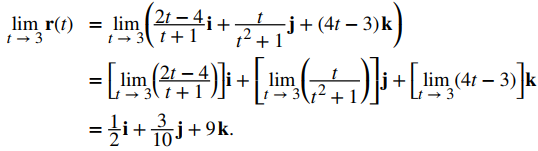
♦
Ejercicio de control 10.8.23
Calcule \(\displaystyle \lim_{t \to -2} \mathbf{r}(t)\) para la función \(\mathbf{r}(t) = \sqrt{t^2 – 3t – 1} \mathbf{i} + (4t + 3) \mathbf{j} + \sin \frac{(t + 1)\pi}{2} \mathbf{k}\). ♦
Ahora que sabemos cómo calcular el límite de una función vectorial, podemos definir la continuidad en un punto para dicha función.
Definición 10.8.3: Continuidad de una función vectorial en un punto
Sean \(f\), \(g\), y \(h\) funciones de \(t\). Entonces, la función con valores vectoriales \(\mathbf{r}(t) = f(t) \mathbf{i} + g(t) \mathbf{j}\) es continua en el punto \(t = a\) si se cumplen las siguientes tres condiciones:
- \(\mathbf{r}(a)\) existe
- \(\lim_{t \to a} \mathbf{r}(t)\) existe
- \(\lim_{t \to a} \mathbf{r}(t) = \mathbf{r}(a)\)
De manera similar, la función con valores vectoriales \(\mathbf{r}(t) = f(t) \mathbf{i} + g(t) \mathbf{j} + h(t) \mathbf{k}\) es continua en el punto \(t = a\) si se cumplen las siguientes tres condiciones:
- \(\mathbf{r}(a)\) existe
- \(\lim_{t \to a} \mathbf{r}(t)\) existe
- \(\lim_{t \to a} \mathbf{r}(t) = \mathbf{r}(a)\)
♦

¡Hola! ¿Alguien tiene conocimiento sobre si crean complementos para protegerse contra los piratas informáticos? Estoy un poco paranoico por perder todo lo que he trabajado duro. ¿Alguna recomendación?
Great content! Super high-quality! Keep it up! 🙂