| 9. Ecuaciones diferenciales |

9.3. Métodos numéricos: Objetivos de aprendizaje

       En este capítulo estudiamos métodos numéricos para resolver una ecuación diferencial de primer orden.

La SECCIÓN 9.3.1 trata del método de Euler, que en realidad es demasiado tosco para ser de mucha utilidad en aplicaciones prácticas. Sin embargo, su simplicidad permite una introducción a las ideas necesarias para comprender los mejores métodos discutidos en las otras dos secciones.
La SECCIÓN 9.3.2 analiza las mejoras en el método de Euler.
La SECCIÓN 9.3.3 trata del método de Runge-Kutta, quizás el método más utilizado para la solución numérica de ecuaciones diferenciales.

9.3.1 MÉTODO DE EULER

Si un problema de valor inicial

y′ = f (x, y),  y(x₀) = y₀        (9.3.1.1)

no se puede resolver analíticamente, es necesario recurrir a métodos numéricos para obtener aproximaciones útiles a una solución de (9.3.1.1). Consideraremos estos métodos en este capítulo.

        Estamos interesados en calcular valores aproximados de la solución de (9.3.1.1) en puntos igualmente espaciados x₀, x₁,. . . , x_n = b en un intervalo [x₀, b]. Por lo tanto,

x_i = x₀ + ih, i = 0, 1, . . ., n,

donde

Denotaremos los valores aproximados de la solución en estos puntos por y₀, y₁,. . . , y_n; por tanto, y_i es una aproximación de y(x_i). Llamaremos

e_i = y(x_i) − y_i

el error en el i-ésimo paso. Debido a la condición inicial y(x₀) = y₀, siempre tendremos e₀ = 0. Sin embargo, en general e_i ≠ 0 si i > 0.

       Encontramos dos fuentes de error al aplicar un método numérico para resolver un problema de valor inicial:
• Las fórmulas que definen el método se basan en algún tipo de aproximación. Los errores debidos a la inexactitud de la aproximación se denominan errores de truncamiento.
• Las computadoras hacen aritmética con un número fijo de dígitos y, por lo tanto, cometen errores al evaluar las fórmulas que definen los métodos numéricos. Los errores debidos a la incapacidad de la computadora para realizar operaciones aritméticas exactas se denominan errores de redondeo.
       Dado que un análisis cuidadoso del error de redondeo está más allá del alcance de este libro, consideraremos solo los errores de truncamiento.

Método de Euler

El método numérico más simple para resolver (9.3.1.1) es el método de Euler. Este método es tan tosco que rara vez se utiliza en la práctica; sin embargo, su simplicidad lo hace útil con fines ilustrativos.

      El método de Euler se basa en el supuesto de que la recta tangente a la curva integral de (9.3.1.1) en (x_i, y(x_i)) se aproxima a la curva integral en el intervalo [x_i, x_{i + 1}]. Dado que la pendiente de la curva integral de (9.3.1.1) en (x_i, y(x_i)) es y′(x_i) = f (x_i, y(x_i)), la ecuación de la recta tangente a la curva integral en (x_i, y(x_i)) es

y = y(x_i) + f (x_i, y(x_i)) (x − x_i).        (9.3.1.2)

Al establecer x = x_{i + 1} = x_i + h en (9.3.1.2) se obtiene

y_{i + 1} = y(x_i) + h f (x_i, y(x_i))        (9.3.1.3)

como una aproximación a y(x_{i + 1}). Como se conoce y(x₀) = y₀, podemos usar (9.3.1.3) con i = 0 para calcular

y₁ = y₀ + h f (x₀, y₀).

Sin embargo, al establecer i = 1 en (9.3.1.3) se obtiene

y₂ = y(x₁) + h f (x₁, y(x₁)),

lo cual no es útil, ya que no sabemos el valor de y(x₁). Por lo tanto, reemplazamos y(x₁) por su valor aproximado y₁ y redefinimos

y₂ = y₁ + h f (x₁, y₁).

Habiendo calculado y₂, podemos calcular

y₃ = y₂ + h f (x₂, y₂).

En general, el método de Euler comienza con el valor conocido y(x₀) = y₀ y calcula y₁, y₂,. . . , y_n sucesivamente con la fórmula

y_{i + 1} = y_i + h f (x_i, y_i),  0 ≤ i ≤ n − 1.      (9.3.1.4)

    El siguiente ejemplo ilustra el procedimiento de cálculo indicado en el método de Euler.

Ejemplo ilustrativo 9.3.1.1

Use el método de Euler con h = 0.1 para encontrar valores aproximados para la solución del problema de valor inicial

       (9.3.1.5)

en x = 0.1, 0.2, 0.3.

Solución:

Reescribimos (9.3.1.5) como

que es de la forma (9.3.1.1), con

aplicando el método de Euler, se obtiene

      Hemos escrito los detalles de estos cálculos para asegurarnos de que comprenda el procedimiento. Sin embargo, en el resto de los ejemplos, así como en los ejercicios de este capítulo, asumiremos que puede utilizar una calculadora programable o una computadora para realizar los cálculos necesarios.

Ejemplos que ilustran el error en el método de Euler

Ejemplo ilustrativo 9.3.1.2

Utilice el método de Euler con tamaños de paso h = 0.1, h = 0.05 y h = 0.025 para encontrar valores aproximados de la solución del problema de valor inicial.en x = 0, 0,1, 0,2, 0,3,. . . , 1.0. Compare estos valores aproximados con los valores de la solución exacta

        (9.3.1.6) 

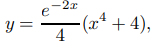
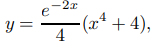
que se puede obtener mediante el método de la Sección 9.2.1. (Verificar)

Solución:

La tabla 9.3.1.1 muestra los valores de la solución exacta (9.3.1.6) en los puntos especificados y los valores aproximados de la solución en estos puntos obtenidos por el método de Euler con tamaños de paso h = 0.1, h = 0.05 y h = 0.025 . Al examinar esta tabla, tenga en cuenta que los valores aproximados en la columna correspondiente a h = .05 son en realidad los resultados de 20 pasos con el método de Euler. No hemos enumerado las estimaciones de la solución obtenida para x = 0.05, 0.15,. . . , ya que no hay nada con qué compararlos en la columna correspondiente a h = 0.1. De manera similar, los valores aproximados en la columna correspondiente a h = 0.025 son en realidad los resultados de 40 pasos con el método de Euler.

(Tabla 9.3.1.1. Solución numérica de y′ + 2y = x³e ^{− 2x}, y(0) = 1, por el método de Euler.)

Puede ver en la tabla 9.3.1.1 que disminuir el tamaño del paso mejora la precisión del método de Euler.
Por ejemplo,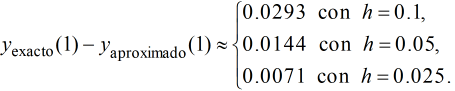

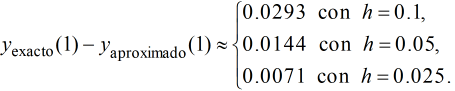
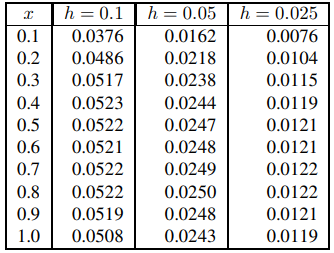
Con base en esta escasa evidencia, podría adivinar que el error al aproximar la solución exacta a un valor fijo de x por el método de Euler se reduce aproximadamente a la mitad cuando el tamaño del paso se reduce a la mitad. Puede encontrar más evidencia para apoyar esta conjetura examinando la tabla 9.3.1.2, que enumera los valores aproximados de y_exacto − y_aproximado en x = 0.1, 0.2,. . . , 1.0.

(Tabla 9.3.1.2. Errores en soluciones aproximadas de y′ + 2y = x³e ^{− 2x}, y(0) = 1, obtenido por el método de Euler.)

Ejemplo ilustrativo 9.3.1.3

Las tablas 9.3.1.3 y 9.3.1.4 muestran resultados análogos para el problema de valor inicial no lineal

y′ = −2y² + xy + x²,  y(0) = 1,        (9.3.1.7)

excepto que en este caso no podemos resolver (9.3.1.7) exactamente. Los resultados en la columna “Exacto” se obtuvieron utilizando un método numérico más preciso conocido como el método de Runge-Kutta con un tamaño de paso pequeño. Son exactos a ocho lugares decimales. 

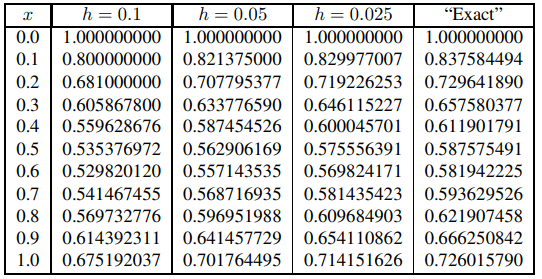
      Dado que creemos que es importante para evaluar la precisión de los métodos numéricos que estudiaremos en este capítulo, a menudo incluimos una columna que enumera los valores de la solución exacta del problema de valor inicial, incluso si las instrucciones del ejemplo o del ejercicio no lo piden específicamente. Si se incluyen comillas en el encabezado, los valores se obtuvieron aplicando el método de Runge-Kutta de la manera que se explica en la Sección 9.3.3. Si no se incluyen las comillas, los valores se obtuvieron de una fórmula conocida para la solución. En cualquier caso, los valores son exactos hasta ocho lugares a la derecha del punto decimal.

Error de truncamiento en el método de Euler

De acuerdo con los resultados indicados en las tablas 9.3.1.1 a 9.3.1.4, ahora mostraremos que, bajo supuestos razonables sobre f, existe una constante K tal que el error al aproximar la solución del problema de valor inicial

y′ = f(x, y), y(x₀) = y₀,

en un punto dado b > x₀ por el método de Euler con tamaño de paso h = (b − x₀)/n satisface la desigualdad

|y(b) − y_n| ≤ Kh,

donde K es una constante independiente de n.

 

       Hay dos fuentes de error (sin contar el redondeo) en el método de Euler:

1. El error cometido al aproximar la curva integral por la recta tangente y = y(x_i) + f (x_i, y(x_i)) (x − x_i) (9.3.1.2) sobre el intervalo [x_i, x_i+1].

2. El error cometido al reemplazar y(x_i) por y_i en (9.3.1.2) y usar y_{i + 1} = y_i + h f (x_i, y_i),  0 ≤ i ≤ n − 1 (9.3.1.4) en lugar de (9.3.1.2) para calcular y_i+1.

 

      El método de Euler asume que y_i+1 definido en (9.3.1.2) es una aproximación a y(x_i+1). Llamamos al error en esta aproximación el error de truncamiento local en el i-ésimo paso, y lo denotamos por T_i; por lo tanto,

T_i = y(x_i+1) − y(x_i) − hf(x_i, y(x_i)).      (9.3.1.8)

Ahora usaremos el teorema de Taylor para estimar T_i, asumiendo por simplicidad que f, f_x y f_y son continuas y acotadas para todo (x, y). Entonces y″ existe y está acotado en [x₀, b]. Para ver esto, diferenciamos

y′(x) = f(x, y(x))

para obtener

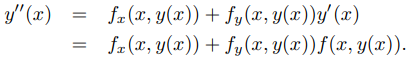
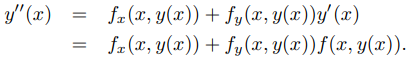
Como asumimos que f, f_x y f_y están acotadas, existe una constante M tal que

lo que implica que

y″(x)| ≤ M, x₀ < x < b.        (9.3.1.9)

Dado que x_i+1 = x_i + h, el teorema de Taylor implica que

donde es un número entre x_i y x_i+1. Dado que y′(x_i) = f(x_i, y(x_i)) esto se puede escribir como

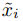
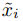
o equivalente,

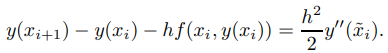
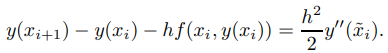
Comparando esto con (9.3.1.8) se observa que

Recordando (9.3.1.9), podemos establecer el límite

       (9.3.1.10)

Aunque puede ser difícil determinar la constante M, lo importante es que existe una M tal que (9.3.1.10) se cumple. Decimos que el error de truncamiento local del método de Euler es de orden h², que escribimos como O(h²).

      Tenga en cuenta que la magnitud del error de truncamiento local en el método de Euler está determinada por la segunda derivada y″ de la solución del problema de valor inicial. Por lo tanto, el error de truncamiento local será mayor donde |y″| es grande, o menor donde |y″| es pequeño.

      Dado que el error de truncamiento local para el método de Euler es O(h²), es razonable esperar que reducir a la mitad h reduzca el error de truncamiento local en un factor de 4. Esto es cierto, pero reducir a la mitad el tamaño del paso también requiere el doble de pasos para aproximar el solución en un punto dado. Para analizar el efecto general del error de truncamiento en el método de Euler, es útil derivar una ecuación que relacione los errores

e_i+1 = y(x_i+1) − y_i+1  y  e_i = y(x_i) − y_i.

Para ello, recuerda que

      (9.3.1.11)

y

      (9.3.1.12)

Restando (9.3.1.12) de (9.3.1.11) se obtiene

       (9.3.1.13)

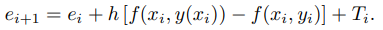
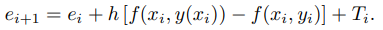
El último término de la derecha es el error de truncamiento local en el i-ésimo paso. Los otros términos reflejan la forma en que los errores cometidos en los pasos anteriores afectan a e_i+1. Desde |T_i| ≤ Mh²/2, vemos de (9.3.1.13) que

      (9.3.1.14)

Como asumimos que f_y es continua y acotada, el teorema del valor medio implica que

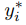
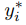
dondeestá entre y_i y y(x_i). Por lo tanto

para alguna R constante. De esto y (9.3.1.14),

      (9.3.1.15)

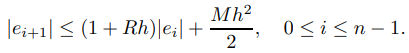
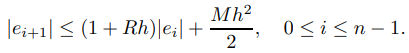
Por conveniencia, sea C = 1 + Rh. Como e₀ = y(x₀) − y₀ = 0, aplicando (9.3.1.15) repetidamente se obtiene

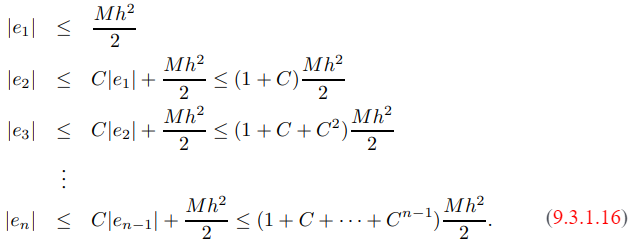
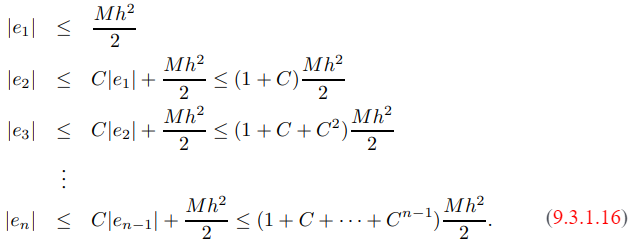
Recordando la fórmula para la suma de una serie geométrica, vemos que

(ya que C = 1 + Rh). De esto y (9.3.1.16),

          (9.3.1.17)

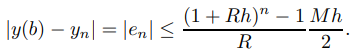
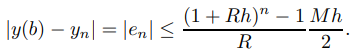
Dado que el teorema de Taylor implica que

1 + Rh < e^Rh

(verificar),

Esto y (9.3.1.17) implican que

y(b) − y_n| ≤ Kh,         (9.3.1.18)

con

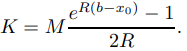
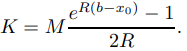
Por (9.3.1.18) decimos que el error de truncamiento global del método de Euler es de orden h, que escribimos como O(h).

Ecuaciones Semilineales y Variación de Parámetros

Una ecuación que se puede escribir en la forma

y′ + p(x)y = h(x, y)         (9.3.1.19)

con p0 se dice que es semilineal. (Por supuesto, (9.3.1.19) es lineal si h es independiente de y). Una forma de aplicar el método de Euler a un problema de valor inicial

y′ + p(x)y = h(x, y), y(x₀) = y₀        (9.3.1.20)

para (9.3.1.19) es pensar en ello como

y′ = f(x, y), y(x₀) = y₀,

donde

f(x, y) = −p(x)y + h(x, y).

Sin embargo, también podemos comenzar aplicando variación de parámetros a (9.3.1.20), como en las Secciones 9.2.1 y 9.2.4; por lo tanto, escribimos la solución de (9.3.1.20) como y = uy₁, donde y₁ es una solución no trivial de la ecuación complementaria y′ + p(x)y = 0. Entonces y = y = uy₁ es una solución de (9.3.1.20) si y solo si u es una solución del problema de valor inicial

u′ = h(x, uy₁(x))/y₁(x), u(x₀) = y(x₀)/y₁(x₀).         (9.3.1.21)

Podemos aplicar el método de Euler para obtener valores aproximados u₀, u₁, . . . , u_n de este problema de valor inicial, y luego tomar

y_i = u_iy₁(x_i)

como valores aproximados de la solución de (9.3.1.20). Llamaremos a este procedimiento el método semilineal de Euler.

 

      Los siguientes dos ejemplos muestran que los métodos semilineales de Euler y Euler pueden arrojar resultados drásticamente diferentes.

 

Ejemplo ilustrativo 9.3.1.4

En el Ejemplo 9.2.1.7 tuvimos que dejar la solución del problema de valor inicial

y′ − 2xy = 1, y(0) = 3        (9.3.1.22)

en la forma

        (9.3.1.23)

porque era imposible evaluar esta integral exactamente en términos de funciones elementales. Use tamaños de paso h = 0.2, h = 0.1 y h = 0.05 para encontrar valores aproximados de la solución de (9.3.1.22) en x = 0, 0.2, 0.4, 0.6, . . . , 2.0 por (a) el método de Euler; (b) el método semilineal de Euler.

Solución:

(a) Reescribiendo (9.3.1.22) como

y′ = 1 + 2xy, y(0) = 3        (9.3.1.24)

y aplicando el método de Euler con f(x, y) = 1 + 2xy se obtienen los resultados que se muestran en la tabla 9.3.1.5. Debido a las grandes diferencias entre las estimaciones obtenidas para los tres valores de h, sería evidente que estos resultados son inútiles incluso si los valores “exactos” no se incluyeran en la tabla.

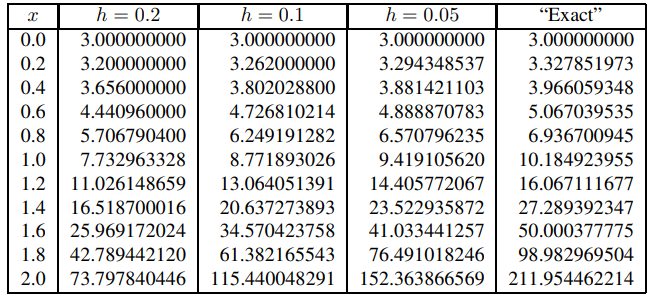
Es fácil ver por qué el método de Euler produce resultados tan pobres. Recuerde que la constante M en (9.3.1.10) – que juega un papel importante en la determinación del error de truncamiento local en el método de Euler –  debe ser un límite superior para los valores de la segunda derivada y″ de la solución del problema de valor inicial (9.3.1.22) en (0, 2). El problema es que y″ asume valores muy grandes en este intervalo. Para ver esto derivamos (9.3.1.24) para obtener

y″(x) = 2y(x) + 2xy′(x) = 2y(x) + 2x(1 + 2xy(x)) = 2(1 + 2x²)y(x) + 2x

donde la segunda igualdad sigue de nuevo de (9.3.1.24). Dado que (9.3.1.23) implica que 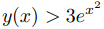si x > 0,

Por ejemplo, haciendo que x = 2 muestra que y″(2) > 2952.

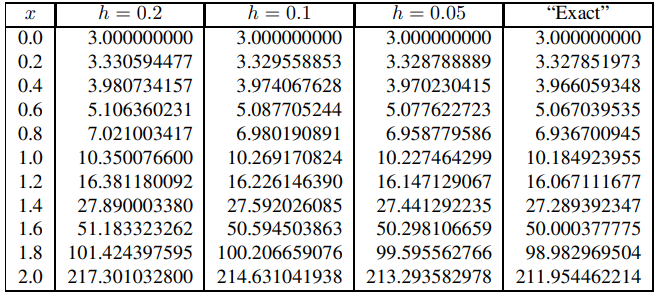
(b) Como  es una solución de la ecuación complementaria y′ − 2xy = 0, podemos aplicar el método semilineal de Euler a (9.3.1.22), con

Los resultados enumerados en la Tabla 9.3.1.6 son claramente mejores que los obtenidos por el método de Euler.

      No podemos dar un procedimiento general para determinar de antemano si el método de Euler o el método semilineal de Euler producirán mejores resultados para un problema de valor inicial semilineal dado y′ + p(x)y = h(x, y), y(x₀) = y₀ (9.3.1.20). Como regla general, el método semilineal de Euler dará mejores resultados que el método de Euler si |u″| es pequeño en [x₀, b], mientras que el método de Euler da mejores resultados si |u″| es grande en [x₀, b]. En muchos casos los resultados obtenidos por los dos métodos no difieren apreciablemente. Sin embargo, proponemos una forma intuitiva de decidir cuál es el mejor método: probar ambos métodos con varios tamaños de paso, como hicimos en el Ejemplo 9.3.1.4, y aceptar los resultados obtenidos por el método para el que las aproximaciones cambian menos a medida que disminuye el tamaño del paso.

Ejemplo ilustrativo 9.3.1.5

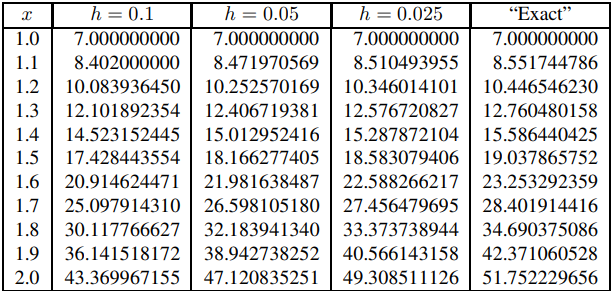
Aplicar el método de Euler con tamaños de paso h = 0.1, h = 0.05 y h = 0.025 al problema de valor inicial

      (9.3.1.25)

en [1, 2] arroja los resultados de la Tabla 9.3.1.7. Aplicando el método semilineal de Euler con

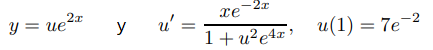
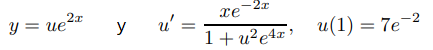
da los resultados de la Tabla 9.3.1.8. Dado que estos últimos son claramente menos dependientes del tamaño del paso que los primeros, concluimos que el método semilineal de Euler es mejor que el método de Euler para (9.3.1.25). Esta conclusión se sustenta comparando los resultados aproximados obtenidos por los dos métodos con los valores “exactos” de la solución.

Ejemplo ilustrativo 9.3.1.6

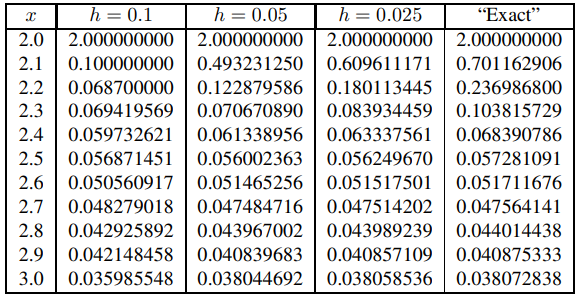
Aplicar el método de Euler con tamaños de paso h = 0.1, h = 0.05 y h = 0.025 al problema de valor inicial

y′ + 3x²y = 1 + y²,  y(2) = 2        (9.3.1.26)

en [2, 3] arroja los resultados de la Tabla 9.3.1.9. Aplicando el método semilineal de Euler con

da los resultados de la Tabla 9.3.1.10. Observando la estrecha concordancia entre las tres columnas de la Tabla 9.3.1.9 (al menos para valores mayores de x) y la falta de dicha concordancia entre las columnas de la Tabla 9.3.1.10, concluimos que el método de Euler es mejor que el método semilineal de Euler. para (9.3.1.26). La comparación de los resultados con los valores exactos apoya esta conclusión.

      En las próximas dos secciones estudiaremos otros métodos numéricos para resolver problemas de valor inicial, llamados el método mejorado de Euler, el método del punto medio, el método de Heun y el método de Runge-Kutta. Si el problema de valor inicial es semilineal como en (9.3.1.19), también tenemos la opción de usar la variación de parámetros y luego aplicar el método numérico dado al problema de valor inicial (9.3.1.21) para u. Por analogía con la terminología utilizada aquí, llamaremos al procedimiento resultante método semilineal de Euler mejorado, método semilineal del punto medio, método semilineal de Heun o método semilineal de Runge-Kutta, según sea el caso.