| 7. Sucesiones y series infinitas |
SERIES INFINITAS: Objetivos de aprendizaje
7.2.1. Explicar el significado de la suma de una serie infinita.
7.2.2. Calcular la suma de una serie geométrica.
7.2.3. Evaluar una serie telescópica.
Hemos visto que una sucesión es un conjunto ordenado de términos. Si suma estos términos juntos, obtendrá una serie. En esta sección definimos una serie infinita y mostramos cómo las series están relacionadas con las sucesiones. También definimos lo que significa que una serie converja o diverja. Presentamos uno de los tipos de series más importantes: las series geométricas. Usaremos series geométricas en el próximo capítulo para escribir ciertas funciones como polinomios con un número infinito de términos. Este proceso es importante porque nos permite evaluar, diferenciar e integrar funciones complicadas mediante el uso de polinomios que son más fáciles de manejar. También discutimos la serie armónica, posiblemente la serie divergente más interesante porque simplemente no converge.
Sumas y series
Una serie infinita es una suma de infinitos términos y está escrita en la forma


Pero ¿qué significa esto? No podemos sumar un número infinito de términos de la misma manera que podemos sumar un número finito de términos. En cambio, el valor de una serie infinita se define en términos del límite de sumas parciales. Una suma parcial de una serie infinita es una suma finita de la forma
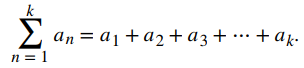
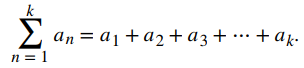
Para ver cómo usamos sumas parciales para evaluar series infinitas, considere el siguiente ejemplo. Suponga que el petróleo se está filtrando en un lago de manera que 1000 galones ingresen al lago la primera semana. Durante la segunda semana, 500 galones adicionales de petróleo ingresan al lago. La tercera semana, 250 galones más ingresan al lago. Suponga que este patrón continúa de tal manera que cada semana la mitad del petróleo ingresa al lago como lo hizo la semana anterior. Si esto continúa para siempre, ¿qué podemos decir sobre la cantidad de petróleo en el lago? ¿La cantidad de petróleo continuará aumentando arbitrariamente o es posible que se acerque a una cantidad finita? Para responder a esta pregunta, observamos la cantidad de petróleo en el lago después de k semanas. Dejando que Sk denote la cantidad de petróleo en el lago (medido en miles de galones) después de k semanas, vemos que
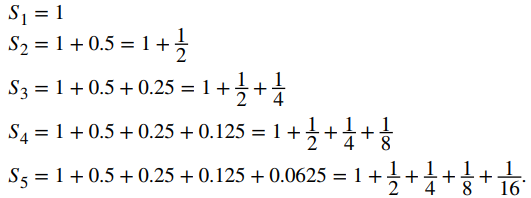
Al observar este patrón, vemos que la cantidad de petróleo en el lago (en miles de galones) después de k semanas es
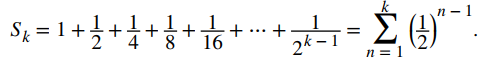
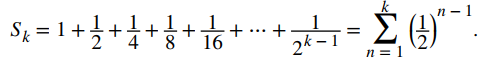
Estamos interesados en lo que sucede cuando k → ∞. Simbólicamente, la cantidad de petróleo en el lago cuando k → ∞ viene dada por la serie infinita


Al mismo tiempo, cuando k → ∞, la cantidad de petróleo en el lago se puede calcular evaluando limk → ∞Sk. Por lo tanto, el comportamiento de las series infinitas se puede determinar observando el comportamiento de la sucesión de sumas parciales {Sk}. Si la sucesión de sumas parciales {Sk} converge, decimos que la serie infinita converge, y su suma está dada por limk → ∞Sk. Si la sucesión {Sk} diverge, decimos que la serie infinita diverge. Ahora dirigimos nuestra atención a determinar el límite de esta sucesión {Sk}.
Primero, simplificando algunas de estas sumas parciales, vemos que


Al trazar algunos de estos valores en el plano, observe la Figura 7.2.1, parece que la sucesión {Sk} podría estar aproximándose a 2.


(Figura 7.2.1 La gráfica muestra la sucesión de sumas parciales {Sk}. Parece que la sucesión se aproxima al valor 2.)
Busquemos evidencia más convincente. En la siguiente tabla, mostramos los valores de Sk para varios valores de k.
| k | 5 | 10 | 15 | 20 |
| Sk | 1.9375 | 1.998 | 1.999939 | 1.999998 |
Estos datos proporcionan más evidencia que sugiere que la sucesión {Sk} converge a 2. Más adelante proporcionaremos un argumento analítico que puede usarse para demostrar que limk → ∞Sk = 2. Por ahora, confiamos en los datos numéricos y gráficos para convencernos de que la sucesión de sumas parciales realmente converge a 2. Dado que esta sucesión de sumas parciales converge a 2, decimos que la serie infinita converge a 2 y escribimos


Volviendo a la pregunta sobre el petróleo en el lago, dado que esta serie infinita converge a 2, concluimos que la cantidad de petróleo en el lago se acercará arbitrariamente a 2000 galones a medida que la cantidad de tiempo sea lo suficientemente grande.
Esta serie es un ejemplo de una serie geométrica. Abordaremos las series geométricas con mayor detalle más adelante en esta sección. Primero, resumimos lo que significa que una serie infinita converja.
Definición 7.2.1. Serie infinita
Una serie infinita es una expresión de la forma


Para cada entero positivo k, la suma


se llama la suma parcial k de la serie infinita. Las sumas parciales forman una secuencia {Sk}. Si la sucesión de sumas parciales converge a un número real S, la serie infinita converge. Si podemos establecer la convergencia de una serie a S, llamamos a S la suma de la serie, y escribimos


Si la sucesión de sumas parciales diverge, tenemos una serie divergente. ◆
Tenga en cuenta que el índice para una serie no necesita comenzar con n = 1 sino que puede comenzar con cualquier otro valor. Por ejemplo, la serie


también se puede escribir como


A menudo es conveniente que el índice comience en 1, por lo que si por alguna razón comienza en un valor diferente, podemos reindexar haciendo un cambio de variables. Por ejemplo, considere la serie


Al introducir la variable m = n − 1, de modo que n = m + 1, podemos reescribir la serie como


EJEMPLO ILUSTRATIVO 7.2_1. Evaluación de límites de secuencias de sumas parciales
Para cada una de las siguientes series, use la secuencia de sumas parciales para determinar si la serie converge o diverge.
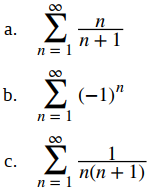
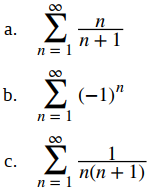
Solución:
a. La secuencia de sumas parciales {Sk} satisface


Tenga en cuenta que cada término agregado es mayor que 1/2. Como resultado, vemos que
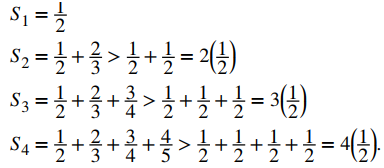
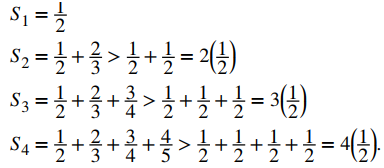
De este patrón podemos ver que Sk > k(1/2) para cada entero k. Por lo tanto, {Sk} no tiene límites y, en consecuencia, diverge. Por lo tanto, la serie infinita.


diverge.
b. La secuencia de sumas parciales {Sk} satisface


A partir de este patrón podemos ver que la secuencia de sumas parciales es


Como esta secuencia diverge, la serie infinita


Diverge.
c. La secuencia de sumas parciales {Sk} satisface
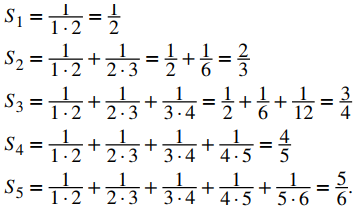
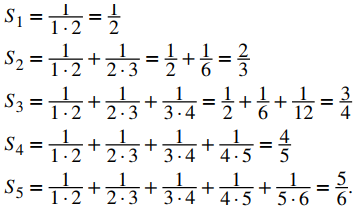
A partir de este patrón, podemos ver que la suma parcial enésima está dada por la fórmula explícita


Como k/(k + 1) → 1, concluimos que la secuencia de sumas parciales converge y, por lo tanto, la serie infinita converge a 1. Tenemos
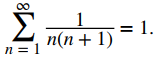
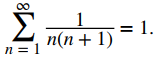
Ejercicio de control 7.2.1
Determine si la serie 


PEDRO PABLO MONTOYA: ACÁ ESTÁ MI COMENTARIO.