La divergencia y la prueba de la integral

LA DIVERGENCIA Y LA PRUEBA DE LA INTEGRAL: Objetivos de aprendizaje

5.3.1. Usar la prueba de la divergencia para determinar si una serie converge o diverge.
5.3.2. Usar la prueba de la integral para determinar la convergencia de una serie.
5.3.3. Estimar el valor de una serie encontrando límites en el término restante.

En la sección anterior, determinamos la convergencia o divergencia de varias series calculando explícitamente el límite de la sucesión de sumas parciales {S_k}. En la práctica, calcular explícitamente este límite puede ser difícil o imposible. Afortunadamente, existen varias pruebas que nos permiten determinar la convergencia o divergencia para muchos tipos de series. En esta sección, discutimos dos de estas pruebas: la prueba de la divergencia y la prueba de la integral. Examinaremos varias otras pruebas en el resto de este capítulo y luego resumiremos cómo y cuándo usarlas.

Prueba de la divergencia

Para que una serie

converja, el enésimo término a_n debe satisfacer a_n → 0 como n → ∞.

Observemos que a partir de las propiedades algebraicas de límites para sucesiones,

Por lo tanto, si

converge, el enésimo término a_n → 0 cuando n → ∞. Una consecuencia importante de este hecho es la siguiente afirmación:

Esta prueba se conoce como la prueba de la divergencia porque proporciona una forma de demostrar que una serie diverge.

Teorema 7.3_1.  Prueba de la divergencia

---

Es importante tener en cuenta que lo contrario de este teorema no es cierto. Es decir, si lim_{n → ∞}a_n = 0, no podemos hacer ninguna conclusión sobre la convergencia de

Por ejemplo, lim_{n → ∞}a_n (1/n) = 0, pero la serie armónica

diverge.

En esta sección y en las secciones restantes de este capítulo, mostramos muchos más ejemplos de tales series. En consecuencia, aunque podemos usar la prueba de divergencia para mostrar que una serie diverge, no podemos usarla para demostrar que una serie converge. Específicamente, si a_n → 0, la prueba de divergencia no es concluyente.

EJEMPLO ILUSTRATIVO 7.3_1. Usando la prueba de divergencia

Para cada una de las siguientes series, aplique la prueba de divergencia. Si la prueba de divergencia prueba que la serie diverge, indíquelo. De lo contrario, indique que la prueba de divergencia no es concluyente.

Solución:
a. Dado que n / (3n − 1) → 1/3 ≠ 0, mediante la prueba de divergencia, podemos concluir que

b. Como 1 / n³ → 0, la prueba de divergencia no es concluyente.

c. Dado que

por la prueba de divergencia, la serie

diverge.

Prueba de la integral

En la sección anterior, demostramos que la serie armónica diverge mirando la sucesión de sumas parciales {S_k} y mostrando que S_2^k > 1 + k / 2 para todos los enteros positivos k. En esta sección usamos una técnica diferente para probar la divergencia de las series armónicas. Esta técnica es importante porque se utiliza para demostrar la divergencia o convergencia de muchas otras series. Esta prueba, llamada prueba de la integral, compara una suma infinita con una integral impropia. Es importante tener en cuenta que esta prueba solo se puede aplicar cuando consideramos una serie cuyos términos son todos positivos.

Para ilustrar cómo funciona la prueba de la integral, usaremos la serie armónica como ejemplo. En la figura 7.3_1, representamos la serie armónica dibujando una secuencia de rectángulos con áreas 1, 1/2, 1/3, 1/4, … junto con la función f(x) = 1/x. De la gráfica, vemos que

Por lo tanto, para cada k, la k-ésima suma parcial S_k satisface

Como lim_{k → ∞}ln(k + 1) = ∞, vemos que la sucesión de sumas parciales {S_k} no tiene límites. Por lo tanto, {S_k} diverge y, en consecuencia, la serie

también diverge.

(Figura 7.3_1  La suma de las áreas de los rectángulos es mayor que el área entre la curva f(x) = 1/x y el eje x para x ≥ 1. Como el área delimitada por la curva es infinita (calculada por una integral impropia), la suma de las áreas de los rectángulos también es infinita.)

Ahora considera la serie

Mostramos cómo se puede usar una integral para demostrar que esta serie converge. En la figura 7.3_2, dibujamos una secuencia de rectángulos con áreas 1, 1/ 2², 1/ 3², … junto con la función f (x) = 1 / x². Del gráfico vemos que

Por lo tanto, para cada k, la k ésima suma parcial S_k satisface

Concluimos que la secuencia de sumas parciales {S_k} está limitada. También vemos que {{S_k} es una secuencia creciente:

Dado que {S_k} está aumentando y limitado, por el Teorema de convergencia monótona, converge. Por lo tanto, la serie

Converge.

(Figura 7.3_2 La suma de las áreas de los rectángulos es menor que la suma del área del primer rectángulo y el área entre la curva f (x) = 1/x² y el eje x para x ≥ 1. Como el área delimitada por la curva es finita, la suma de las áreas de los rectángulos también es finita.)

Podemos extender esta idea para probar la convergencia o divergencia para muchas series diferentes. Suponga que

es una serie con términos positivos y tal que existe una función continua, positiva y decreciente f donde f (n) = a_n para todos los enteros positivos. Luego, como en la figura 7.3_3 (a), para cualquier número entero k, la suma parcial k cumple S_k

Por lo tanto, si

converge, entonces la secuencia de sumas parciales {S_k} está limitada. Dado que {S_k} es una secuencia creciente, si también es una secuencia acotada, entonces, según el Teorema de convergencia monótona, converge. Concluimos que siconverge, entonces la serie

También converge. Por otro lado, de la figura 7.3_3 (b), para cualquier entero k, la k-ésima suma parcial S_k cumple

(Figura 7.3_3 (a) Si podemos inscribir rectángulos dentro de una región delimitada por una curva y = f (x) y el eje x, y el área delimitada por esas curvas para x ≥ 1 es finita, entonces la suma de las áreas de Los rectángulos también son finita. (b) Si un conjunto de rectángulos circunscribe la región limitada por y = f (x) y el eje x para x ≥ 1 y la región tiene un área infinita, entonces la suma de las áreas de los rectángulos también es infinita.)

TEOREMA 7.3_1. Prueba de la integral

Suponga quees una serie con términos positivos an. Supongamos que existe una función f y un entero positivo N tal que se satisfacen las siguientes tres condiciones: (i)    f es continua, (ii)   f está decreciendo, y (iii)  f (n) = an para todos los enteros n ≥ N. EntoncesAmbas convergen o ambas divergen (ver Figura 7.3_4).

Aunque la convergencia deimplica la convergencia de las series relacionadas, esto no implica que el valor de la integral y la serie sean iguales. Pueden ser diferentes, y a menudo lo son. Por ejemplo,

es una serie geométrica con término inicial a = 1/e y relación r = 1/e, que converge aSin embargo, la integral relacionadasatisface

EJEMPLO ILUSTRATIVO 7.3_2. Usando la Prueba de la Integral

Para cada una de las siguientes series, use la prueba integral para determinar si la serie converge o diverge.

Solución:

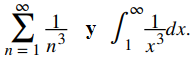
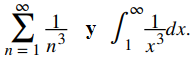
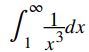
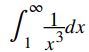
a. CompararNosotros tenemosAsí la integralconverge, y por lo tanto también lo hace la serie

b. CompararYa queLa integraldiverge, y por lo tanto, la seriediverge.