6. Aplicaciones de la integral
6.1. ÁREAS ENTRE CURVAS: Objetivos de aprendizaje
6.1.1. Determinar el área de una región entre dos curvas integrando con respecto a la variable independiente.
6.1.2. Encontrar el área de una región compuesta.
6.1.3. Determinar el área de una región entre dos curvas integrando con respecto a la variable dependiente.
Ejercicios resueltos del Capítulo 6
En Introducción a la integración, desarrollamos el concepto de integral definida para calcular el área debajo de una curva en un intervalo dado. En esta sección, ampliamos esa idea para calcular el área de regiones más complejas. Comenzamos por encontrar el área entre dos curvas que son funciones de x, comenzando con el caso simple en el que el valor de una función siempre es mayor que el otro. Luego observamos casos en los que se cruzan las gráficas de las funciones. Por último, consideramos cómo calcular el área entre dos curvas que son funciones de y.
6.1.1 Área de una región entre dos curvas
Supongamos que f (x) y g(x) sean funciones continuas en un intervalo cerrado [a, b] tal que f (x) ≥ g(x) en [a, b]. Queremos encontrar el área entre las gráficas de las funciones, como se muestra en la siguiente figura.
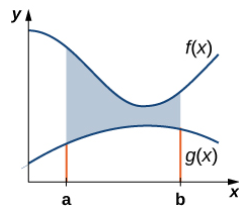
Como lo hicimos antes, vamos a dividir el intervalo en el eje x y aproximar el área entre las gráficas de las funciones con rectángulos. Entonces, para i = 0, 1, 2, …, n, sea P = {xi} una partición regular de [a, b]. Luego, para i = 1, 2, …, n, elija un punto xi* ∈ [xi − 1, xi], y en cada intervalo [xi − 1, xi] construya un rectángulo que se extienda verticalmente desde g (xi*) a f (xi*). La figura 6.2 (a) muestra los rectángulos cuando xi* se selecciona como el punto final izquierdo del intervalo con n = 10. La figura 6.2 (b) muestra un rectángulo representativo en detalle.


La altura de cada rectángulo individual es f (xi*) − g (xi*) y el ancho de cada rectángulo es Δx. Agregando las áreas de todos los rectángulos, vemos que el área entre las curvas se aproxima por
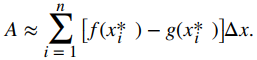
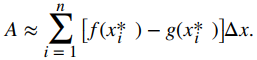
Esta es una suma de Riemann, entonces tomamos el límite cuando n → ∞ y obtenemos


Estos hallazgos se resumen en el siguiente teorema.
Teorema 6.1.1. Encontrar el área entre dos curvas
|
Supongamos que f (x) y g(x) sean funciones continuas tales que f (x) ≥ g(x) en un intervalo [a, b]. Supongamos que R denota la región delimitada arriba por la gráfica de f (x), abajo por la gráfica de g(x), y a la izquierda y derecha por las rectas x = a y x = b, respectivamente. Entonces, el área de R viene dada por
|
Aplicamos este teorema en el siguiente ejemplo.
EJEMPLO ILUSTRATIVO 6.1_1. Hallar el área de una región entre dos curvas
Si R es la región acotada arriba por la gráfica de la función f (x) = x + 4 y abajo por la gráfica de la función g(x) = 3 − x/2 en el intervalo [1, 4], encuentre el área de región R.
Solución:
La región se muestra en la siguiente figura.
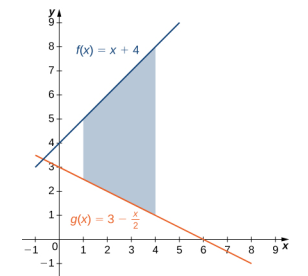

Se tiene que
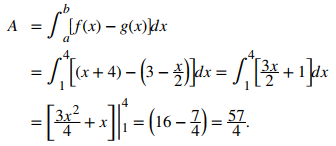
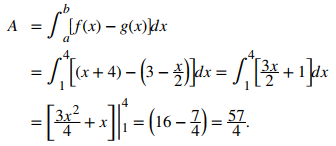
El área de la región es de 57/4 unidades².
Ejercicio de control 6.1_1
Si R es la región limitada por las gráficas de las funciones f (x) = x/2 + 5 y g(x) = x + 1/2 en el intervalo [1, 5], encuentre el área de la región R.
En el ejemplo ilustrativo 6.1_1, definimos el intervalo de interés como parte del enunciado del problema. Sin embargo, con bastante frecuencia queremos definir nuestro intervalo de interés en función de dónde se cruzan las gráficas de las dos funciones. Esto se ilustra en el siguiente ejemplo.
EJEMPLO ILUSTRATIVO 6.1_2. Hallar el área de una región entre dos curvas
Si R es la región limitada arriba por la gráfica de la función f (x) = 9 − (x / 2)² y abajo por la gráfica de la función g(x) = 6 − x, encuentre el área de la región R.
Solución:
La región se muestra en la siguiente figura.
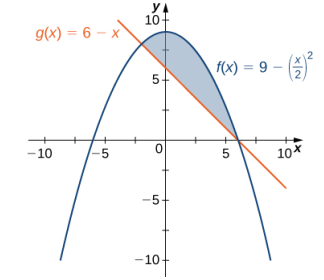

Primero necesitamos calcular dónde se cruzan (intersectan) las gráficas de las funciones. Estableciendo f (x) = g(x), obtenemos
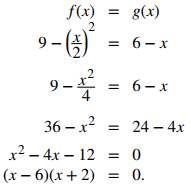
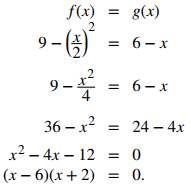
Las gráficas de las funciones se cruzan cuando x = 6 o x = −2, por lo que queremos integrar de −2 a 6. Como f (x) ≥ g(x) para −2 ≤ x ≤ 6, obtenemos
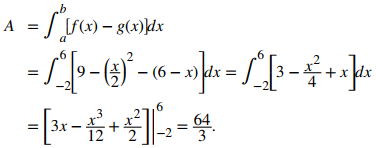
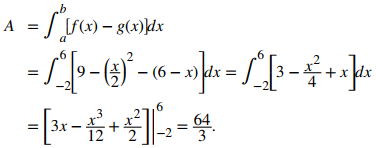
El área de la región es 64/3 unidades².
Ejercicio de control 6.1_2
Si R es la región acotada arriba por la gráfica de la función f (x) = x y abajo por la gráfica de la función g(x) = x⁴, encuentre el área de la región R.
Áreas de regiones compuestas
Hasta ahora, hemos requerido f (x) ≥ g(x) en todo el intervalo de interés, pero ¿qué sucede si queremos ver regiones limitadas por las gráficas de funciones que se cruzan entre sí? En ese caso, modificamos el proceso que acabamos de desarrollar utilizando la función de valor absoluto.
Teorema 6.1.2. Encontrar el área de una región entre curvas que se cruzan
|
Sean f (x) y g(x) funciones continuas en un intervalo cerrado [a, b]. Supongamos que R denota la región entre las gráficas de f (x) y g(x), y que esté delimitada a la izquierda y a la derecha por las rectas x = a y x = b, respectivamente. Entonces, el área de R viene dada por
|
En la práctica, la aplicación del anterior teorema requiere que separemos el intervalo [a, b] y evaluemos varias integrales, dependiendo de cuál de los valores de la función sea mayor en una parte determinada del intervalo. Estudiamos este proceso en el siguiente ejemplo.
EJEMPLO ILUSTRATIVO 6.1_3. Hallar el área de una región delimitada por funciones que se cruzan
Si R es la región entre las gráficas de las funciones f (x) = senx y g(x) = cosx en el intervalo [0, π], encuentre el área de la región R.
Solución:
La región se muestra en la siguiente figura.


Las gráficas de las funciones se intersecan en x = π/4 . Para x∈ [0, π/4], cosx ≥ senx, entonces
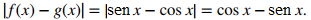
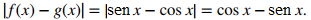
Por otro lado, para x∈ [π/4, π], senx ≥ cosx, entonces
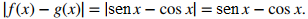
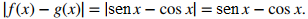
Luego
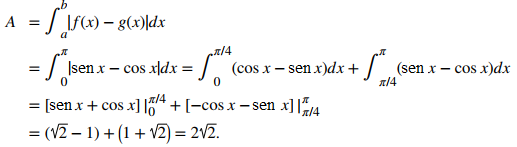
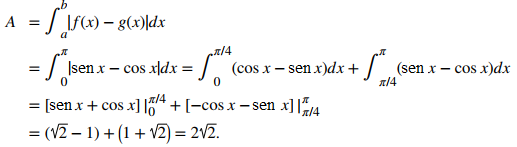
El área de la región es 2√2 unidades².
Ejercicio de control 6.1_3
Si R es la región entre las gráficas de las funciones f (x) = senx y g(x) = cosx en el intervalo [π/2, 2π], encuentre el área de la región R.
EJEMPLO ILUSTRATIVO 6.1_4. Encontrar el área de una región compleja
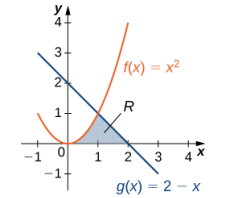
Considere la región que se muestra en la Figura 6.1_6. Encuentre el área de R.


Solución:
Como en el ejemplo 6.1_3, necesitamos dividir el intervalo en dos partes. Las gráficas de las funciones se intersecan en x = 1 (establecer f (x) = g(x) y resolver para x), por lo que evaluamos dos integrales separadas: una sobre el intervalo [0, 1] y otra sobre el intervalo [1 , 2].
En el intervalo [0, 1], la región está acotada arriba por f (x) = x² y abajo por el eje x, así que tenemos
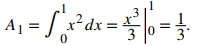
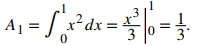
En el intervalo [1, 2], la región está acotada arriba por g(x) = 2 − x y abajo por el eje x, por lo que tenemos
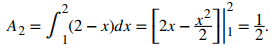
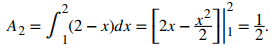
Sumando estas áreas, obtenemos
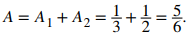
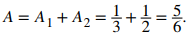
El área de la región es de 5/6 unidades².
Ejercicio de control 6.1_4
Considere la región que se muestra en la siguiente figura. Encuentre el área de R.
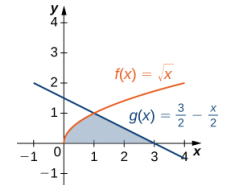
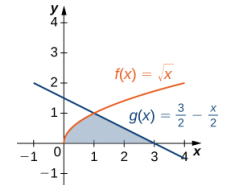
Regiones definidas con respecto a la variable dependiente y
En el ejemplo 6.1_4, tuvimos que evaluar dos integrales separadas para calcular el área de la región. Sin embargo, hay otro enfoque que requiere solo una integral. ¿Qué pasa si tratamos las curvas como funciones de y, en lugar de como funciones de x? Revise la Figura 6.1_6. Tenga en cuenta que la gráfica de la izquierda, que se muestra en rojo, está representada por la función y = f (x) = x². Podríamos fácilmente resolver esto para x y representar la curva mediante la función x = v(y) = √y. (Tenga en cuenta que x = −√y también es una representación válida de la función y = f (x) = x² como función de y. Sin embargo, según la gráfica, está claro que estamos interesados en la raíz cuadrada positiva). De manera similar, la gráfica de la derecha está representada por la función y = g(x) = 2 − x, pero podría representarse fácilmente con la función x = u(y) = 2 − y. Cuando las gráficas se representan como funciones de y, vemos que la región está limitada a la izquierda por la gráfica de una función y a la derecha por la gráfica de la otra función. Por lo tanto, si integramos con respecto a y, necesitamos evaluar solo una integral. Desarrollemos una fórmula para este tipo de integración.
Sean u(y) y v(y) funciones continuas en un intervalo [c, d] tal que u(y) ≥ v(y) para todo y ∈ [c, d]. Queremos encontrar el área entre las gráficas de las funciones, como se muestra en la siguiente figura.
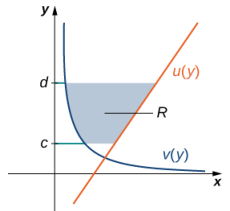

Esta vez, vamos a dividir el intervalo en el eje y y usaremos rectángulos horizontales para aproximar el área entre las funciones. Entonces, para i = 0, 1, 2, …, n, sea Q = {yi} una partición regular de [c, d]. Entonces, para i = 1, 2, …, n, elija un punto y*i ∈ [yi − 1, yi], luego sobre cada intervalo [yi − 1, yi] construya un rectángulo que se extienda horizontalmente desde v(y*i) a u(y*i). La figura 6.1_9 (a) muestra los rectángulos cuando y*i se selecciona como el punto final inferior del intervalo y n = 10. La figura 6.1_9 (b) muestra un rectángulo representativo en detalle.


La altura de cada rectángulo individual es Δy y el ancho de cada rectángulo es u(y*i) − v(y*i). Por lo tanto, el área entre las curvas es aproximadamente
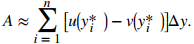
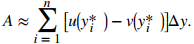
Esta es una suma de Riemann, por lo que tomamos el límite como n → ∞, obteniendo


Estos hallazgos se resumen en el siguiente teorema.
Teorema 6.1.3. Encontrar el área entre dos curvas, integrando a lo largo del eje y.
|
Sean u(y) y v(y) funciones continuas de manera que u(y) ≥ v(y) para todos los y ∈ [c, d]. Supongamos que R denota la región limitada a la derecha por la gráfica de u(y), a la izquierda por la gráfica de v(y), y arriba y abajo por las rectas y = d e y = c, respectivamente. Entonces, el área de R viene dada por
|
EJEMPLO ILUSTRATIVO 6.1_5. Integrar con respecto a y
Repasemos el ejemplo 6.1_4, solo que esta vez integremos con respecto a y. Sea R la región que se muestra en la figura 6.1_9. Encuentre el área de R integrando con respecto a y.

Solución:
Primero debemos expresar las gráficas como funciones de y. Como vimos al comienzo de esta sección, la curva de la izquierda se puede representar con la función x = v(y) = √y, y la curva de la derecha se puede representar con la función x = u(y) = 2 − y.
Ahora tenemos que determinar los límites de la integración. La región está delimitada por debajo por el eje x, por lo que el límite inferior de integración es y = 0. El límite superior de integración está determinado por el punto donde se cruzan las dos gráficas, que es el punto (1, 1), por lo que el límite superior de integración es y = 1. Por tanto, tenemos [c, d] = [0, 1].
Calculando el área de la región, obtenemos
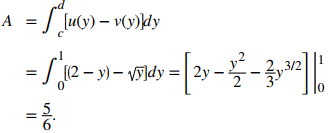
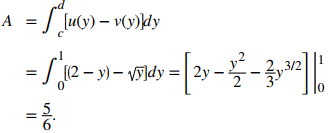
El área de la región es de 5/6 unidades².
Ejercicio de control 6.1_5
Revisemos el ejercicio de control asociado con el ejemplo 6.1_4, solo que esta vez integremos con respecto a y. Sea R la región representada en la siguiente figura. Encuentre el área de R integrando con respecto a y.




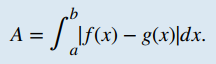

Buenas tardes, quisiera saber donde podría encontrar la resolución del ejercicio 52 de este capítulo 6.1 ya que se me está dificultando. Muchisimas gracias por compartir estos apuntes que me han ayudado mucho.
Excelente todo!!!
Excelente material.
Gracias. Periódicamente publico más apuntes, ejercicios propuestos y ejercicios resueltos sobre temas de cálculo calculo21.com 👀😺
EXCELENTE
Gracias por el comentario. Esta semana publicaré más contenido sobre este tema 😺👀
Profesor excelente el contenido… muy buena la redacción…
Una curiosidad… con que software realiza sus gráficas?
Lo sigo leyendo…
Gracias por compartir sus conocimientos.
Hola Fernando.
Gracias por el comentario e interés. Para llegar a personas como tú es que se realiza este proyecto.
Las gráficas se construyen con el programa Geogebra, complementado con Word, Mathtype, etc. y se organiza todo en Paint. 👀