| 9. Ecuaciones diferenciales | 9.8. La transformada de Laplace |

9.8.3 SOLUCIÓN DE PROBLEMAS DE VALOR INICIAL

Transformadas de Laplace de Derivadas

En el resto de este capítulo, usaremos la transformada de Laplace para resolver problemas de valores iniciales para ecuaciones de segundo orden de coeficientes constantes. Para hacer esto, debemos saber cómo se relaciona la transformada de Laplace de f ′ con la transformada de Laplace de f. El siguiente teorema responde a esta pregunta.

Teorema 9.8.3.1

Supongamos que f es continua en [0, ∞) y de orden exponencial s₀, y f ′ es continua por tramos en [0, ∞). Entonces f  y  f ′ tienen transformadas de Laplace para s > s₀, y

        (9.8.3.1)  ♦

Prueba:

      Sabemos por el Teorema 9.8.1.6 que L(f) está definida para s > s₀. Primero consideramos el caso donde f ′ es continua en [0, ∞). De la integración por partes, se obtiene

        (9.8.3.1)

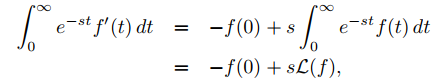
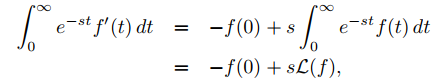
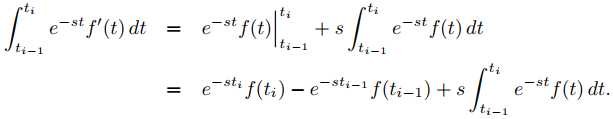
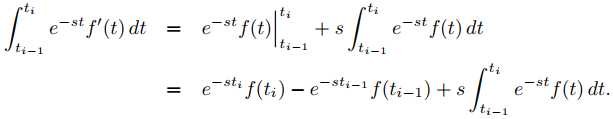
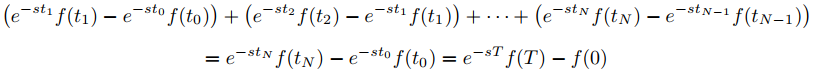
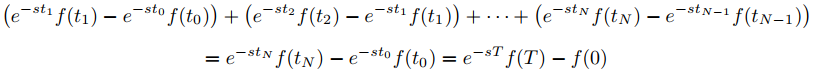
para cualquier T > 0. Como f es de orden exponencial s₀, lim_{T →∞} e^−sT f (T) = 0 y la última integral en (9.8.3.2) converge cuando T → ∞  si  s > s₀. Por lo tantolo que prueba (9.8.3.1). Ahora supongamos que T > 0 y f ′ solo es continua por tramos en [0, T], con discontinuidades en t₁ < t₂ < · · · < t_n−1. Por conveniencia, sea t₀ = 0  y  t_n = T. Integrando por partes se obtieneSumando ambos lados de esta ecuación de i = 1 a n y observando queproduce (9.8.3.2), por lo que (9.8.3.1) sigue como antes.  ♦

Ejemplo 9.8.3.1

En el Ejemplo 9.8.1.4 vimos queAplicando la fórmula del Teorema 9.8.3.1 con f (t) = cosωt se muestra quePor lo tantolo cual concuerda con el resultado correspondiente obtenido en el Ejemplo 9.8.1.4.    ♦

       En la Sección 9.2.1, Ejemplo ilustrativo 9.2.1.3, mostramos que la solución del problema de valor inicial

y′ = ay,  y(0) = y₀,        (9.8.3.3)

es y = y₀e^at. Ahora obtendremos este resultado utilizando la transformada de Laplace.

      Sea Y(s) = L(y) la transformada de Laplace de la solución desconocida de (9.8.3.3). Tomando transformadas de Laplace de ambos lados de (9.8.3.3) se obtiene

L(y′) = L(ay),

que, por el Teorema 9.8.3.1, se puede reescribir como

sL(y) − y(0) = aL(y),

o

sY(s) − y₀ = aY(s).

Resolviendo para Y(s) se obtiene

por lo que

que concuerda con el resultado conocido.

      Necesitamos el siguiente teorema para resolver ecuaciones diferenciales de segundo orden usando la transformada de Laplace.

Teorema 9.8.3.2

Supongamos que f  y  f ′ son continuas en [0, ∞) y de orden exponencial s₀, y que f ″ es continua por tramos en [0, ∞). Entonces f, f ′ y f ″ tienen transformadas de Laplace para s > s₀,

       (9.8.3.4)

y

       (9.8.3.5)  ♦

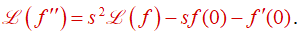
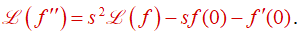
Prueba:

    El Teorema 9.8.3.1 implica que L(f ′) existe y satisface (9.8.3.4) para s > s₀. Para probar que L(f ″) existe y satisface (9.8.3.5) para s >s₀, primero aplicamos el Teorema 9.8.3.1 a g = f ′. Como g satisface las hipótesis del Teorema 9.8.3.1, concluimos que L(g′) está definida y satisface

L(g′) = sL(g) − g(0)

para s > s₀. Sin embargo, dado que g′ = f ′′, esto se puede reescribir como

L(f ′′) = sL(f ′) − f ′(0).

Sustituyendo (9.8.3.4) en esta última ecuación, se obtiene (9.8.3.5). ♦

Resolviendo ecuaciones de segundo orden con la transformada de Laplace

      Ahora usaremos la transformada de Laplace para resolver problemas de valores iniciales para ecuaciones de segundo orden.

Ejemplo 9.8.3.2

Utilice la transformada de Laplace para resolver el problema del valor inicial

       (9.8.3.6)

Solución:

Tomando las transformadas de Laplace de ambos lados de la ecuación diferencial en (9.8.3.6) se obtiene

Lo que reescribimos como

       (9.8.3.7)

Ahora denotamos L(y) = Y(s). El teorema 9.8.3.2 y las condiciones iniciales en (9.8.3.6) implican queySustituyendo las dos últimas ecuaciones en (9.8.3.7) se obtienePor lo tanto

             (9.8.3.8)

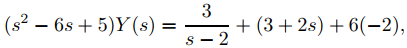
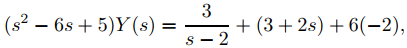
así quey

El método de Heaviside produce la expansión en fracciones parciales

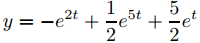
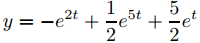
y tomando la transformada inversa de Laplace de cada término en el miembro derecho en la igualdad anterior, se obtienecomo la solución de (9.8.3.6). ♦

      No es necesario escribir todos los pasos que usamos para obtener (9.8.3.8). Para ver cómo evitar esto, apliquemos el método del Ejemplo 9.8.3.2 al problema general de valor inicial

      (9.8.3.9)

      Tomando las transformadas de Laplace de ambos lados de la ecuación diferencial en (9.8.3.9) se obtiene

      (9.8.3.10)

Ahora sea Y(s) = L(y). El Teorema 9.8.3.2 y las condiciones iniciales en (9.8.3.9) implican que

Sustituyendo las transformadas anteriores en (9.8.3.10), se obtiene

      (9.8.3.11)

El coeficiente de Y(s) de la izquierda es el polinomio característico

p(s) = as² + bs + c

de la ecuación complementaria para (9.8.3.9). Usando esto y moviendo los términos que involucran a k₀ y k₁ al lado derecho de (9.8.3.11) se obtiene

        (9.8.3.12)

Esta ecuación corresponde a (9.8.3.8) del Ejemplo 9.8.3.2. Habiendo establecido la forma de esta ecuación en el caso general, es preferible pasar directamente del problema de valor inicial a esta ecuación. Puede que le resulte más fácil de recordar (9.8.3.12) reescrito como

      (9.8.3.13)

Ejemplo 9.8.3.3

Utilice la transformada de Laplace para resolver el problema del valor inicial

      (9.8.3.14)

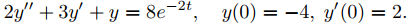
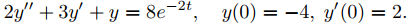
Solución:

El polinomio característico es

y entonces (9.8.3.13) se convierte enResolviendo para Y(s) se obtieneEl método de Heaviside produce la expansión en fracciones parcialesentonces la solución de (9.8.3.14) es

.  ♦

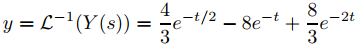
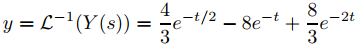
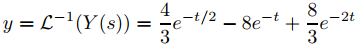
Figura 9.8.3.2: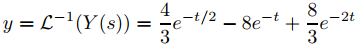   

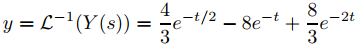
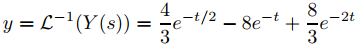
Ejemplo 9.8.3.4

Resolver el problema de valor inicial

      (9.8.3.15)

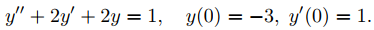
Solución:

El polinomio característico es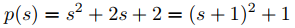

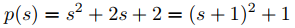
yentonces (9.8.3.13) se convierte en

Resolviendo para Y(s) se obtiene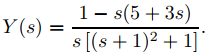

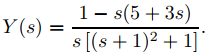
En el ejemplo 9.8.2.8 encontramos que la transformada inversa de esta función es

(Figura 9.8.3.2), que es por tanto la solución del PVI 9.8.3.15. ♦

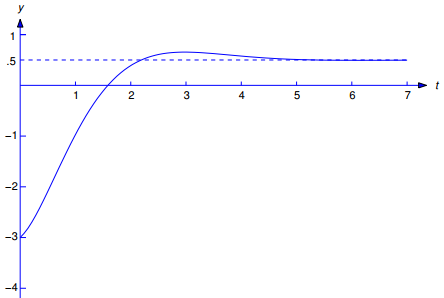
Figura 9.8.3.2: 

OBSERVACIÓN: En nuestros ejemplos aplicamos los Teoremas 9.8.3.1 y 9.8.3.2 sin verificar que la función desconocida y satisface sus hipótesis. Esto es característico de la forma de manipulación formal en la que se utiliza la transformada de Laplace para resolver ecuaciones diferenciales. Cualquier duda sobre la validez del método para resolver una ecuación dada se puede resolver verificando que la función resultante y es la solución del problema dado.