| 3. La derivada |

3.1. DEFINICIÓN DE DERIVADA

Objetivos de aprendizaje:

3.1.1. Reconocer el significado de la tangente a una curva en un punto.
3.1.2. Calcular la pendiente de una recta tangente.
3.1.3. Identificar la derivada como el límite de un cociente de diferenciales.
3.1.4. Calcular la derivada de una función dada en un punto.
3.1.5. Describir la velocidad como una razón de cambio.
3.1.6. Explicar la diferencia entre la velocidad promedio y la velocidad instantánea.
3.1.7. Estimar la derivada a partir de una tabla de valores.

Ahora que tenemos tanto una comprensión conceptual de límite como la capacidad práctica de calcular límites, hemos establecido las bases para nuestro estudio del cálculo, la rama de las matemáticas en la que calculamos derivadas e integrales. La mayoría de los matemáticos e historiadores están de acuerdo en que el cálculo fue desarrollado independientemente por el inglés Isaac Newton (1643–1727) y el alemán Gottfried Leibniz (1646–1716), cuyas imágenes aparecen en la Figura 3.1_1. Cuando atribuimos a Newton y Leibniz el desarrollo del cálculo, nos estamos refiriendo realmente al hecho de que Newton y Leibniz fueron los primeros en comprender la relación entre la derivada y la integral. Ambos matemáticos se beneficiaron del trabajo de predecesores, como Barrow, Fermat y Cavalieri. La relación inicial entre los dos matemáticos parece haber sido amigable; sin embargo, en años posteriores estalló una amarga controversia sobre quién tuvo prioridad en el desarrollo de las ideas que originaron el cálculo. Aunque parece probable que Newton llegó primero a las ideas detrás del cálculo, estamos en deuda con Leibniz por la notación que comúnmente usamos hoy en día.

Rectas Tangentes

Comenzamos nuestro estudio del cálculo revisando la noción de rectas secantes y rectas tangentes. Recuerde que usamos la pendiente de una recta secante a una función en un punto (a, f (a)) para estimar la tasa de cambio, o la razón a la que cambia una variable en relación con otra variable. Podemos obtener la pendiente de la secante eligiendo un valor de x cerca de a y dibujando una recta a través de los puntos (a, f (a)) y (x, f (x)), como se muestra en la Figura 3.1_2. La pendiente de esta rectas viene dada por una ecuación en forma de cociente de diferencias:

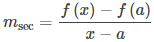
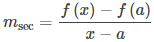
También podemos calcular la pendiente de una recta secante a una función en un valor a usando esta ecuación y reemplazando x con a + h, donde h es un valor cercano a 0. Luego podemos calcular la pendiente de la recta a través de los puntos (a, f (a)) y (a + h, f (a + h)). En este caso, encontramos que la recta secante tiene una pendiente dada por el siguiente cociente de diferencias con incremento h:

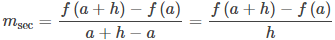
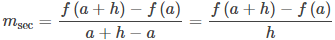
Definición 3.1.1. Cociente de diferencias

Sea f una función definida en un intervalo I que contiene a a. Si x ≠ a está en I, entonces

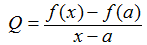
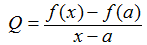
Es un cociente de diferencias.

Además, si se elige h ≠ 0 de modo que a + h esté en I, entonces

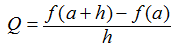
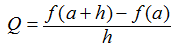
es un cociente de diferencias con incremento h. ◆

Estas dos expresiones para calcular la pendiente de una recta secante se ilustran en la Figura 3.1_2. Veremos que cada uno de estos dos métodos para encontrar la pendiente de una recta secante es valioso. Dependiendo de la configuración, podemos elegir uno u otro. La consideración principal en nuestra elección generalmente depende de la facilidad de cálculo.

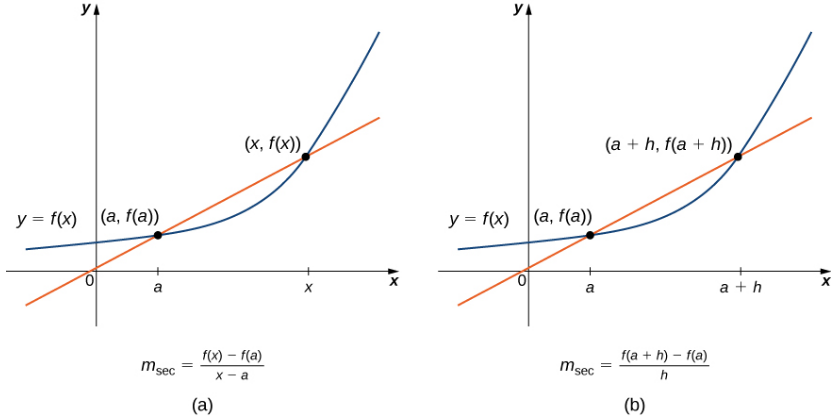
En la figura 3.1_3 (a) vemos que, a medida que los valores de x se acercan a a, las pendientes de las rectas secantes proporcionan mejores estimaciones de la tasa de cambio de la función en a. Además, las rectas secantes se aproximan a la recta tangente de la función en a, que representa el límite de las rectas secantes. De manera similar, la Figura 3.1_3 (b) muestra que a medida que los valores de h se acercan a 0, las rectas secantes también se acercan a la recta tangente. La pendiente de la recta tangente en a es la tasa o razón de cambio de la función en a, como se muestra en la Figura 3.1_3 (c).

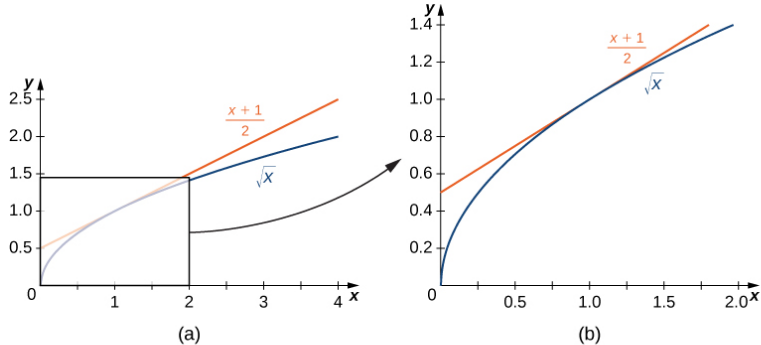
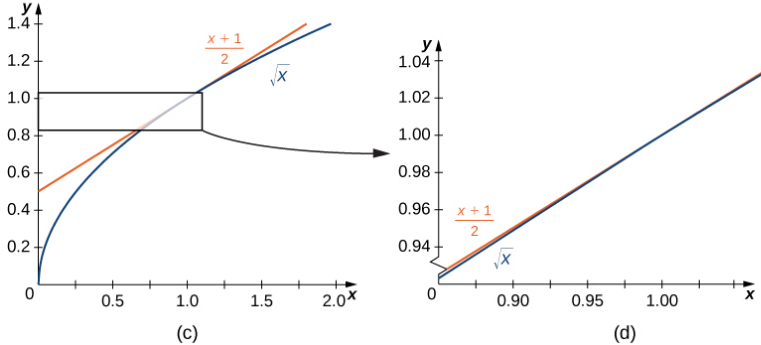
En la Figura 3.1_4 mostramos la gráfica de f (x) = √x y su recta tangente en (1, 1) en una serie de intervalos más ajustados sobre x = 1. A medida que los intervalos se vuelven más estrechos, la gráfica de la función y su recta tangente parecen coincidir, lo que hace que los valores en la recta tangente sean una buena aproximación a los valores de la función para las elecciones de x cercanas a 1. De hecho, la gráfica de f (x) en sí parece ser localmente lineal en la vecindad inmediata de x = 1.

Formalmente podemos definir la recta tangente a la gráfica de una función de la siguiente manera.

Definición 3.1.2. Recta tangente a la gráfica de una función en un punto

Sea f (x) una función definida en un intervalo abierto que contiene a. La recta tangente a f (x) en a es la recta que pasa por el punto (a, f (a)) que tiene pendiente

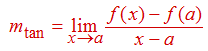
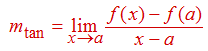
siempre que este límite exista.

De manera equivalente, podemos definir la recta tangente a f (x) en a para que sea la recta que pasa por el punto (a, f (a)) que tiene pendiente

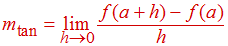
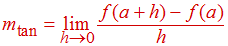
siempre que este límite exista. ♦

Así como hemos usado dos expresiones diferentes para definir la pendiente de una recta secante, usamos dos formas diferentes para definir la pendiente de la recta tangente. En este texto usamos ambas formas de la definición. Como antes, la elección de la definición dependerá de la configuración. Ahora que hemos definido formalmente una recta tangente a una función en un punto, podemos usar esta definición para encontrar ecuaciones de rectas tangentes.

EJEMPLO ILUSTRATIVO 3.1_1. Hallar una recta tangente

Encuentre la ecuación de la recta tangente a la gráfica de f (x) = x² en x = 3.

Solución:
Primero encuentre la pendiente de la recta tangente. En este ejemplo, use la primera ecuación de la definición 3.1.2:

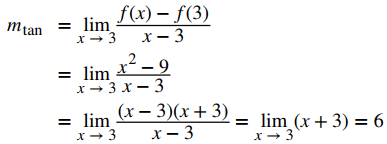
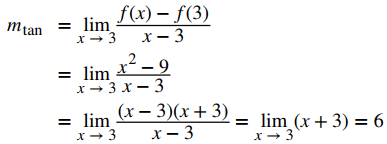
Luego, encuentre un punto en la recta tangente. Como la recta es tangente a la gráfica de f (x) en x = 3, pasa por el punto (3, f (3)). Tenemos que f (3) = 9, entonces la recta tangente pasa por el punto (3, 9).
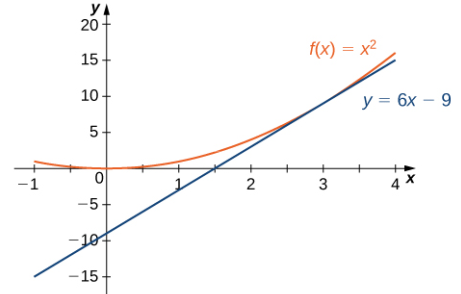
Usando la ecuación punto-pendiente de la recta con la pendiente m = 6 y el punto (3, 9), obtenemos la ecuación de la recta y − 9 = 6 (x − 3). Simplificando, obtenemos y = 6x − 9. La gráfica de f (x) = x² y su recta tangente en 3 se muestran en la Figura 3.1_5.

EJEMPLO ILUSTRATIVO 3.1_2. La pendiente de una recta tangente

Use la segunda ecuación en la definición 3.1.2 para encontrar la pendiente de la recta tangente a la gráfica de f (x) = x² en x = 3.

Solución:
Los pasos son muy similares al ejemplo 3.1_1. Ver la segunda ecuación de la definición 3.1.2.

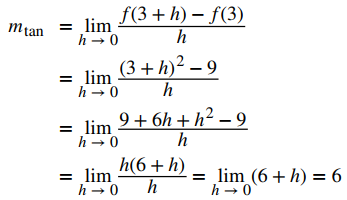
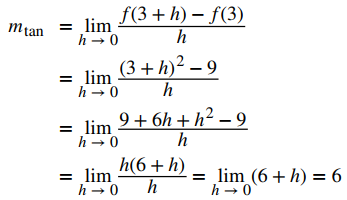
Por su puesto, obtuvimos el mismo valor para la pendiente de la recta tangente usando esta otra ecuación en la definición, demostrando que las fórmulas pueden intercambiarse. ◊

EJEMPLO ILUSTRATIVO 3.1_3. Encontrar la ecuación de una recta tangente

Encuentre la ecuación de la recta tangente a la gráfica de f (x) = 1/x en x = 2.

Solución:
Para hallar la pendiente podemos usar la primera ecuación en la definición 3.1.2, pero como hemos visto, los resultados son los mismos si usamos la la segunda ecuación:

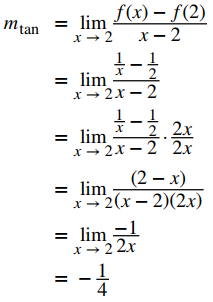
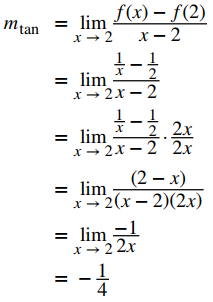
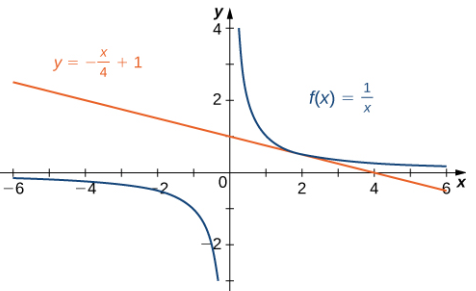
Ahora sabemos que la pendiente de la recta tangente es −1/4. Para hallar la ecuación de la recta tangente, también necesitamos un punto en la recta. Sabemos que f (2) = 1/2. Como la recta tangente pasa a través del punto (2, 1/2), podemos usar la ecuación punto-pendiente de una recta para encontrar la ecuación de la recta tangente. Por lo tanto, la recta tangente tiene la ecuación y = −(1/4)x + 1. Las gráficas de f (x) = 1/x  e  y = −(1/4)x + 1 se muestran en la Figura 3.1_6.

Ejercicio de control 3.1_1

Encuentre la pendiente de la recta tangente a la gráfica de f (x) = √x en x = 4.

La derivada de una función en un punto

El tipo de límite que calculamos para encontrar la pendiente de la recta tangente a una función en un punto ocurre en infinidad de aplicaciones en muchas disciplinas. Estas aplicaciones incluyen velocidad y aceleración en física, funciones de ganancias marginales en negocios y tasas de crecimiento en biología. Este límite ocurre con tanta frecuencia que le damos a este valor un nombre especial: la derivada. El proceso de encontrar una derivada de una función se llama diferenciación.

Definición 3.1.3. Derivada de una función en un punto

Sea f (x) una función definida en un intervalo abierto que contiene a a. La derivada de la función f (x) en a, denotada por f ′(a), se define por

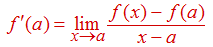
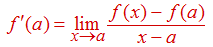
siempre que este límite exista.

Alternativamente, también podemos definir la derivada de f (x) en a como

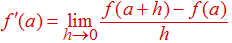
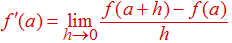
siempre que este límite exista.♦

EJEMPLO ILUSTRATIVO 3.1_4. Estimación de la derivada de una función en un punto

Para f (x) = x², use una tabla de valores para estimar f ′(3) usando la primera ecuación en la definición 3.1.3.

Solución:
Se crea una tabla de valores usando valores de x menores y cercanos a 3 y además valores mayores y cercanos a 3 y luego se evalúan los valores correspondientes de (x² – 9)/(x – 3):

x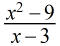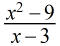
2.9	5.9
2.99	5.99
2.999	5.999
3.001	6.001
3.01	6.01
3.1	6.1

Después de examinar la tabla, vemos que una buena estimación es f ′ (3) = 6.

Ejercicio de control 3.1_2

Para f (x) = x², use una tabla para estimar f ′(3) usando la ecuación lim_x→h ( f (x + h) − f (h))/h.

EJEMPLO ILUSTRATIVO 3.1_5. Calculando la derivada de una función en un punto

Para f (x) = 3x² − 4x + 1, calcule f ′(2) usando la primera ecuación en la definición 3.1.3

Solución:
Sustituya la función y el valor dado directamente en la ecuación.

Aplique la fórmula de la definición

Sustituya f (x) = 3x² – 4x + 1  y  f (2) = 5

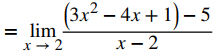
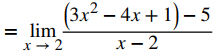
Simplifica y factoriza el numerador

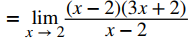
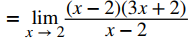
Cancele el factor común

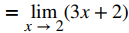
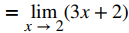
Evalúe el límite

◊

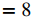
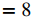
EJEMPLO ILUSTRATIVO 3.1_6. Revisando la Derivada

Para f (x) = 3x² − 4x + 1, encuentre f ′(2) usando la segunda ecuación dada en la definición 3.1.3.

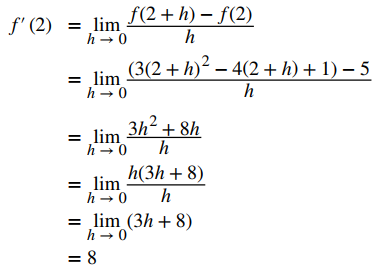
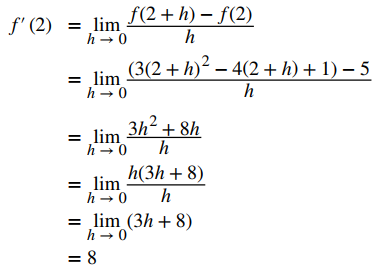
Los resultados son los mismos si usamos la primera o la segunda ecuación dadas en la definición 3.1.3 ◊

Ejercicio de control 3.1_3

Para f (x) = x² + 3x + 2, encuentre f ′(1).

Velocidades y tasas de cambio

Ahora que sabemos evaluar una derivada, podemos usarla en aplicaciones de velocidad.

Tenga presente que si s(t) es la posición de un objeto que se mueve a lo largo de un eje de coordenadas, la velocidad media del objeto durante un intervalo de tiempo [a, t] si t > a o [t, a] si t < a está dada por el cociente de diferencias

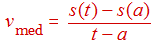
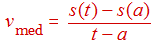
A medida que los valores de t se acercan a a, los valores de la velocidad media, v_med, se aproximan al valor que llamamos velocidad instantánea en a. Es decir, la velocidad instantánea en a, denotada por v (a), viene dada por

Para comprender mejor la relación entre la velocidad media y la velocidad instantánea, vea la Figura 3.1_7. En esta figura, la pendiente de la recta tangente (que se muestra en naranja) es la velocidad instantánea del objeto en el tiempo t = a cuya posición en el tiempo t viene dada por la función s(t). La pendiente de la recta secante (que se muestra en verde) es la velocidad media del objeto durante el intervalo de tiempo [a, t].

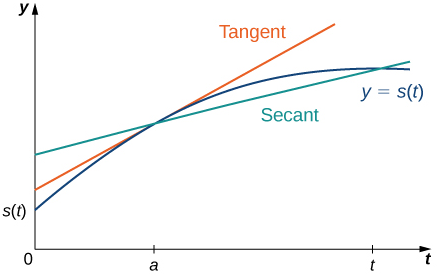
Podemos usar la primera ecuación dada en la definición 3.1.3 para calcular la velocidad instantánea, o podemos estimar la velocidad de un objeto en movimiento usando una tabla de valores. Luego podemos confirmar la estimación utilizando la ecuación dada para la velocidad media .

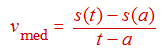
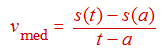
EJEMPLO ILUSTRATIVO 3.1_7. Valor estimado de la velocidad

Un peso de plomo en un resorte oscila hacia arriba y hacia abajo. Su posición en el tiempo t con respecto a una recta horizontal fija está dada por s(t) = sent (Figura 3.1_8). Use una tabla de valores para estimar v(0). Verifique la estimación utilizando la primera ecuación dada en la Definición 3.1.3.

Solución:
Podemos estimar la velocidad instantánea en t = 0 calculando una tabla de velocidades promedio usando valores de t cercanos a 0, como se muestra en la siguiente tabla:

t
-0.1	0.998334166
-0.01	0.9999833333
-0.001	0.999999833
0.001	0.999999833
0.01	0.9999833333
0.1	0.998334166

De la tabla vemos que la velocidad promedio durante el intervalo de tiempo [−0.1, 0] es 0.998334166, la velocidad promedio durante el intervalo de tiempo [−0.01, 0] es 0.9999833333, y así sucesivamente. Usando esta tabla de valores, parece que una buena estimación es v(0) = 1.
Al usar la primera ecuación dada en la definición 3.1.3, podemos ver que

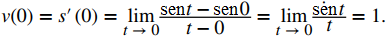
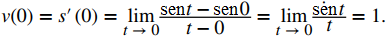
Por lo tanto, de hecho, v(0) = 1. ◊

Ejercicio de control 3.1_4

Se deja caer una roca desde una altura de 64 pies. Su altura sobre el suelo en el tiempo t segundos después viene dada por s(t) = −16t² + 64, 0 ≤ t ≤ 2. Encuentre la velocidad instantánea de la roca 1 segundo después de ser soltada.

       Como hemos visto a lo largo de esta sección, la pendiente de una recta tangente a una función y la velocidad instantánea son conceptos relacionados. Cada uno se halla calculando una derivada y cada uno mide la tasa de cambio instantánea de una función, o la tasa de cambio de una función en cualquier punto de la función.

Definición 3.1.4. Tasa de cambio instantáneo

La tasa o razón de cambio instantáneo de una función f (x) en un valor a es su derivada f ′(a).

 

EJEMPLO ILUSTRATIVO 3.1_8. Estimación de la tasa de cambio de la velocidad

Alcanzando una velocidad máxima de 270.49 mph, el Hennessey Venom GT es uno de los autos más rápidos del mundo. En las pruebas pasó de 0 a 60 mph en 3.05 segundos, de 0 a 100 mph en 5.88 segundos, de 0 a 200 mph en 14.51 segundos, y de 0 a 229.9 mph en 19.96 segundos. Use estos datos para sacar una conclusión sobre la tasa de cambio de la velocidad (es decir, su aceleración) a medida que se acerca a 229.9 mph. ¿La razón a la que el automóvil está acelerando parece aumentar, disminuir o ser constante?

Solución:
Primero observe que 60 mph = 88 pies/s, 100 mph ≈146.67 pies/s, 200 mph ≈293.33 pies/s, y 229.9 mph 7337.19 pies/s. Podemos resumir la información en una tabla.

t	v(t)
0	0
3.05	88
5.88	147.67
14.51	293.33
19.96	337.19

Ahora calcule la aceleración promedio del automóvil en pies por segundo por segundo en intervalos de la forma [t, 19.96] a medida que t se aproxima a 19.96, como se muestra en la siguiente tabla.

t	[v(t) − v(19.96)]/[t −19.96] = [v(t) − 337.19]/[t − 19.96]
0.0	16.89
3.05	14.74
5.88	13.46
14.51	8.05

La razón a la que el automóvil está acelerando disminuye a medida que su velocidad se acerca a 229.9 mph (337.19 pies / s). ◊

EJEMPLO ILUSTRATIVO 3.1_9. Tasa de cambio de la temperatura

Un propietario establece el termostato para que la temperatura en la casa comience a bajar de 70° F a las 9 p.m., alcance un mínimo de 60° durante la noche y vuelva a subir a 70° a las 7 a.m. de la mañana siguiente. Suponga que la temperatura en la casa está dada por T(t) = 0.4t² − 4t + 70 para 0 ≤ t ≤ 10, donde t es el número de horas después de las 9 p.m. Encuentre la tasa de cambio instantánea de la temperatura a medianoche.

Solución:
Dado que la medianoche son 3 horas después de las 9 p.m., queremos calcular T ′(3).

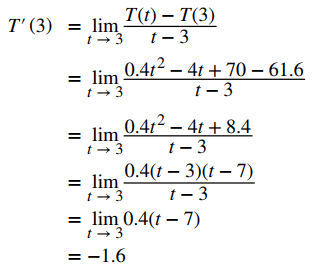
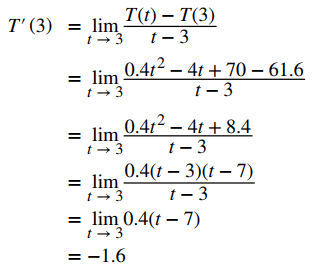
La tasa de cambio instantánea de la temperatura a medianoche es de −1,6°F por hora. ◊

EJEMPLO ILUSTRATIVO 3.1_10. Tasa de cambio de una ganancia

Una empresa de juguetes puede vender x juegos electrónicos a un precio de p = −0.01x + 400 dólares por juego. El costo de fabricación de x juegos viene dado por C(x) = 100x + 10,000 dólares. Encuentre la tasa de cambio de la ganancia cuando se producen 10,000 juegos. ¿Debería la empresa de juguetes aumentar o disminuir la producción?

Solución:
El beneficio P(x) obtenido al producir x juegos está dado por R(x) − C(x), donde R(x) es el ingreso obtenido de la venta de x juegos. Como la compañía puede vender x juegos a p = −0.01x + 400 por juego,

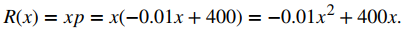
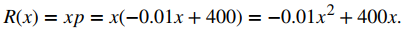
Por consiguiente,

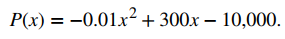
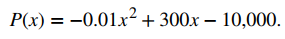
Por lo tanto, al evaluar la tasa de cambio de la ganancia se obtiene

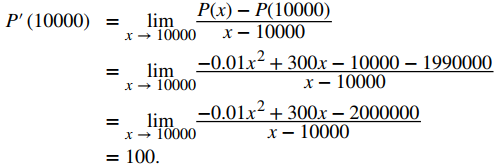
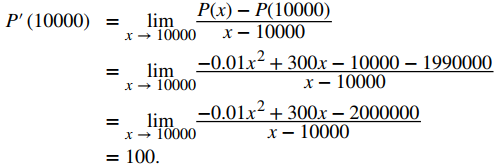
Dado que la tasa de cambio de la ganancia P ′(10,000) > 0 y P(10,000) > 0, la compañía debe aumentar la producción. ◊

Ejercicio de control 3.1_5

Una cafetería determina que la ganancia diaria de bollos que se obtiene al cobrar s dólares por bollo es P(s) = −20s² + 150s − 10. La cafetería cobra actualmente $ 3.25 por bollo. Encuentre P′(3.25), la tasa de cambio de la ganancia cuando el precio es $ 3.25 y decida si la cafetería debería considerar subir o bajar los precios de los bollos.