| 9. Ecuaciones diferenciales | 9.12. Soluciones de Fourier de ecuaciones diferenciales parciales |

9.12.3  La ecuación de Laplace en coordenadas rectangulares

La temperatura u = u(x, y, t) en una placa bidimensional satisface la ecuación de calor bidimensional

u_t = a²(u_xx + u_yy),        (9.12.3.1)

donde (x, y) varía en el interior de la placa y t > 0. Para encontrar una solución de (9.12.3.1), es necesario especificar la temperatura inicial u(x, y, 0) y las condiciones de frontera que deben cumplirse. Sin embargo, a medida que t → ∞, la influencia de la condición inicial decae, por lo que

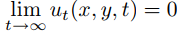
y la temperatura se aproxima a una distribución de estado estacionario u = u(x, y) que satisface

u_xx + u_yy = 0.        (9.12.3.2)

Esta es la ecuación de Laplace. Esta ecuación también surge en aplicaciones a la mecánica de fluidos y la teoría del potencial; de hecho, también se le llama ecuación de potencial. Buscamos soluciones de (9.12.3.2) en una región R que satisfagan condiciones específicas, llamadas condiciones de frontera, en la frontera de R. Por ejemplo, podemos exigir que u asuma valores prescritos en la frontera. Esto se llama condición de Dirichlet, y el problema se llama problema de Dirichlet. O podemos requerir que la derivada normal de u en cada punto (x, y) en la frontera asuma los valores prescritos. Esto se llama condición de Neumann, y el problema se llama problema de Neumann. En algunos problemas imponemos condiciones de Dirichlet sobre una parte de la frontera y condiciones de Neumann sobre el resto. Entonces decimos que las condiciones de contorno y el problema son mixtos.

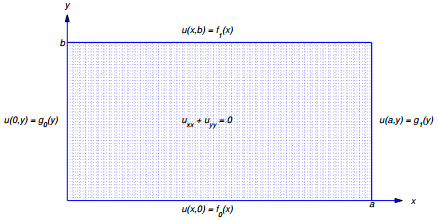
      Resolver problemas de valores en la frontera para (9.12.3.2) sobre regiones generales está más allá del alcance de este libro, por lo que consideramos solo regiones muy simples. Comenzamos considerando la región rectangular que se muestra en la figura 9.12.3.1.

Figura 9.12.3.1 Una región rectangular y su contorno (frontera)

      Las posibles condiciones de contorno para esta región se pueden escribir como

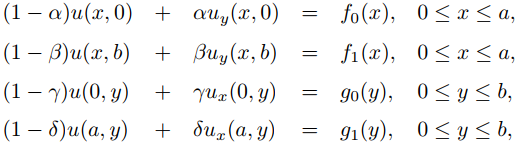
donde α, β, γ y δ pueden ser 0 o 1; por lo tanto, hay 16 posibilidades. Sea PVF(α, β, γ, δ)(f₀, f₁, g₀, g₁) el problema de encontrar una solución de (9.12.3.2) que satisfaga estas condiciones. Este es un problema de Dirichlet si

α = β = γ = δ = 0

(Figura 9.12.3.2), o un problema de Neumann si

α = β = γ = δ = 1

(Figura 9.12.3.3). Los otros 14 problemas son mixtos.

Figura 9.12.3.2 Un problema de Dirichlet

Figura 9.12.3.3 Un problema de Neumann

      Dado (α, β, γ, δ), la suma de las soluciones de

PVF(α, β, γ, δ)(f₀, 0, 0, 0),    PVF(α, β, γ, δ)(0, f₁, 0, 0),

PVF(α, β, γ, δ)(0, 0, g₀, 0)     y    PVF(α, β, γ, δ)(0, 0, 0, g₁)

es una solución de

PVF(α, β, γ, δ)(f₀, f₁, g₀, g₁).

Por lo tanto, nos concentramos en problemas donde solo una de las funciones f₀, f₁, g₀, g₁ no es idénticamente cero. Hay 64 (¡cuéntalos!) problemas de esta forma. Cada uno tiene condiciones de contorno homogéneas en tres lados del rectángulo y una condición de contorno no homogénea en el cuarto. Usamos la separación de variables para encontrar infinitas funciones que satisfagan la ecuación de Laplace y las tres condiciones de frontera homogéneas en el rectángulo abierto. Luego usamos estas soluciones como bloques de construcción para construir una solución formal de la ecuación de Laplace que también satisfaga la condición de frontera no homogénea. Dado que no es factible considerar los 64 casos, restringiremos nuestra atención en el texto a solo cuatro. Otros se discuten en los ejercicios.

      Si v(x, y) = X(x)Y(y) entonces

v_xx + v_yy = X′′Y + XY′′ = 0

para todo (x, y) si y solo si

o todos (x, y), donde k es una constante de separación. Esta ecuación es equivalente a

X′′ − kX = 0,   Y′′ + kY = 0.        (9.12.3.3)

A partir de aquí, la estrategia depende de las condiciones de contorno. Ilustramos esto con ejemplos.

Ejemplo ilustrativo 9.12.3.1

Defina la solución formal de

       (9.12.3.4)

(Figura 9.12.3.4).

Figura 9.12.3.4 El problema del valor en la frontera (9.12.3.4)

Solución:

Las condiciones de frontera en (9.12.3.4) requieren productos v(x, y) = X(x)Y(y) tales que X(0) = X(a) = Y(b) = 0; por tanto, hacemos k = −λ en X′′ − kX = 0,   Y′′ + kY = 0 (9.12.3.3). Por lo tanto, X e Y deben satisfacer

X′′ + λX = 0,   X(0) = 0,   X(a) = 0        (9.12.3.5)

y

Y′′ − λY = 0,   Y(b) = 0.        (9.12.3.6)

Del Teorema 9.11.1.2, los valores propios de (9.12.3.5) son λ_n = n²π²/a², con funciones propias asociadas

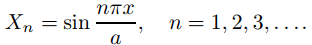
Sustituyendo λ = n²π²/a² en (9.12.3.6) se obtiene

Y′′ − (n²π²/a²)Y = 0,   Y(b) = 0,

para que podamos tomar

      (9.12.3.7)

sin embargo, debido a la condición de Dirichlet no homogénea en y = 0, es mejor exigir que Y_n(0) = 1, lo que se puede lograr dividiendo el lado derecho de (9.12.3.7) por su valor en y = 0; así, tomamos

Entonces

satisface (9.12.3.4) con

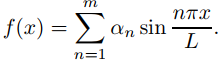
Por lo tanto, si f es una función suave por partes arbitraria en [0, a], definimos la solución formal de (9.12.3.4) como

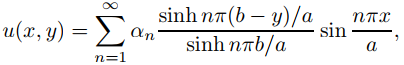        (9.12.3.8)

donde

es la serie de senos de Fourier de f en [0, a]; es decir,

    ♦

Si y < b entonces

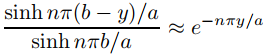      (9.12.3.9)

para n grande, entonces la serie en (9.12.3.8) converge si 0 < y < b; además, ya que también

para n grande, el Teorema 9.12.1.1 aplicado dos veces con z = x y dos veces con z = t, muestra que u_xx y u_yy pueden obtenerse derivando u término por término si 0 < y < b. (Ejercicio 37). Por tanto, u satisface la ecuación de Laplace en el interior del rectángulo de la Figura 9.12.3.4. Además, la serie en (9.12.3.8) también converge en la frontera del rectángulo y satisface las tres condiciones de frontera homogéneas en (9.12.3.4). Por lo tanto, dado que u(x, 0) = S(x) para 0 ≤ x ≤ L, u es una solución real de (9.12.3.5) si y solo si S(x) = f (x) para 0 ≤ x ≤ a. Del Teorema 9.11.3.2, esto es cierto si f es continua y suave por partes en [0, L], y f (0) = f (L) = 0.

Ejemplo ilustrativo 9.12.3.2

Resuelve (9.12.3.4) con f (x) = x(x² − 3ax + 2a²).

Solución:

Del Ejemplo 9.11.3.6,

Por lo tanto

      (9.12.3.10)

      Para calcular valores aproximados de u(x, y), debemos usar sumas parciales de la forma

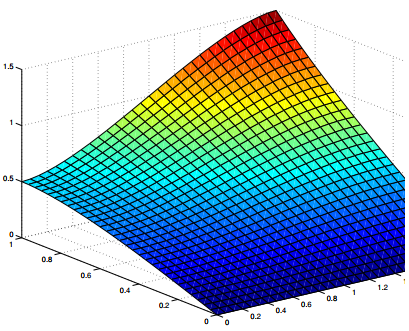
Debido a (9.12.3.9), los valores pequeños de m brindan suficiente precisión para la mayoría de las aplicaciones si 0 < y < b. Además, el factor n³ en el denominador en (9.12.3.10) asegura que esto también sea cierto para y = 0. Para fines gráficos, elegimos a = 2, b = 1 y m = 10. La Figura 9.12.3.5 muestra la superficie

u = u(x, y),   0 ≤ x ≤ 2,   0 ≤ y ≤ 1,

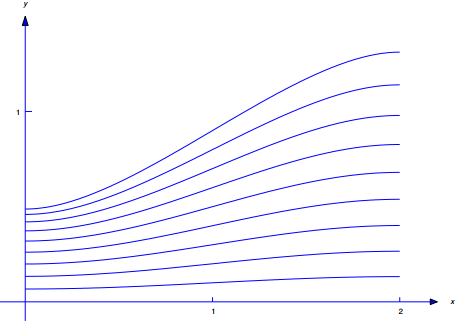
mientras que la Figura 9.12.3.6 muestra las curvas

u = u(x, 0.1k),   0 ≤ x ≤ 2,   k = 0, 1, . . ., 10.    ♦

Figura 9.12.3.5

Figura 9.12.3.6

Ejemplo ilustrativo 9.12.3.3

Defina la solución formal de

      (9.12.3.11)

(Figura 9.12.3.7).

Figura 9.12.3.7 El problema de valor en la frontera (9.12.3.11)

Solución:

Las condiciones de frontera en (9.12.3.11) requieren productos v(x, y) = X(x)Y(y) tales que X′(0) = X′(a) = Y(0) = 0; por lo que hacemos k = −λ en  X′′ − kX = 0, Y′′ + kY = 0 (9.12.3.3). Por lo tanto, X e Y deben satisfacer

X′′ + λX = 0,   X′(0) = 0,   X′(a) = 0        (9.12.3.12)

y

Y′′ − λY = 0,   Y(0) = 0.        (9.12.3.13)

Del Teorema 9.11.1.3, los valores propios de (9.12.3.12) son λ = 0, con la función propia asociada X₀ = 1, y λ_n = n²π²/a², con las funciones propias asociadas

Como Y₀ = y satisface (9.12.3.13) con λ = 0, tomamos v₀(x, y) = X₀(x)Y₀(y) = y. Sustituyendo λ = n²π²/a² en (9.12.3.13) se obtiene

Y′′ − (n²π²/a²)Y = 0,   Y(0) = 0,

para que podamos tomar

      (9.12.3.14)

Sin embargo, debido a la condición de Neumann no homogénea en y = b, es mejor exigir que Y′_n(b) = 1, lo cual se puede lograr dividiendo el lado derecho de (9.12.3.14) por el valor de su derivada en y = b; de este modo,

Entonces

así

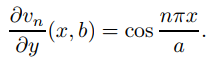
Por tanto, v_n satisface (9.12.3.11) con f (x) = cosnπx/a. Más generalmente, si α₀,  . . . , α_m son constantes arbitrarias entonces

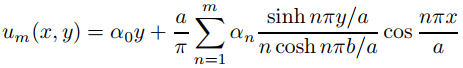
satisface (9.12.3.11) con

Por lo tanto, si f es una función suave por partes arbitraria en [0, a], definimos la solución formal de (9.12.3.11) como

donde

es la serie de coseno de Fourier de f en [0, a]; es decir,

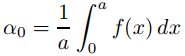    y        ♦

Ejemplo ilustrativo 9.12.3.4

Resuelva (9.12.3.11) con f (x) = x.

Solución:

Del Ejemplo 9.11.3.1

Por lo tanto

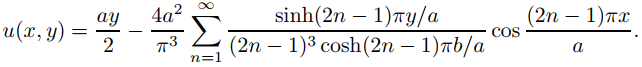        (9.12.3.15)

Para fines gráficos, elegimos a = 2, b = 1, y conservamos los términos hasta n = 10 en (9.12.3.15). La Figura 9.12.3.8 muestra la superficie

u = u(x, y),   0 ≤ x ≤ 2,   0 ≤ y ≤ 1,

mientras que la Figura 9.12.3.9 muestra las curvas

u = u(x, .1k),   0 ≤ x ≤ 2,   k = 0, 1, . . ., 10.    ♦

Figura 9.12.3.8

Figura 9.12.3.9

Ejemplo ilustrativo 9.12.3.5

Defina la solución formal de

      (9.12.3.16)

(Figura 9.12.3.10).

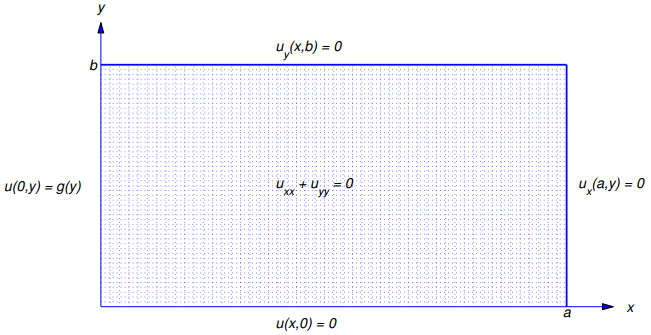
Figura 9.12.3.10 El problema de valor en la frontera (9.12.3.16)

Solución:

Las condiciones de frontera en (9.12.3.16) requieren productos v(x, y) = X(x)Y(y) tales que Y(0) = Y′(b) = X′(a) = 0; por tanto, hacemos k = λ en X′′ − kX = 0,   Y′′ + kY = 0 (9.12.3.3). Por lo tanto, X e Y deben satisfacer

X′′ − λX = 0,   X′(a) = 0        (9.12.3.17)

y

Y′′ + λY = 0,   Y(0) = 0,   Y′(b) = 0.        (9.12.3.18)

Del Teorema 9.11.1.4, los valores propios de (9.12.3.18) son λn = (2n − 1)²π²/4b², con funciones propias asociadas

Sustituyendo λ = (2n − 1)²π²/4b² en (9.12.3.17) se obtiene

X′′ − ((2n − 1)²π²/4b²)X = 0,   X′(a) = 0,

para que podamos tomar

      (9.12.3.19)

Sin embargo, debido a la condición de Dirichlet no homogénea en x = 0, es mejor exigir que X_n(0) = 1, lo que se puede lograr dividiendo el lado derecho de (9.12.3.19) por su valor en x = 0; de este modo,

Entonces

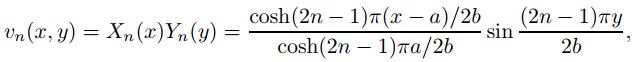
así

Por tanto, v_n satisface (9.12.3.16) con g(y) = sen(2n − 1)πy/2b. Más generalmente, si α₁, . . . , α_m son constantes arbitrarias entonces

satisface (9.12.3.16) con

Por lo tanto, si g es una función suave por partes arbitraria en [0, b], definimos la solución formal de (9.12.3.16) como

donde

es la serie mixta de senos de Fourier de g en [0, b]; es decir,

    ♦

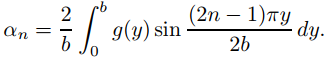Ejemplo ilustrativo 9.12.3.6

Resuelve (9.12.3.16) con g(y) = y(2y² − 9by + 12b²)

Solución:

Del Ejemplo 9.11.3.8,

Por lo tanto

    ♦

Ejemplo ilustrativo 9.12.3.7

Defina la solución formal de

      (9.12.3.20)

(Figura 9.12.3.11).

Figura 9.12.3.11 El problema del valor en la frontera (9.12.3.20)

Solución:

Las condiciones de frontera en (9.12.3.20) requieren productos v(x, y) = X(x)Y(y) tales que Y′(0) = Y(b) = X′(0) = 0; por tanto, hacemos k = λ en (9.12.3.3). Por lo tanto, X e Y deben satisfacer

X′′ − λX = 0,   X′(0) = 0        (9.12.3.21)

y

Y′′ + λY = 0,   Y′(0) = 0,   Y(b) = 0.        (9.12.3.22)

Del Teorema 9.11.1.4, los valores propios de (9.12.3.22) son λ_n = (2n − 1)²π²/4b², con funciones propias asociadas

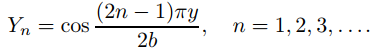
Sustituyendo λ = (2n − 1)²π²/4b² en (9.12.3.21) se obtiene

X′′ − ((2n − 1)²π²/4b²)X = 0,   X′(0) = 0,

para que podamos tomar

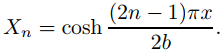      (9.12.3.23)

Sin embargo, debido a la condición de Neumann no homogénea en x = a, es mejor exigir que X′_n(a) = 1, lo que se puede lograr dividiendo el lado derecho de (9.12.3.23) por el valor de su derivada en x = a; de este modo,

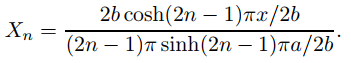
Entonces

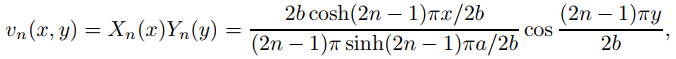
así

Por tanto, v_n satisface (9.12.3.20) con g(y) = cos(2n − 1)πy/2b. Más generalmente, si α₁, . . . , α_m son constantes arbitrarias entonces

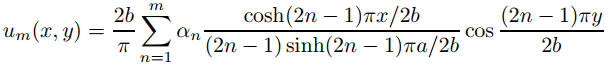
satisface (9.12.3.20) con

Por lo tanto, si g es una función suave por partes arbitraria en [0, b], definimos la solución formal de (9.12.3.20) como

donde

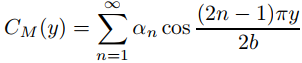
es la serie mixta de cosenos de Fourier de g en [0, b]; es decir,

    ♦

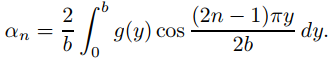Ejemplo ilustrativo 9.12.3.8

esuelva (9.12.3.20) con g(y) = y − b.

Solución:

Del Ejemplo 9.11.3.3,

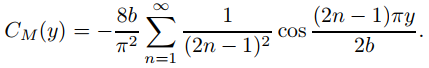
Por lo tanto

    ♦

Ecuación de Laplace para una franja semi-infinita

Ahora buscamos soluciones de la ecuación de Laplace en la franja semi-infinita

S: {0 < x <a,  y > 0}

(Figura 9.12.3.12) que satisfacen condiciones de frontera homogéneas en x = 0  y  x = a, y una condición no homogénea de Dirichlet o Neumann en y = 0. Un ejemplo de tal problema es

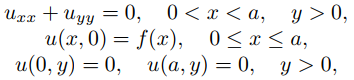      (9.12.3.24)

Figura 9.12.3.12 Un problema de valores en la frontera en una franja semi-infinita

      Las condiciones de contorno en este problema no son suficientes para determinar u, porque si u₀ = u₀(x, y) es una solución y K es una constante entonces

también es una solución. (Compruebe). Sin embargo, si también requerimos, por razones físicas, que la solución permanezca acotada para todo (x, y) en S, entonces K = 0 y esta dificultad se elimina.

Ejemplo ilustrativo 9.12.3.9

Defina la solución formal acotada de (9.12.3.24).

Solución:

Procediendo como en la solución del ejemplo 9.12.3.1, encontramos que las funciones de bloques de construcción son de la forma

donde

Por lo tanto

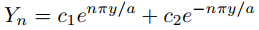
donde c₁ y c₂ son constantes. Aunque las condiciones de frontera en (9.12.3.24) no restringen c₁ y c₂, debemos establecer c₁ = 0 para asegurar que Y_n esté acotado. Dejando c₂ = 1 rendimientos

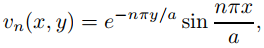
y definimos la solución formal acotada de (9.12.3.24) como

donde

es la serie de senos de Fourier de f en [0, a].    ♦

      Vea los ejercicios 29 a 34 para otros problemas de valores en la frontera en una franja semi-infinita.