| 9. Ecuaciones diferenciales | 9.10. Sistemas lineales de ecuaciones diferenciales |
9.10.3 TEORÍA BÁSICA DE LOS SISTEMAS LINEALES HOMOGÉNEOS
En esta sección consideramos sistemas lineales homogéneos y′ = A(t)y, donde A = A(t) es una función de matriz continua n × n en un intervalo (a, b). La teoría de sistemas lineales homogéneos tiene mucho en común con la teoría de ecuaciones escalares lineales homogéneas, que consideramos en las secciones 9.2.1, 9.5.1 y 9.9.1.
Siempre que nos refiramos a soluciones de y′ = A(t)y nos referiremos a soluciones en (a, b). Como y ≡ 0 es obviamente una solución de y′ = A(t)y, la llamamos solución trivial. Cualquier otra solución es no trivial.
Si y1, y2,. . . , yn son funciones vectoriales definidas en un intervalo (a, b) y c1, c2,. . . , cn son constantes, entonces
y = c1y1 + c2y2 + · · · + cnyn (9.10.3.1)
es una combinación lineal de y1, y2,. . . , yn. Es fácil demostrar que si y1, y2,. . . , yn son soluciones de y′ = A(t)y en (a, b), entonces también lo es cualquier combinación lineal de y1, y2,. . . , yn (ejercicio 1). Decimos que {y1, y2,. . . , yn} es un conjunto fundamental de soluciones de y′ = A(t)y en (a, b) en si la misma solución de y′ = A(t)y en (a, b) se puede escribir como una combinación lineal de y1, y2,. . . , yn, como en (9.10.3.1). En este caso decimos que (9.10.3.1) es la solución general de y′ = A(t)y en (a, b).
Se puede demostrar que si A es continua en (a, b) entonces y′ = A(t)y tiene infinitos conjuntos fundamentales de soluciones en (a, b) (Ejercicios 15 y 16). La siguiente definición ayudará a caracterizar conjuntos fundamentales de soluciones de y′ = A(t)y.
Decimos que un conjunto {y1, y2,. . ., yn} de n funciones vectoriales es linealmente independiente en (a, b) si las únicas constantes c1, c2,. . . , cn tal que
c1y1(t) + c2y2(t) + · · · + cnyn(t) = 0, a < t < b, (9.10.3.2)
son c1 = c2 = · · · = cn = 0. Si (9.10.3.2) se cumple para algún conjunto de constantes c1, c2,. . . , cn que no son todos cero, entonces {y1, y2,. . ., yn} es linealmente dependiente en (a, b).
El siguiente teorema es análogo a los Teoremas 9.5.1.3 y 9.9.1.2
Teorema 9.10.3.1
Suponga que la matriz de n × n A = A(t) es continua en (a, b). Entonces un conjunto {y1, y2,. . ., yn} de n soluciones de y′ = A(t)y en (a, b) es un conjunto fundamental si y solo si es linealmente independiente en (a, b). ♦
Ejemplo ilustrativo 9.10.3.1
Demuestre que los vectores de funciones


son linealmente independientes en cada intervalo (a, b).
Solución:
Suponga que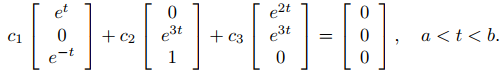
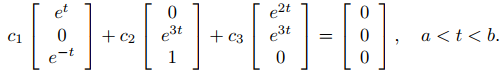
Debemos demostrar que c1 = c2 = c3 = 0. Al reescribir esta ecuación en forma de matriz se obtiene


Ampliando el determinante de este sistema en cofactores de las entradas de la primera fila, se obtiene


Dado que este determinante nunca es cero, c1 = c2 = c3 = 0. ♦
Podemos usar el método del ejemplo 9.10.3.1 para probar n soluciones {y1, y2,. . . , yn} de cualquier sistema n × n y′ = A(t)y para la independencia lineal en un intervalo (a, b) en el que A es continua. Para explicar esto (y para otros propósitos más adelante), es útil escribir una combinación lineal de y1, y2,. . . , yn de una manera diferente. Primero escribimos las funciones vectoriales en términos de sus componentes como


Si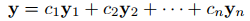
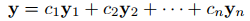


Esto muestra que
c1y1 + c2y2 + · · · + cnyn = Y c, (9.10.3.3)
donde



Para referencia a continuación, tenga en cuenta que


es decir, Y satisface la ecuación diferencial matricial
Y′ = AY.
El determinante de Y,

Teorema 9.10.3.2 [Fórmula de Abel]
Suponga que la matriz cuadrada n × n, A = A(t) es continua en (a, b), y sean y1, y2,. . . , yn soluciones de y′ = A(t)y en (a, b), y un valor particular t0 pertenece al intervalo (a, b). Entonces el wronskiano de {y1, y2,. . . , yn} viene dado por


Por lo tanto, W no tiene ceros en (a, b) o W ≡ 0 en (a, b). ♦
OBSERVACIÓN: La suma de las entradas de la diagonal de una matriz cuadrada A se llama la traza de A, denotada por tr(A). Por lo tanto, para una matriz A de n × n,
tr(A) = a11 + a22 + · · · + ann,
y (9.10.3.6) se puede escribir como
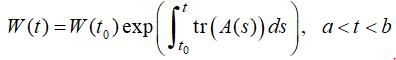
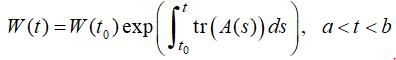
El siguiente teorema es análogo a los teoremas 9.5.1.6 y 9.9.1.4.
Teorema 9.10.3.3
Suponga que la matriz cuadrada n × n, A = A(t) es continua en (a, b), y sean y1, y2,. . . , yn soluciones de y′ = A(t)y en (a, b). Entonces las siguientes declaraciones son equivalentes; es decir, todas son verdaderos o todas son falsas:
(a) La solución general de y′ = A(t)y en (a, b) es y = c1y1 + c2y2 + · · · + cnyn, donde c1, c2,. . ., cn son constantes arbitrarias.
(b) {y1, y2,. . . , yn} es un conjunto fundamental de soluciones de y′ = A(t)y en (a, b).
(c) {y1, y2,. . . , yn} es linealmente independiente en (a, b).
(d) El wronskiano de {y1, y2,. . . , yn} es distinto de cero en algún punto de (a, b).
(e) El wronskiano de {y1, y2,. . . , yn} es distinto de cero en todos los puntos de (a, b). ♦
Decimos que Y en (9.10.3.4) es una matriz fundamental para y′ = A(t)y si alguno (y por lo tanto todos) de los enunciados (a) – (e) del Teorema 9.10.3.2 son verdaderos para las columnas de Y. En este caso, (9.10.3.3) implica que la solución general de y′ = A(t)y se puede escribir como y = Yc, donde c es un n-vector constante arbitrario.
Ejemplo ilustrativo 9.10.3.2
Las funciones vectoriales


son soluciones del sistema de coeficientes constantes
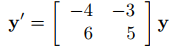
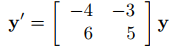
en (−∞, ∞). (Verificar).
(a) Calcule el wronskiano de {y1, y2} directamente de la definición (9.10.3.5)
(b) Verifique la fórmula de Abel (9.10.3.6) para el wronskiano de {y1, y2}.
(c) Encuentre la solución general de (9.10.3.7).
(d) Resuelva el problema de valor inicial


Solución:
(a) De (9.10.3.5)
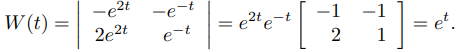
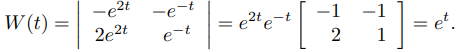
(b) Aquí


entonces tr(A) = −4 + 5 = 1. Si t0 es un número real arbitrario, entonces (9.10.3.6) implica que
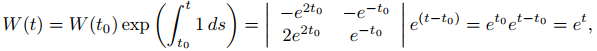
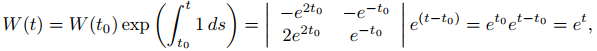
que es consistente con (9.10.3.9).
(c) Dado que W(t) ≠ 0, el teorema 9.10.3.3 implica que {y1, y2} es un conjunto fundamental de soluciones de (9.10.3.7) y
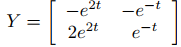
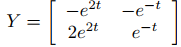
es una matriz fundamental para (9.10.3.7). Por tanto, la solución general de (9.10.3.7) es


(d) Establecer t = 0 en (9.10.3.10) e imponer la condición inicial en (9.10.3.8) produce


Por lo tanto,


La solución de este sistema es c1 = −1, c2 = −3. Sustituyendo estos valores en (9.10.3.10) se obtiene
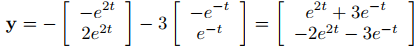
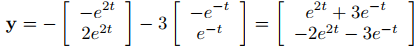
como la solución de (9.10.3.8).
