5. La integral y técnicas de integración

5. La integral y técnicas de integración

La integral

Los barcos de hielo son comunes en los lagos de Wisconsin y Minnesota los fines de semana de invierno. Los botes de hielo son similares a los veleros, pero están equipados con corredores o “patines” y están diseñados para correr sobre el hielo, en lugar de sobre el agua. Los botes de hielo pueden moverse muy rápidamente, y muchos entusiastas de la navegación en hielo se sienten atraídos por el deporte debido a la velocidad. Los mejores corredores de botes de hielo pueden alcanzar velocidades de hasta cinco veces la velocidad del viento. Si sabemos qué tan rápido se mueve un bote de hielo, podemos usar la integración para determinar qué tan lejos viaja. Volveremos sobre esta pregunta más adelante en el capítulo (ver Ejemplo 5.4_5).

Determinar la distancia a partir de la velocidad es solo una de las muchas aplicaciones de la integración. De hecho, las integrales se utilizan en una amplia variedad de aplicaciones mecánicas y físicas. En este capítulo, primero presentamos la teoría detrás de la integración y usamos integrales para calcular áreas. A partir de ahí, desarrollamos el teorema fundamental del cálculo, que relaciona la diferenciación y la integración. Luego estudiamos algunas técnicas básicas de integración y examinamos brevemente algunas aplicaciones.

Técnicas de integración

Figura 5.2 La planificación cuidadosa de las señales de tránsito puede prevenir o reducir la cantidad de accidentes en las intersecciones concurridas. (crédito: modificación del trabajo de David McKelvey, Flickr)

En una ciudad grande, los accidentes ocurrieron a una tasa promedio de uno cada tres meses en una intersección particularmente concurrida. Después de que los residentes se quejaron, se hicieron cambios en los semáforos en la intersección. Han pasado ocho meses desde que se hicieron los cambios y no ha habido accidentes. ¿Fueron efectivos los cambios o es el intervalo de ocho meses sin un accidente un resultado casual? Exploramos esta pregunta más adelante en este capítulo y vemos que la integración es una parte esencial para determinar la respuesta (ver Ejemplo 5.49).

Vemos en el capítulo Aplicaciones de la integral lo importante que puede ser la integración para todo tipo de temas diferentes, desde cálculos de volúmenes hasta caudales, y desde el uso de una función de velocidad para determinar una posición hasta la ubicación de centros de masa. No es sorprendente, entonces, que las técnicas para encontrar antiderivadas (o integrales indefinidas) sean importantes para todos los que las usan. Ya hemos discutido algunas fórmulas básicas de integración y el método de integración por sustitución u. En este capítulo, estudiamos algunas técnicas adicionales, incluidas algunas formas de aproximar integrales definidas cuando las técnicas analíticas normales no funcionan.

Miscelánea de ejercicios del capítulo 5. La integral y técnicas de integración

       En los siguientes ejercicios hallar la integral definida de la función algebraica dada

       En los siguientes ejercicios halle la integral indefinida y verifique el resultado mediante derivación

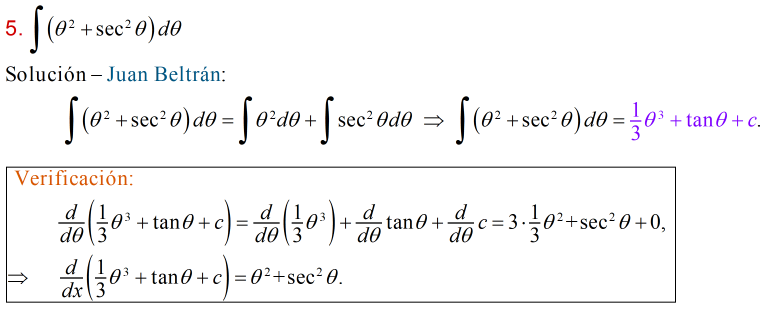
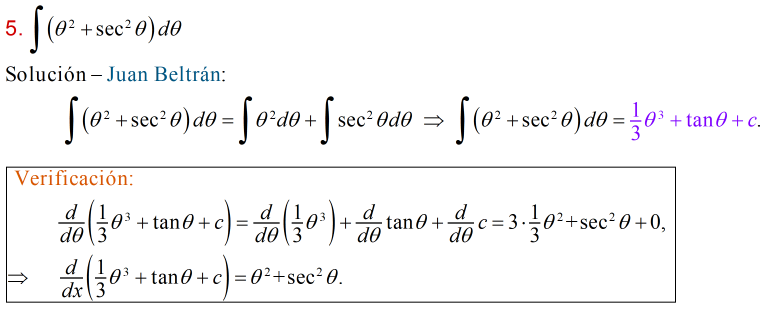
6. Hallar el área de la región delimitada por las ecuaciones y = 5x² + 2, x = 0, x = 2, y = 0

Solución – Juan Beltrán:

El área A de la región se muestra en la siguiente figura

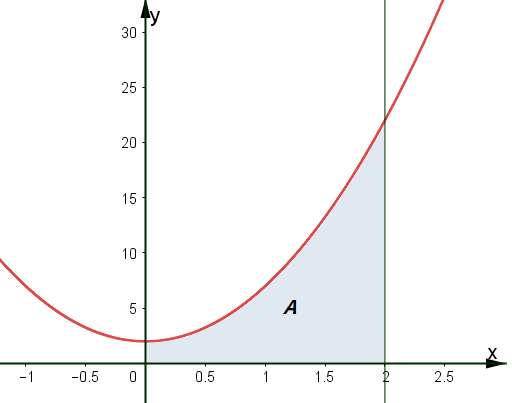
A se calcula mediante la siguiente integral definida

       En los siguientes ejercicios hallar la integral indefinida (antiderivada)