| 4. Aplicaciones de la derivada | Ejercicios propuestos para el capítulo 4.3 |
4.3 MÁXIMOS Y MÍNIMOS
Objetivos de aprendizaje:
4.3.1. Definir extremos absolutos.
4.3.2. Definir extremos locales.
4.3.3. Explicar cómo encontrar los puntos críticos de una función en un intervalo cerrado.
4.3.4. Describa cómo usar puntos críticos para localizar extremos absolutos en un intervalo cerrado.
Dada una función particular, a menudo nos interesa determinar los valores más grandes y más pequeños de la función. Esta información es importante para crear gráficos precisos. Encontrar los valores máximos y mínimos de una función también tiene un significado práctico porque podemos usar este método para resolver problemas de optimización, como maximizar el beneficio, minimizar la cantidad de material utilizado en la fabricación de una lata de aluminio o encontrar la altura máxima que puede alcanzar un cohete. En esta sección, veremos cómo usar derivadas para encontrar los valores más grandes y más pequeños para una función.
Extremo absoluto
Considere la función f (x) = x2 + 1 durante el intervalo (−∞, ∞). Cuando x → ± ∞, f (x) → ∞. Por lo tanto, la función no tiene un valor máximo. Sin embargo, dado que x2 + 1 ≥ 1 para todos los números reales x y x2 + 1 = 1 cuando x = 0, la función tiene el valor más pequeño, 1, cuando x = 0. Decimos que 1 es el mínimo absoluto de f (x) = x2 + 1 y ocurre en x = 0. Decimos que f (x) = x2 + 1 no tiene un máximo absoluto (ver la siguiente figura).
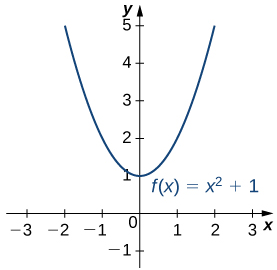
Figura 4.3.1 La función dada tiene un mínimo absoluto de 1 en x = 0. La función no tiene un máximo absoluto.
Definición 4.3.1. Valor máximo y valor mínimo de una función
Sea f una función definida en un intervalo I y sea c∈I. Decimos que f tiene un máximo absoluto de c en I si f (c) ≥ f (x) para todo x∈I. Decimos que f tiene un mínimo absoluto de c en I si f (c) ≤ f (x) para todo x∈I. Si f tiene un máximo absoluto o un mínimo absoluto de c en I , decimos que f tiene un extremo absoluto de c en I . ♦
Antes de continuar, observemos dos cuestiones importantes con respecto a esta definición. Primero, el término absoluto aquí no se refiere al valor absoluto de un número. Un extremo absoluto puede ser positivo, negativo o cero. En segundo lugar, si una función f tiene un extremo absoluto durante un intervalo I en c, el extremo absoluto es f (c). El número real c es un punto en el dominio en el que ocurre el extremo absoluto. Por ejemplo, considere la función f (x) = 1 / (x2 + 1) durante el intervalo (−∞, ∞). Ya que

para todos los números reales x, decimos que f tiene un máximo absoluto sobre (−∞, ∞) en x = 0. El máximo absoluto es f (0) = 1. Ocurre en x = 0, como se muestra en la Figura 4.8 (b).
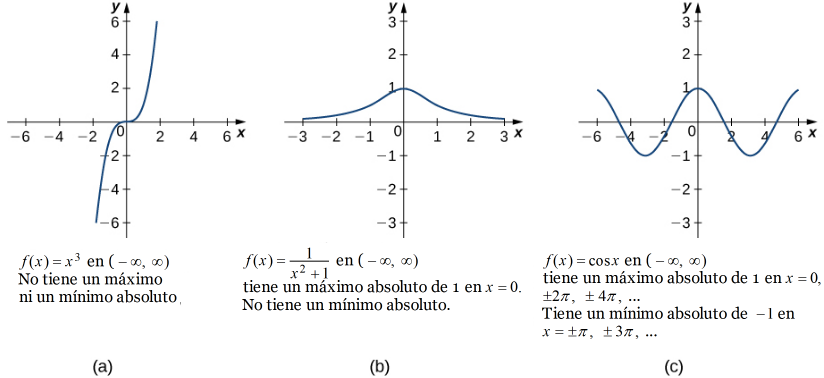
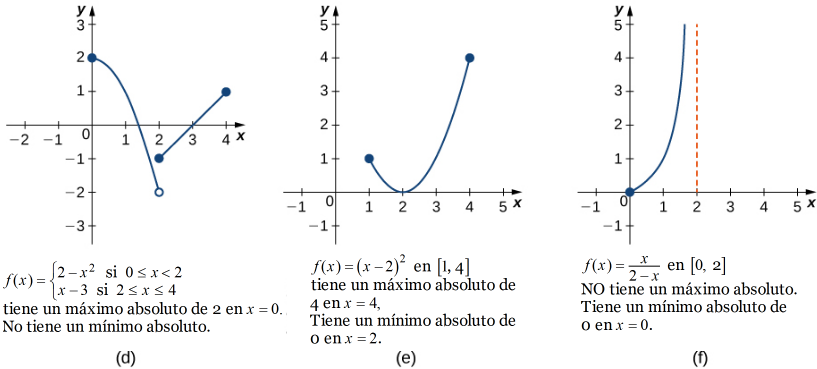
Una función puede tener un máximo absoluto y un mínimo absoluto, solo un extremo, o ninguno. La figura 4.8 muestra varias funciones y algunas de las diferentes posibilidades con respecto a los extremos absolutos. Sin embargo, el siguiente teorema, llamado Teorema del valor extremo, garantiza que una función continua f durante un intervalo cerrado y acotado [a, b] tiene tanto un máximo absoluto como un mínimo absoluto.
Teorema 4.3.1. Teorema del valor extremo
Si f es una función continua sobre el intervalo cerrado y acotado [a, b], entonces hay un punto en [a, b] en el que f tiene un máximo absoluto sobre [a, b], y hay un punto en [a, b], en el que f tiene un mínimo absoluto sobre [a, b]. ♦
La demostración del teorema del valor extremo está más allá del alcance de este texto. Por lo general, se demuestra en un curso sobre análisis real. Hay un par de puntos clave a tener en cuenta sobre el enunciado de este teorema. Para que se aplique el teorema del valor extremo, la función debe ser continua durante un intervalo cerrado y acotado. Si el intervalo I está abierto o la función tiene incluso un punto de discontinuidad, es posible que la función no tenga un máximo absoluto o un mínimo absoluto sobre I. Por ejemplo, considere las funciones que se muestran en la Figura 4.8 (d), (e) y ( F). Las tres funciones se definen en intervalos limitados. Sin embargo, la función en el gráfico (e) es la única que tiene un máximo absoluto y un mínimo absoluto sobre su dominio. El teorema del valor extremo no se puede aplicar a las funciones en los gráficos (d) y (f) porque ninguna de estas funciones es continua durante un intervalo cerrado y acotado. Aunque la función en el gráfico (d) se define durante el intervalo cerrado [0,4], la función es discontinua en x = 2. La función tiene un máximo absoluto sobre [0,4] pero no tiene un mínimo absoluto. La función en el gráfico (f) es continua durante el intervalo medio abierto [0,2), pero no está definida en x = 2 y, por lo tanto, no es continua durante un intervalo cerrado y acotado. La función tiene un mínimo absoluto sobre [0,2), pero no tiene un máximo absoluto sobre [0,2). Estos dos gráficos ilustran por qué una función en un intervalo acotado puede no tener un máximo absoluto y / o un mínimo absoluto.
Antes de ver cómo encontrar extremos absolutos, examinemos el concepto relacionado de extremos locales. Esta idea es útil para determinar dónde ocurren los extremos absolutos.
Extremo local y puntos críticos
Considere la función f que se muestra en la figura 4.9. La gráfica se puede describir como dos montañas con un valle en el medio. El valor máximo absoluto de la función ocurre en el pico más alto, en x = 2. Sin embargo, x = 0 también es un punto de interés. Aunque f (0) no es el valor más grande de f, el valor f (0) es mayor que f (x) para todas las x cercanas a 0. Decimos que f tiene un máximo local en x = 0. De manera similar, la función f no tiene un mínimo absoluto, pero sí tiene un mínimo
local en x = 1 porque f (1) es menor que f (x) para tica x cerca de 1.

Definición 4.3.2. Extremos locales
Una función f tiene un máximo local en c si existe un intervalo abierto I que contiene a c de modo que esté contenido en el dominio de f y f (c) ≥ f (x) para todo x∈I. Una función f tiene un mínimo local en c si existe un intervalo abierto I que contiene a c de modo que esté contenido en el dominio de f y f (c) ≤ f (x) para todo x∈I. Una función f tiene un extremo local en c si f tiene un máximo local en c o f tiene un mínimo local en c. ♦
Tenga en cuenta que si f tiene un extremo absoluto en c y f
se define en un intervalo que contiene c, entonces f (c) también se considera un extremo local. Si un extremo absoluto para una función f ocurre en un punto final, no consideramos que sea un extremo local, sino que lo llamamos punto final extremo.
Dada la gráfica de una función f, a veces es fácil ver dónde se produce un máximo local o un mínimo local. Sin embargo, no siempre es fácil de ver, ya que las características interesantes en la gráfica de una función pueden no ser visibles porque ocurren a una escala muy pequeña. Además, es posible que no tengamos una gráfica de la función. En estos casos, ¿cómo podemos usar una fórmula para una función para determinar dónde ocurren estos extremos?
Para responder a esta pregunta, veamos nuevamente la Figura 4.9. Los extremos locales ocurren en x = 0, x = 1 y x = 2. Observe que en x = 0 y x = 1, la derivada f ‘(x) = 0. En x = 2, la derivada f ‘(x) no existe, ya que la función f tiene una esquina allí. De hecho, si f tiene un extremo local en un punto x = c, la derivada f ‘(c) debe cumplir una de las siguientes condiciones: f ‘ (c) = 0 o f ‘(c) no está definida. Tal valor c se conoce como un número crítico y es importante para encontrar valores extremos para las funciones.
Definición 4.3.3. Número crítico
Sea c un número (punto) interior en el dominio de f. Decimos que c es un número crítico (o punto crítico) de f si f ‘(c) = 0 o f ‘ (c) no está definido. ♦
Como se mencionó anteriormente, si f tiene un extremo local en un punto x = c, entonces c debe ser un punto crítico de f. Este hecho se conoce como el teorema de Fermat.
Teorema 4.3.2. Teorema de Fermat
Si f tiene un extremo local en c y f es diferenciable en c, entonces f ′(c) = 0. ♦
Prueba:
Suponga que f tiene un extremo local en c y f es diferenciable en c. Necesitamos mostrar que f ‘(c) = 0. Para hacer esto, mostraremos que f ‘(c) ≥ 0 y f ‘ (c) ≤0, y por lo tanto f ‘(c) = 0. Como f tiene un extremo local en c, f tiene un máximo local o un mínimo local en c. Supongamos que f tiene un máximo local en c. El caso en el que f tiene un mínimo local en c puede manejarse de manera similar. Entonces existe un intervalo abierto I tal que f (c) ≥ f (x) para todo x∈I. Como f es diferenciable en c, de la definición de la derivada, sabemos que
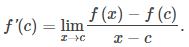
Dado que este límite existe, también existen los límites unilaterales e iguales f ‘(c). Por lo tanto,

y
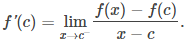
Como f (c) es un máximo local, vemos que f (x) − f (c) ≤ 0 para x cerca de c. Por lo tanto, para x cerca de c, pero x > c, tenemos [f (x) − f (c)]/(x − c) ≤ 0. De la ecuación (1) concluimos que f ′(c) ≤ 0. Del mismo modo, se puede demostrar que f ′(c) ≥ 0. Por lo tanto, f ′(c) = 0. ♦
Del teorema de Fermat, concluimos que si f tiene un extremo local en c, entonces f ′(c) = 0 o f ′(c) no está definido. En otras palabras, los extremos locales solo pueden ocurrir en puntos críticos. Tenga en cuenta que este teorema no afirma que una función f debe tener un extremo local en un punto crítico. Más bien, establece que los puntos críticos son candidatos para extremos locales. Por ejemplo, considere la función f (x) = x3. Tenemos f ′(x) = 3x2 = 0 cuando x = 0. Por lo tanto, x = 0 es un punto crítico. Sin embargo, f (x) = x3 es monótona creciente en (−∞, ∞), y por lo tanto f no tiene un extremo local en x = 0. En la figura 4.10, vemos varias posibilidades diferentes para puntos críticos. En algunos de estos casos, las funciones tienen extremos locales en puntos críticos, mientras que en otros casos no. Tenga en cuenta que estos gráficos no muestran todas las
posibilidades para el comportamiento de una función en un punto crítico.

Más adelante en este capítulo, analizamos los métodos analíticos para determinar si una función realmente tiene un extremo local en un punto crítico. Por ahora, centramos nuestra atención en encontrar puntos críticos. Usaremos observaciones gráficas para determinar si un punto crítico está asociado con un extremo local.
Ejemplo ilustrativo 4.3.1: Localizando Puntos Críticos
Para cada una de las siguientes funciones, encuentra todos los puntos críticos. Usa una utilidad de graficación para determinar si la función tiene un extremo local en cada uno de los puntos críticos.
a. \(f(x) = \frac{1}{3}x^3 – \frac{5}{2}x^2 + 4x\)
b. \(f(x) = (x^2 – 1)^3\)
c. \(f(x) = \frac{4x}{1 + x^2}\)
Solución:
a. La derivada \(f'(x) = x^2 – 5x + 4\) está definida para todos los números reales \(x\). Por lo tanto, solo necesitamos encontrar los valores de \(x\) donde \(f'(x) = 0\). Dado que \(f'(x) = x^2 – 5x + 4 = (x – 4)(x – 1)\), los puntos críticos son \(x = 1\) y \(x = 4\). De la gráfica de \(f\) en la Figura 4.3.5, vemos que \(f\) tiene un máximo local en \(x = 1\) y un mínimo local en \(x = 4\).
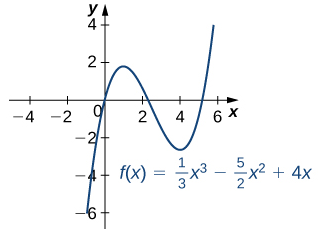
Figura 4.3.5 Esta función tiene un máximo local y un mínimo local.
b. Usando la regla de la cadena, vemos que la derivada es
\[ f'(x) = 3(x^2 – 1)^2(2x) = 6x(x^2 – 1)^2. \]Por lo tanto, \(f\) tiene puntos críticos cuando \(x = 0\) y cuando \(x^2 – 1 = 0\). Concluimos que los puntos críticos son \(x = 0, \pm 1\). De la gráfica de \(f\) en la Figura 4.3.6, vemos que \(f\) tiene un mínimo local (y absoluto) en \(x = 0\), pero no tiene un extremo local en \(x = 1\) o \(x = -1\).
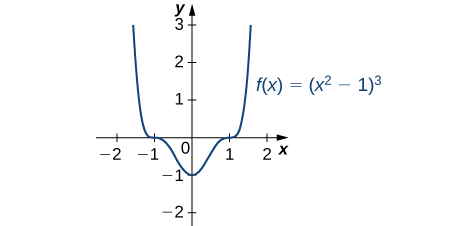
Figura 4.3.6 Esta función tiene tres puntos críticos: x = 0, x = 1 y x = -1. La función tiene un mínimo local (y absoluto) en x = 0, pero no tiene extremos en los otros dos puntos críticos.
c. Mediante la regla del cociente, vemos que la derivada es
\[ f'(x) = \frac{(1 + x^2)(4) – 4x(2x)}{(1 + x^2)^2} = \frac{4 – 4x^2}{(1 + x^2)^2}. \]La derivada está definida en todas partes. Por lo tanto, solo necesitamos encontrar los valores de \(x\) donde \(f'(x) = 0\). Resolviendo \(f'(x) = 0\), vemos que \(4 – 4x^2 = 0\), lo que implica \(x = \pm 1\). Por lo tanto, los puntos críticos son \(x = \pm 1\). De la gráfica de \(f\) en la Figura 4.3.7, vemos que \(f\) tiene un máximo absoluto en \(x = 1\) y un mínimo absoluto en \(x = -1\). Por lo tanto, \(f\) tiene un máximo local en \(x = 1\) y un mínimo local en \(x = -1\). (Nótese que si \(f\) tiene un extremo absoluto sobre un intervalo \(I\) en un punto \(c\) que no es un punto extremo de \(I\), entonces \(f\) tiene un extremo local en \(c\).)
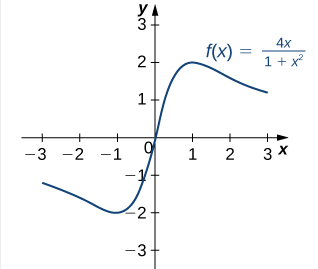
Figura 4.3.7 Esta función tiene un máximo absoluto y un mínimo absoluto. ♦
Ejercicio de control 4.3.1
Encuentra todos los puntos críticos para \(f(x) = x^3 – \frac{1}{2}x^2 – 2x + 1\). ♦
Localizando Extremos Absolutos
El teorema del valor extremo establece que una función continua en un intervalo cerrado y acotado tiene un máximo absoluto y un mínimo absoluto. Como se muestra en la Figura 4.8, uno o ambos de estos extremos absolutos podrían ocurrir en un punto final. Sin embargo, si un extremo absoluto no ocurre en un punto final, debe ocurrir en un punto interior, en cuyo caso el extremo absoluto es un extremo local. Por lo tanto, según el teorema de Fermat, el punto c en el que se produce el extremo local debe ser un punto crítico. Resumimos este resultado en el siguiente teorema.
Teorema 4.3.4. Ubicación de Extremos Absolutos
Sea f una función continua sobre un intervalo cerrado, acotado I. El máximo absoluto de f sobre I y el mínimo absoluto de f sobre I debe ocurrir en los puntos finales de I o en los puntos críticos de f en I. ♦
Con esta idea en mente, examinemos un procedimiento para localizar extremos absolutos.
Estrategia de resolución de problemas: localización de extremos absolutos sobre un intervalo cerrado
Considere una función continua f definida en el intervalo cerrado [a, b].
- Evalúe f en los puntos finales x = a y x = b.
- Encuentre todos los puntos críticos de f que se encuentran sobre el intervalo (a, b) y evalúe f en esos puntos críticos.
- Compare todos los valores encontrados en (1) y (2). Tenga presente que los extremos absolutos deben ocurrir en puntos finales o puntos críticos. Por lo tanto, el mayor de estos valores es el máximo absoluto de f. El más pequeño de estos valores es el mínimo absoluto de f.
Ahora veamos cómo usar esta estrategia para encontrar los valores máximos y mínimos absolutos de funciones continuas.
Ejemplo ilustrativo 4.3.2: Localización de Extremos Absolutos
Para cada una de las siguientes funciones, encuentra el máximo absoluto y el mínimo absoluto sobre el intervalo especificado e indica dónde ocurren esos valores.
a. \(f(x) = -x^2 + 3x – 2\) sobre \([1, 3]\).
b. \(f(x) = x^2 – 3x^{\frac{2}{3}}\) sobre \([0, 2]\).
Solución:
a. Paso 1. Evaluar \(f\) en los puntos extremos \(x = 1\) y \(x = 3\).
\[ f(1) = 0 \text{ y } f(3) = -2 \]Paso 2. Dado que \(f'(x) = -2x + 3\), \(f’\) está definida para todos los números reales \(x\). Por lo tanto, no hay puntos críticos donde la derivada sea indefinida. Queda comprobar dónde \(f'(x) = 0\). Dado que
\[ f'(x) = -2x + 3 = 0 \text{ en } x = \frac{3}{2} \]y \(\frac{3}{2}\) está en el intervalo \([1, 3]\), \(f\left(\frac{3}{2}\right)\) es un candidato para un extremo absoluto de \(f\) sobre \([1, 3]\). Evaluamos \(f\left(\frac{3}{2}\right)\) y encontramos
\[ f\left(\frac{3}{2}\right) = \frac{1}{4}. \]Paso 3. Configuramos la siguiente tabla para comparar los valores encontrados en los pasos 1 y 2.
| \(x\) | \(f(x)\) | Conclusión |
|---|---|---|
| 1 | 0 | |
| \(\frac{3}{2}\) | \(\frac{1}{4}\) | Máximo absoluto |
| 3 | -2 | Mínimo absoluto |
De la tabla, encontramos que el máximo absoluto de \(f\) sobre el intervalo \([1, 3]\) es \(\frac{1}{4}\), y ocurre en \(x = \frac{3}{2}\). El mínimo absoluto de \(f\) sobre el intervalo \([1, 3]\) es \(-2\), y ocurre en \(x = 3\) como se muestra en la siguiente gráfica.
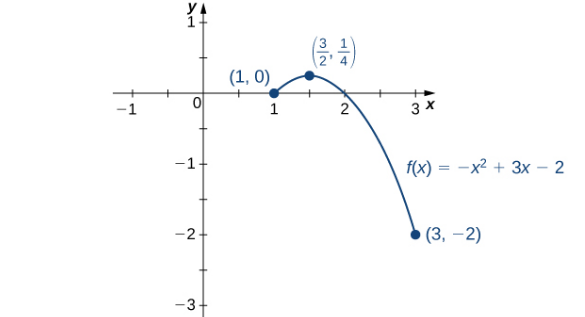
Figura 4.3.8 Esta función tiene tanto un máximo absoluto como un mínimo absoluto.
b. Paso 1. Evaluar \(f\) en los puntos extremos \(x = 0\) y \(x = 2\).
\[ f(0) = 0 \text{ y } f(2) = 4 – 3\sqrt[3]{4} \approx -0.762 \]Paso 2. La derivada de \(f\) está dada por
\[ f'(x) = 2x – \frac{2}{x^{\frac{1}{3}}} = \frac{2x^{\frac{4}{3}} – 2}{x^{\frac{1}{3}}} \]para \(x \ne 0\). La derivada es cero cuando \(2x^{\frac{4}{3}} – 2 = 0\), lo cual implica \(x = \pm 1\). La derivada es indefinida en \(x = 0\). Por lo tanto, los puntos críticos de \(f\) son \(x = 0, 1, -1\). El punto \(x = 0\) es un punto extremo, así que ya evaluamos \(f(0)\) en el paso 1. El punto \(x = -1\) no está en el intervalo de interés, así que solo necesitamos evaluar \(f(1)\). Encontramos que
\[ f(1) = -2. \]Paso 3. Comparamos los valores encontrados en los pasos 1 y 2, en la siguiente tabla.
| \(x\) | \(f(x)\) | Conclusión |
|---|---|---|
| 0 | 0 | Máximo absoluto |
| 1 | -2 | Mínimo absoluto |
| 2 | -0.762 |
Concluimos que el máximo absoluto de \(f\) sobre el intervalo \([0, 2]\) es cero, y ocurre en \(x = 0\). El mínimo absoluto es -2, y ocurre en \(x = 1\) como se muestra en la siguiente gráfica.
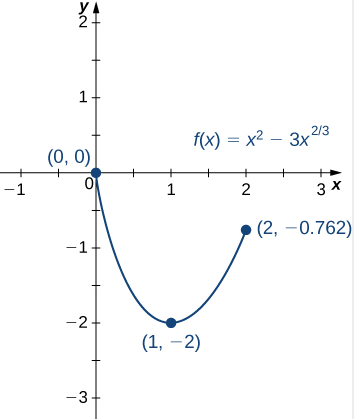
Figura 4.3.9 Esta función tiene un máximo absoluto en un extremo del intervalo.
Ejercicio de control 4.3.2
Encuentra el máximo absoluto y el mínimo absoluto de \(f(x) = x^2 – 4x + 3\) sobre el intervalo \([1, 4]\). ♦
En este punto, sabemos cómo localizar extremos absolutos para funciones continuas sobre intervalos cerrados. También hemos definido extremos locales y determinado que si una función \(f\) tiene un extremo local en un punto \(c\), entonces \(c\) debe ser un punto crítico de \(f\). Sin embargo, que \(c\) sea un punto crítico no es una condición suficiente para que \(f\) tenga un extremo local en \(c\). Más adelante en este capítulo, mostraremos cómo determinar si una función realmente tiene un extremo local en un punto crítico. Primero, sin embargo, necesitamos introducir el Teorema del Valor Medio, que nos ayudará a analizar el comportamiento de la gráfica de una función.

Sus documentos me parecen excelentes. >Espero poder apoyarme en ellos para conocimientos necesarios de los temas de matemática. Felicidades
Bienvenida. Más adelante voy a subir los Ejercicios resueltos y propuestos sobre este importante tema. 👀👍🏻