| 1. Funciones y sus gráficas |

1.1. Revisión de funciones: Objetivos de aprendizaje

1.1.1. Usar la notación funcional para evaluar una función.
1.1.2. Determinar el dominio y el rango de una función.
1.1.3. Trazar la gráfica de una función.
1.1.4. Calcular los ceros de una función.
1.1.5. Reconocer una función de una tabla de valores.
1.1.6. Construir nuevas funciones a partir de dos o más funciones dadas.
1.1.7. Describir las propiedades de simetría de una función

| Ejercicios propuestos para Capítulo 1.1 | Ejercicios resueltos del Capítulo 1 |

    En esta sección, se da una definición formal de función y examinamos varias formas en que se representan las funciones; a través de tablas, fórmulas y gráficas. Estudiamos la notación formal y los términos relacionados con las funciones. También definimos la composición de funciones y las propiedades de simetría de una función.

Las funciones se usan todo el tiempo en matemáticas para describir las relaciones entre dos conjuntos. Para cualquier función, cuando conocemos la entrada, se determina la salida, por lo que decimos que la salida es una función de la entrada. Por ejemplo, el área de un círculo está determinada por la longitud de su radio, por lo que decimos que el área del círculo (la salida) es una función de la longitud del radio (la entrada).

Concepto de función

Sean dos conjuntos A y B, entonces el conjunto de pares ordenados (x, y), donde x es un elemento del conjunto A y y es un elemento del conjunto B, se dice que es una relación de A a B. Una función es un tipo especial de relación en la que cada elemento del primer conjunto está relacionado con exactamente un elemento del segundo conjunto. El elemento del primer conjunto se llama entrada ; el elemento del segundo conjunto se llama salida.

Definición 1.1_1. Definición de función

Una función f consiste en un conjunto de entradas, un conjunto de salidas y una regla para asignar cada entrada a exactamente una salida. El conjunto de entradas se denomina dominio de la función. El conjunto de salidas se denomina rango de la función.

Por ejemplo, considere la función f, donde el dominio es el conjunto de todos los números reales y la regla de correspondencia es elevar al cuadrado la entrada. Entonces, la entrada x = 3 se asigna a la salida 3²  =  9. Dado que cada número real no negativo tiene una raíz cuadrada de valor real, cada número no negativo es un elemento del rango de esta función. Como no hay un número real con un cuadrado que sea negativo, los números reales negativos no son elementos del rango. Concluimos que el rango es el conjunto de números reales no negativos.

Para una función general con dominio D, a menudo usamos x para denotar la entrada e y para denotar la salida asociada con x. Al hacerlo, nos referimos a x como la variable independiente y a y como la variable dependiente, porque depende de x. Usando la notación de función, escribimos y = f (x), y leemos esta ecuación como “y es igual a f de x”. Para la función de “elevar al cuadrado” dada en el ejemplo anterior, escribimos f (x) = x².

El concepto de función se puede visualizar mediante los siguientes esquemas:

Fig.1.1_1 Una función se puede visualizar como un dispositivo de entrada/salida

Fig.1.1_2 Una función asigna cada elemento en el dominio a exactamente un elemento en el rango. Aunque cada entrada se debe enviar a una sola salida, se pueden enviar dos entradas diferentes a la misma salida.

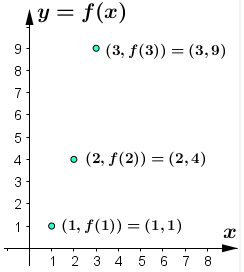
Fig.1.1_3 Se tiene la gráfica de la función f (x) = x², con dominio el conjunto {1, 2, 3} y rango {1, 4, 9}. La variable independiente es x y la variable dependiente es y.

Dominio y rango y su notación

Cada función tiene un dominio. Sin embargo, a veces una función se describe mediante una ecuación, como en f (x) = x², sin un dominio específico dado. En este caso, se considera que el dominio es el conjunto de todos los números reales x para los cuales f (x) es un número real. Por ejemplo, dado que cualquier número real se puede elevar al cuadrado, si no se especifica ningún otro dominio, consideramos que el dominio de f (x) = x²  es el conjunto de todos los números reales. Por otro lado, la función de raíz cuadrada f(x) = √x solo da una salida real si x no es negativa. Por lo tanto, el dominio de la función f (x) = √x es el conjunto de números reales no negativos, a veces llamado dominio natural.

Para las funciones f (x) = x²  y f (x) = √x, los dominios son conjuntos con un número infinito de elementos. Claramente no podemos enumerar todos estos elementos. Al describir un conjunto con un número infinito de elementos, a menudo es útil usar la notación de conjuntos o la notación de intervalo. Cuando se usa la notación de conjuntos para describir un subconjunto de todos los números reales, denotado por ℝ, escribimos

{x | x tiene alguna propiedad}.

Leemos lo anterior como “el conjunto de números reales x, tal que x tiene alguna propiedad”.

Por ejemplo, si estuviéramos interesados en el conjunto de números reales que son mayores que dos pero menores que siete, podríamos denotar este conjunto utilizando la notación de conjuntos escribiendo

{x | 2 < x < 7}.

Los números 2 y 7 se denominan extremos de este conjunto. Si queremos considerar el conjunto que incluye los extremos, denotaremos este conjunto escribiendo, en la notación de intervalos y en la notación de conjuntos respectivamente,

[2, 7] = {x | 2 ≤ x ≤ 7}.

Podemos usar una notación similar si queremos incluir uno de los extremos, pero no el otro.

(2, 7] = {x | 2 < x ≤ 7}

[2, 7) = {x | 2 ≤ x < 7}.

Para denotar el conjunto de números reales no negativos, utilizamos la notación de conjuntos

{x | 0 ≤ x}.

El número más pequeño en este conjunto es cero, pero este conjunto no tiene un número más grande.

Usando la notación de intervalo, usamos el símbolo ∞, que se refiere al infinito positivo, y escribiríamos el conjunto como

[0, ∞) = {x | 0 ≤ x}.

Es importante tener en cuenta que ∞ no es un número real. Aquí se usa simbólicamente para indicar que este conjunto incluye todos los números reales mayores o iguales a cero. Del mismo modo, si quisiéramos describir el conjunto de todos los números no positivos, podríamos escribir

(−∞, 0] = {x | x ≤ 0}.

Aquí, la notación −∞ se refiere al infinito negativo, e indica que estamos incluyendo todos los números menores o iguales a cero, sin importar cuán pequeños sean.

El conjunto (−∞, ∞) = {x | x es cualquier número real} se refiere al conjunto de todos los números reales.

Funciones definidas por tramos

Algunas funciones se definen usando diferentes ecuaciones para diferentes partes de su dominio. Estos tipos de funciones se conocen como funciones definidas por tramos. Por ejemplo, supongamos que queremos definir una función f con un dominio que es el conjunto de todos los números reales de modo que f (x) = 2x – 4 para x  ≤  1  y  f (x) = x³ + 1 para x > 1. Denotamos esta función escribiendo

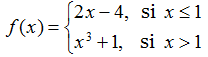
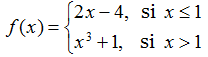
Al evaluar esta función para una entrada x, la ecuación a usar depende de si x ≤ 1 o x > 1. Por ejemplo, como 3 > 1, usamos el hecho de que f (x) = x³ + 1 para x > 1 y vemos que f (3) = 3³ + 1 = 28. Por otro lado, para x = −1, usamos el hecho de que  f (x) = 2x − 4 para x ≤ 1 y vemos que f (−1) = − 6.

EJEMPLO ILUSTRATIVO 1.1_1. Evaluando funciones

Para la función f (x) = 3x² + 2x − 1, evalúe
a.  f (−2)
b.  f (√2)
c.  f (a + h)

Solución:
Sustituya el valor dado para x en la fórmula para f (x) y efectué las operaciones aritméticas que quedan indicadas:

Ejercicio de control 1.1_1

Para f (x) = x² − 3x + 5, evalúe f (1) y f (a + h).

EJEMPLO ILUSTRATIVO 1.1_2. Encontrar dominio y rango

Para cada una de las siguientes funciones, determine el i. dominio y ii. rango.

a.  f (x) = (x − 4)² + 5
b.  f (x) = √(3x + 2) − 1
c. f (x) = 3/(x − 2)

Solución:
a.  Considere f (x) = (x − 4)² + 5.
          i.  Como f (x) = (x − 4)² + 5 es un número real para cualquier número real x, el dominio de f es el intervalo (−∞, ∞).   

        ii. Como (x − 4)² ≥ 0, deducimos que f (x) = (x − 4)² + 5 ≥ 5. Por lo tanto, el rango debe ser un subconjunto de {y| y ≥ 5}. Para mostrar que cada elemento de este conjunto está en el rango, debemos mostrar que para una y dada en ese conjunto, hay un número real x tal que f (x) = (x − 4)² + 5 = y. Al resolver esta ecuación para x, vemos que necesitamos x tal que

(x − 4)² = y − 5.

Esta ecuación se cumple siempre que exista un número real x tal que

x − 4 = ± √(y − 5). 

Para y ≥ 5, la raíz cuadrada está bien definida. Concluimos que para x = 4 ± √(y − 5), f (x) = y, y por lo tanto el rango es {y|y ≥ 5}.

b.  Considere f (x) = √(3x + 2) − 1.

   i.  Para encontrar el dominio de f, necesitamos la expresión 3x + 2 ≥ 0. Al resolver esta desigualdad, concluimos que el dominio es {x|x ≥ − 2/3}.

    ii. Para encontrar el rango de f, observamos que como √(3x + 2) ≥ 0, f (x) = 3√(3x + 2) − 1 ≥ − 1. Por lo tanto, el rango de f debe ser un subconjunto del conjunto {y|y ≥ − 1}. Para mostrar que todos los elementos de este conjunto están en el rango de f, debemos mostrar que para todos los y en este conjunto, existe un número real x en el dominio tal que f (x) = y. Deje y ≥ − 1. Entonces, f (x) = y si y solo si

 3√(3x + 2) − 1 = y.

Al resolver esta ecuación para x, vemos que x debe resolver la ecuación

 3√(3x + 2) = y + 1.

Debido a que y ≥ − 1, tal x podría existir. Al elevar al cuadrado ambos lados de esta ecuación, tenemos 3x + 2 = (y + 1)².
Por lo tanto, necesitamos

3x = (y + 1)² − 2,

lo que implica

x = (1/3) (y + 1)² − 2/3.

Solo necesitamos verificar que x esté en el dominio de f. Dado que el dominio de f consiste en todos los números reales mayores o iguales a −2/3, y

(1/3) (y + 1)² − 2/3 ≥ − 2/3,

existe una x en el dominio de f. Concluimos que el rango de f es {y|y ≥ − 1}.

c. Considere f (x) = 3 / (x − 2).
          i.  Como 3 / (x − 2) se define cuando el denominador es distinto de cero, el dominio es {x| x ≠ 2}.
        ii. Para encontrar el rango de f, necesitamos encontrar los valores de y de modo que exista un número real x en el dominio con la propiedad que

3/(x − 2) = y.

Resolviendo esta ecuación para x, encontramos que

x = 3/y + 2. 

Por lo tanto, mientras y ≠ 0, existe un número real x en el dominio tal que f (x) = y. Por lo tanto, el rango es {y | y ≠ 0}.

Ejercicio de control 1.1_2

Encuentre el dominio y el rango para la función f (x) = √(4 − 2x) + 5.