| 9. Ecuaciones diferenciales | 9.2. Ecuaciones diferenciales de primer orden |
9.2.3 Existencia y unicidad de soluciones de ecuaciones no lineales
Aunque existen métodos para resolver algunas ecuaciones no lineales, es imposible encontrar fórmulas útiles para las soluciones de la mayoría. Ya sea que estemos buscando soluciones exactas o aproximaciones numéricas, es útil conocer las condiciones que implican la existencia y unicidad de soluciones de problemas de valor inicial para ecuaciones no lineales. En esta sección establecemos tal condición y la ilustramos con ejemplos.
Rectángulo abierto
Alguna terminología: un rectángulo abierto R es un conjunto de puntos (x, y) tales que
a < x < b y c < y < d
(Figura 9.2.3_1). Denotaremos este conjunto por R: {a < x < b, c < y < d}. “Abierto” significa que el límite (perímetro) del rectángulo (indicado por las líneas discontinuas en la figura 9.2.3_1) no está incluido en R.
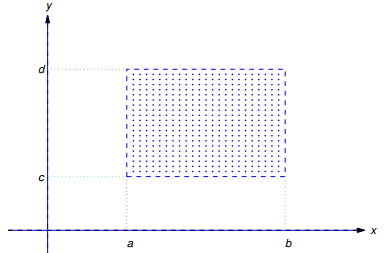

Figura 9.2.3_1 Un rectángulo abierto
El siguiente teorema proporciona condiciones suficientes para la existencia y unicidad de las soluciones de problemas de valor inicial para ecuaciones diferenciales no lineales de primer orden. Omitimos la prueba, que está más allá del alcance de este libro.
Teorema 9.2.3.1
(a) Si f es una función continua en un rectángulo abierto
R: {a < x < b, c < y < d},
que contiene al punto (x₀, y₀), entonces el problema de valor inicial
y′ = f (x, y), y(x₀) = y₀ (9.2.3.1)
tiene al menos una solución en algún subintervalo abierto de (a, b) que contiene a x₀.
(b) Si tanto f como fy (derivada parcial de f respecto a y) son continuas en R, entonces (9.2.3.1) tiene una solución única en algún subintervalo abierto de (a, b) que contiene a x₀. ♦
Es importante comprender exactamente lo que dice el Teorema 9.2.3.1.
- (a) Es un teorema de existencia. Garantiza que existe una solución en algún intervalo abierto que contiene a x₀, pero no proporciona información sobre cómo encontrar la solución o determinar el intervalo abierto en el que existe. Además, (a) no proporciona información sobre el número de soluciones que (9.2.3.1) puede tener. Deja abierta la posibilidad de que (9.2.3.1) pueda tener dos o más soluciones que difieran para valores de x arbitrariamente cercanos a x₀. Veremos en el ejemplo 9.2.3_6 que esto puede suceder.
- (b) Es un teorema de unicidad. Garantiza que (9.2.3.1) tiene una solución única en algún intervalo abierto (a, b) que contiene a x₀. Sin embargo, si (a, b) ≠ (−∞, ∞), (9.2.3.1) puede tener más de una solución en un intervalo mayor que contiene a (a, b). Por ejemplo, puede suceder que b < ∞ y todas las soluciones tengan los mismos valores en (a, b), pero dos soluciones y₁ e y₂ están definidas en algún intervalo (a, b₁) con b₁ > b, y tienen valores diferentes para b < x < b₁; por lo tanto, las gráficas de y₁ e y₂ se “ramifican” en diferentes direcciones en x = b. (Consulte el ejemplo 9.2.3_7 y la figura 9.2.3.3). En este caso, la continuidad implica que y₁(b) = y₂(b) (llame a su valor común ӯ), y y₁ e y₂ son ambas soluciones del problema del valor inicial
y′ = f (x, y), y(b) = ӯ (9.2.3.2)
- que difieren en cada intervalo abierto que contiene b. Por lo tanto, f o fy debe tener una discontinuidad en algún punto de cada rectángulo abierto que contiene (b, ӯ), ya que si esto no fuera así, (9.2.3.2) tendría una solución única en algún intervalo abierto que contenga b. Te dejamos dar un análisis similar del caso donde a > −∞.
Ejemplo ilustrativo 9.2.3_1
Considere el problema de valor inicial


Ya que


son continuas para todo (x, y), el teorema 9.2.3.1 implica que si (x₀, y₀) es arbitrario, entonces este problema de valor inicial tiene una solución única en algún intervalo abierto que contiene a x₀. ♦
Ejemplo ilustrativo 9.2.3_2
Considere el problema de valor inicial


Aquí


son continuas en todas partes excepto en (0, 0). Si (x₀, y₀) ≠ (0, 0), hay un rectángulo abierto R que contiene a (x₀, y₀) que no contiene (0, 0). Dado que f y fy son continuas en R, el teorema 9.2.3.1 implica que si (x₀, y₀) ≠ (0, 0) entonces este problema de valor inicial tiene una solución única en algún intervalo abierto que contiene a x₀. ♦
Ejemplo ilustrativo 9.2.3_3
Considere el problema de valor inicial
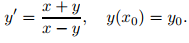
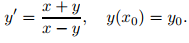
Aquí


son continuas en todas partes excepto en la recta y = x. Si y₀ ≠ x₀, hay un rectángulo abierto R que contiene (x₀, y₀) que no cruza la recta y = x. Dado que f y fy son continuas en R, el teorema 9.2.3.1 implica que si y₀ ≠ x₀, este problema de valor inicial tiene una solución única en algún intervalo abierto que contiene a x₀. ♦
Ejemplo ilustrativo 9.2.3_4
En el ejemplo 9.2.2_4 vimos que las soluciones de
y′ = 2xy² (9.2.3.6)
son
y ≡ 0 y y = −1/(x² + c),
donde c es una constante arbitraria. En particular, esto implica que ninguna solución de y′ = 2xy² distinta de y ≡ 0 puede ser igual a cero para cualquier valor de x. Demuestre que el teorema 9.2.3.1 (b) implica esto.
Solución:
Obtendremos una contradicción asumiendo que la ecuación y′ = 2xy² tiene una solución y₁ que es igual a cero para algún valor de x, pero no es idénticamente cero. Si y₁ tiene esta propiedad, hay un punto x₀ tal que y₁(x₀) = 0, pero y₁(x) ≠ 0 para algún valor de x en cada intervalo abierto que contiene x₀. Esto significa que el problema de valor inicial
y′ = 2xy², y(x₀) = 0 (9.2.3.7)
tiene dos soluciones y ≡ 0 e y = y₁ que difieren para algún valor de x en cada intervalo abierto que contiene x₀. Lo anterior contradice el teorema 9.2.3.1(b), ya que en y′ = 2xy² las funciones


son ambas continuas para todo (x, y), lo que implica que el PVI y′ = 2xy², y(x₀) = 0 tiene una solución única en algún intervalo abierto que contiene a x₀. ♦
Ejemplo ilustrativo 9.2.3_5
Considere el problema de valor inicial


(a) ¿Para qué puntos (x₀, y₀) el teorema 9.2.3.1 (a) implica que este PVI tiene una solución?
(b) ¿Para qué puntos (x₀, y₀) implica el teorema 9.2.3.1 (b) que este PVI tiene una solución única en algún intervalo abierto que contiene x₀?
Solución:
(a) Dado que


es continua para todo (x, y), el teorema 9.2.3.1 implica que el PVI dado tiene una solución para todo (x₀, y₀).
(b) Aquí
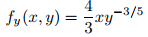
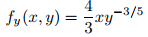
es continua para todo (x, y) con y ≠ 0. Por lo tanto, si y ≠ 0 hay un rectángulo abierto en el que tanto f como fy son continuas, y el teorema 9.2.3.1 implica que el PVI dado tiene un solución en algún intervalo abierto que contiene x₀. ♦
Si y = 0 entonces fy(x, y) es indefinido y, por lo tanto, discontinua; por tanto, el teorema 9.2.3.1 no se aplica a este PVI si y₀ = 0.
Ejemplo ilustrativo 9.2.3_6
El ejemplo anterior 9.2.3_5 deja abierta la posibilidad de que el problema del valor inicial
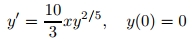
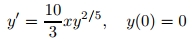
tiene más de una solución en cada intervalo abierto que contiene x₀ = 0. Demuestre que esto es cierto.
Solución:
Por inspección, y ≡ 0 es una solución de la ecuación diferencial


Dado que y ≡ 0 satisface la condición inicial y(0) = 0, es una solución del PVI dado.
Ahora suponga que y es una solución de la ecuación diferencial que no es idénticamente cero. Al separar variables en la ED, se obtiene


en cualquier intervalo abierto donde y no tenga ceros. Integrar esto y reescribir la constante arbitraria como 5c/3 produce


Por lo tanto


Dado que dividimos por y para separar variables en la ED, nuestra deducción de esta solución general es legítima sólo en intervalos abiertos donde y no tiene ceros. Sin embargo, la solución general deducida realmente define y para todo x, y la diferenciación de esta solución general muestra que


Por lo tanto esta solución general satisface la ED en (−∞, ∞) incluso si c ≤ 0, de modo que y(√|c|) = y(−√|c|) = 0. En particular, tomando c = 0 en la solución general, obtenemos


como una segunda solución del PVI. Ambas soluciones se definen en (−∞, ∞) y difieren en cada intervalo abierto que contiene x₀ = 0 (consulte la figura 9.2.3_2.) De hecho, hay cuatro soluciones distintas del PVI dado definidas en (−∞, ∞) que difieren entre sí en cada intervalo abierto que contiene x₀ = 0. ¿Puedes identificar las otros dos? ♦


Figura 9.2.3_2 Dos soluciones (y = 0 e y = x^10/3) del PVI dado que difieren en cada intervalo que contiene x₀ = 0
Ejemplo ilustrativo 9.2.3_7
Del ejemplo 9.2.3_5, el problema de valor inicial
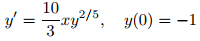
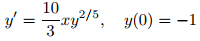
tiene una solución única en algún intervalo abierto que contiene x₀ = 0. Encuentre una solución y determine el intervalo abierto más grande (a, b) en el que es única.
Solución:
Sea y cualquier solución del presente PVI. Debido a la condición inicial y(0) = −1 y la continuidad de y, hay un intervalo abierto I que contiene x₀ = 0 en el que y no tiene ceros y, en consecuencia, tiene la forma (9.2.3.11). Establecer x = 0 e y = −1 en (9.2.3.11) produce c = −1, entonces
y = (x2 − 1)5/3 (9.2.3.13)
para x en I. Por lo tanto, toda solución del presente PVI difiere de cero y está dada por (9.2.3.13) en (−1, 1); es decir, (9.2.3.13) es la única solución del PVI en (−1, 1). Este es el intervalo abierto más grande en el que el PVI tiene una solución única. Para ver esto, observe que (9.2.3.13) es una solución del presente PVI en (−∞, ∞).
Hay infinitas otras soluciones del presente PVI que difieren de (9.2.3.13) en cada intervalo abierto mayor que (−1, 1). Una de esas soluciones es (observe la figura 9.2.3_3). ♦


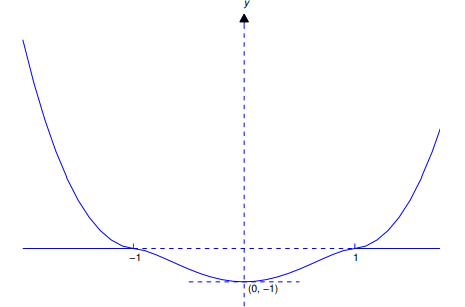

Figura 9.2.3_3 Dos soluciones del PVI del ejemplo ilustrativo 9.2.3_7 en (−∞, ∞) que coinciden en (−1, 1), pero no en un intervalo abierto mayor.
Ejemplo ilustrativo 9.2.3_8
Del ejemplo 9.2.3_5, el problema de valor inicial
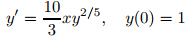
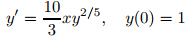
tiene una solución única en algún intervalo abierto que contiene x₀ = 0. Encuentre la solución y determine el intervalo abierto más grande en el que es única.
Solución:
Sea y cualquier solución de este PVI. Debido a la condición inicial y(0) = 1 y la continuidad de y, hay un intervalo abierto I que contiene x₀ = 0 en el que y no tiene ceros y, en consecuencia, tiene la forma





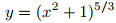
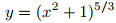
para x en I. Por lo tanto, toda solución del presente PVI difiere de cero y está dada por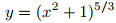
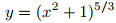
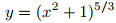
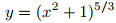


Figura 9.2.3_4 La única solución del PVI del ejemplo ilustrativo 9.2.3_8.
