| 1. Funciones y sus gráficas |
1.2. Clases básicas de funciones: Objetivos de aprendizaje
1.2.1. Calcular la pendiente de una función lineal e interpretar su significado.
1.2.2. Reconocer el grado de un polinomio.
1.2.3. Encontrar las raíces de un polinomio cuadrático.
1.2.4. Describir las gráficas de funciones polinómicas básicas pares e impares.
1.2.5. Identificar una función racional.
1.2.6. Describir las gráficas funciones de potencia y raíz.
1.2.7. Explicar la diferencia entre las funciones algebraicas y trascendentales.
1.2.8. Graficar una función definida por tramos.
1.2.9. Dibujar la gráfica de una función que se ha desplazado, estirado o reflejado desde su gráfica en la posición inicial.
| Ejercicios propuestos del Capítulo 1.2 | Ejercicios resueltos del Capítulo 1.2 |
Hemos estudiado las características generales de las funciones, así que ahora examinemos algunas clases específicas de funciones. Comenzamos revisando las propiedades básicas de las funciones lineales y cuadráticas, y luego generalizamos para incluir polinomios de mayor grado. Al combinar funciones de raíz con polinomios, podemos definir funciones algebraicas generales y distinguirlas de las funciones trascendentales que examinaremos más adelante en este capítulo. Terminamos la sección con ejemplos de funciones definidas por tramos y veremos cómo dibujar la gráfica de una función que se ha desplazado, estirado o reflejado desde su forma inicial.
Funciones lineales y la pendiente de una recta
El tipo de función más fácil de considerar es una función lineal. Las funciones lineales tienen la forma f (x) = ax + b, donde a y b son constantes. En la figura 1.2.1, vemos ejemplos de funciones lineales cuando a es positivo, negativo y cero. Tenga en cuenta que si a > 0, la gráfica de la recta crece a medida que x aumenta, en otras palabras, f (x) = ax + b crece en (−∞, ∞). Si a < 0, la gráfica de la recta decrece a medida que x aumenta. En este caso, f (x) = ax + b está decreciendo en (−∞, ∞). Si a = 0, la recta es horizontal
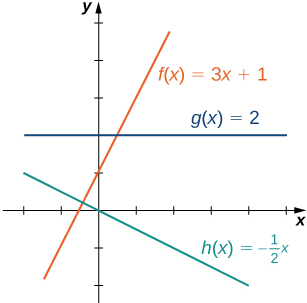
Pendiente de una recta
Como sugiere la figura 1.2.1, la gráfica de cualquier función lineal es una recta. Una de las características distintivas de una recta es su pendiente. La pendiente es el cambio en y para cada cambio de unidad en x. La pendiente mide tanto la inclinación como la dirección de una recta. Si la pendiente es positiva, la recta apunta hacia arriba cuando se mueve de izquierda a derecha. Si la pendiente es negativa, la recta apunta hacia abajo cuando se mueve de izquierda a derecha. Si la pendiente es cero, la recta es horizontal. Para calcular la pendiente de una recta, necesitamos determinar la razón del cambio en y versus el cambio en x. Para hacerlo, elegimos dos puntos (x1, y1) y (x2, y2) en la recta y calculamos el cociente ( y2 − y1)/(x2 − x1). En la figura 1.2_2, vemos que esta relación es independiente de los puntos elegidos.
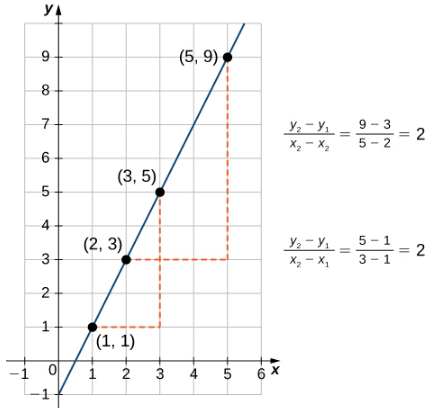

Definición 1.2_1. Pendiente de una recta
|
Considere la recta L que pasa por los puntos (x1, y1) y (x2, y2). Supongamos que Δy = y2 − y1 y Δx = x2 − x1 denotan los cambios en y y en x, respectivamente. La pendiente de la recta, m, es
|
Formas de la ecuación de la recta
Ahora examinamos la relación entre la pendiente y la fórmula para una función lineal. Considere la función lineal dada por la fórmula f (x) = ax + b. Como se discutió anteriormente, sabemos que la gráfica de una función lineal está dado por una recta. Podemos usar nuestra definición de pendiente para calcular la pendiente de esta recta. De acuerdo con la fórmula, podemos determinar la pendiente calculando (y2 − y1) / (x2 − x1) para cualquier punto (x1, y1) y (x2, y2) en la recta. Al evaluar la función f en x = 0, vemos que (0, b) es un punto en esta recta. Al evaluar esta función en x = 1, vemos que (1, a + b) también es un punto en esta recta. Por lo tanto, la pendiente de esta recta es


Hemos demostrado que el coeficiente a es la pendiente de la recta. Podemos concluir que la fórmula f (x) = ax + b describe una recta con pendiente a. Además, debido a que esta recta intersecta el eje y en el punto (0, b), vemos que la intersección y para esta función lineal es (0, b). Concluimos que la fórmula f (x) = ax + b nos muestra la pendiente, a, y el intercepto y, (0, b), para esta recta. Como a menudo usamos el símbolo m para denotar la pendiente de una recta, podemos escribir
f (x) = mx + b
para denotar la forma pendiente-intercepto de una función lineal.
A veces es conveniente expresar una función lineal de diferentes maneras. Por ejemplo, suponga que la gráfica de una función lineal pasa a través del punto (x1, y1) y la pendiente de la recta es m. Dado que cualquier otro punto (x, f (x)) en la gráfica de f debe satisfacer la ecuación


esta función lineal se puede expresar escribiendo
f (x) − y1 = m (x − x1).
Llamamos a esta ecuación la ecuación punto-pendiente para esa función lineal.
Dado que cada recta no vertical es la gráfica de una función lineal, los puntos en una recta no vertical se pueden describir utilizando las ecuaciones de la recta pendiente-intercepto o punto-pendiente. Sin embargo, una recta vertical no representa la gráfica de una función y no puede expresarse en ninguna de estas formas. En cambio, una recta vertical se describe mediante la ecuación x = k para alguna constante k. Dado que ni la forma pendiente-intercepto ni la forma punto-pendiente permiten rectas verticales, usamos la notación
ax + by = c,
donde a, b no son ambos cero, para denotar la forma estándar de una recta.
Definición 1.2_2. Ecuaciones de la recta
♦ Considere una recta que pasa por el punto (x1, y1) con pendiente m. La ecuación
y − y1 = m (x − x1)
es la ecuación punto-pendiente para esa recta.
♦ Considere una recta con pendiente m e intersección con y el punto (0, b). La ecuación
y = mx + b
es una ecuación para esa recta en forma pendiente-intersección (canónica).
♦ La forma estándar (general) de una recta viene dada por la ecuación
ax + by = c,
donde a y b no son ambos cero. Esta forma es más general porque permite una recta vertical, x = k.
EJEMPLO ILUSTRATIVO 1.2_1. Encontrar la pendiente y las ecuaciones de la recta
Considere la recta que pasa por los puntos (11, −4) y (−4, 5), como se muestra en la Figura 1.2_3.


a. Encuentra la pendiente de la recta.
b. Encuentre una ecuación para esta función lineal en forma punto-pendiente.
c. Encuentre una ecuación para esta función lineal en forma de pendiente-intersección.
Solución:
a. La pendiente de la recta es
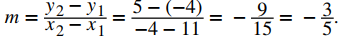
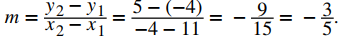
b. Para encontrar una ecuación para la función lineal en forma de punto-pendiente, use la pendiente m = −3 / 5 y elija cualquier punto de la recta. Si elegimos el punto (11, −4), obtenemos la ecuación
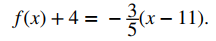
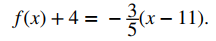
c. Para encontrar una ecuación para la función lineal en forma de pendiente-intersección, resuelva la ecuación en la parte b. para f (x). Cuando hacemos esto, obtenemos la ecuación
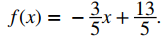
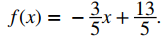
EJERCICIO DE CONTROL 1.2_1
Considere la recta que pasa por los puntos (−3, 2) y (1, 4).
- Encuentre la pendiente de la recta.
- Encuentre una ecuación de esa recta en forma de punto-pendiente.
- Encuentre una ecuación de esa recta en forma de pendiente-intersección.
EJEMPLO ILUSTRATIVO 1.2_2. Una función de distancia lineal
Jessica sale de su casa a las 5:50 a.m. y va a correr 9 millas. Ella regresa a su casa a las 7:08 a.m. Responde las siguientes preguntas, suponiendo que Jessica corre a un ritmo constante.
a. Describa la distancia D (en millas) que Jessica corre como una función lineal de su tiempo de ejecución t (en minutos).
b. Dibuja una gráfica de la función D.
c. Interpreta el significado de la pendiente.
Solución:
a. En el tiempo t = 0, Jessica está en su casa, entonces D(0) = 0. En el tiempo t = 78 minutos, Jessica ha terminado de correr 9 millas, entonces D(78) = 9. La pendiente de la función lineal es


La intersección en y es (0, 0), el origen de coordenadas, por lo que la ecuación para esta función lineal es
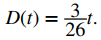
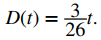
b. Para graficar D, use el hecho de que la gráfica pasa por el origen y tiene una pendiente m = 3/26.


c. La pendiente m = 3 / 26 ≈ 0.115 describe la distancia (en millas) que Jessica corre por minuto, o su velocidad promedio.


Cómo determinar la paridad de la función y=2x-6
Hola. La función y = f(x) = 2x – 6 no es par ni impar.
• Una función es par si f(–x) = f(x).
• Una función es impar si f(–x) = –f(x)