| 9. Ecuaciones diferenciales | 9.7.Soluciones en serie de ecuaciones lineales de segundo orden |

9.7.3 Soluciones en serie cerca de un punto ordinario II

      En esta sección seguimos encontrando soluciones en serie de potencias

de problemas de valor inicial

        (9.7.3.1)

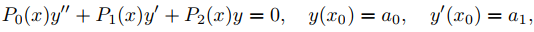
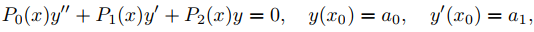
donde P₀, P₁ y P₂ son polinomios y P₀(x₀) ≠ 0, por lo que x₀ es un punto ordinario de (9.7.3.1). Sin embargo, aquí consideramos casos donde la ecuación diferencial en (9.7.3.1) no es de la forma

por lo tanto, el teorema 9.7.2.2 no se aplica y el cálculo de los coeficientes {a_n} es más complicado. Para las ecuaciones consideradas aquí es difícil o imposible obtener una fórmula explícita para a_n en términos de n. No obstante, podemos calcular tantos coeficientes como queramos. Los siguientes tres ejemplos ilustran esto.

Ejemplo 9.7.3.1

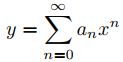
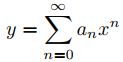
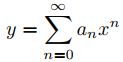
Encuentre los coeficientes a₀, . . . , a₇ en la solución en serie del problema de valor inicial

      (9.7.3.2)

Solución:
Aquí

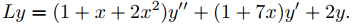
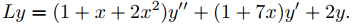
Los ceros (−1 ± i√7)/4 de P₀(x) = 1 + x + 2x² tienen valor absoluto 1/√2, por lo que el Teorema 9.7.2.2 implica que la solución en serie converge a la solución de (9.7.3.2 ) en (−1/√2, 1/√2). Ya que

   y   

Cambiando los índices para que el término general en cada serie sea un múltiplo constante de xⁿ se obtiene

donde

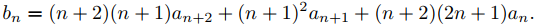
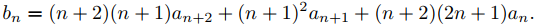
Por lo tanto es una solución de Ly = 0 si y solo si

        (9.7.3.3)   

De las condiciones iniciales en (9.7.3.2), a₀ = y(0) = −1 y a₁ = y′(0) = −2. Establecer n = 0 en (9.7.3.3) produce

Establecer n = 1 en (9.7.3.3) produce

Te dejamos a ti calcular a₄, a₅, a₆, a₇ de (9.7.3.3) y mostrar que

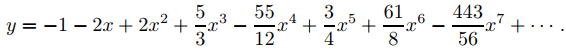
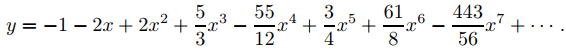
Te dejamos también (Ejercicio 13) comprobar numéricamente que los polinomios de Taylor convergen a la solución de (9.7.3.2) en (−1/√2, 1/√2). ♦

Ejemplo 9.7.3.2

Encuentre los coeficientes a₀, . . . , a₅ en la solución en serie

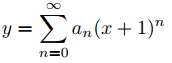
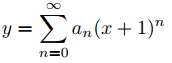
del problema de valor inicial

        (9.7.3.4)

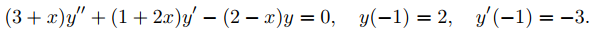
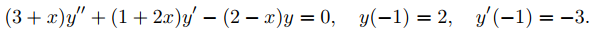
Solución:
Como la serie deseada está en potencias de x + 1, reescribimos la ecuación diferencial en (9.7.3.4) como Ly = 0, con

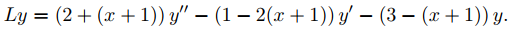
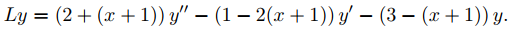
Ya que

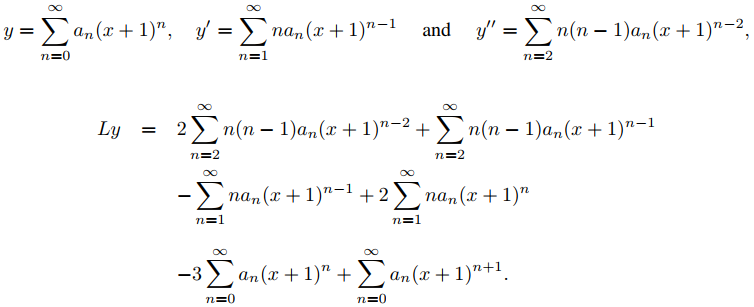
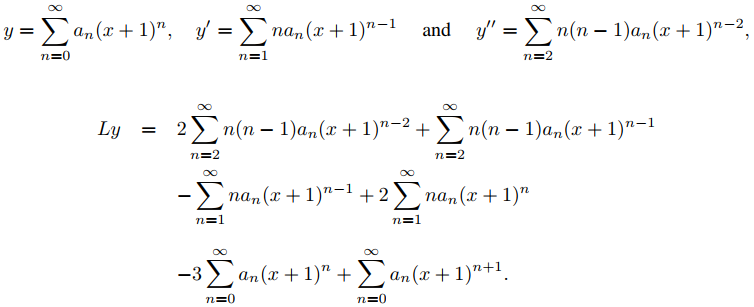
Cambiando los índices de manera que el término general en cada serie sea un múltiplo constante de (x + 1)ⁿ se obtiene

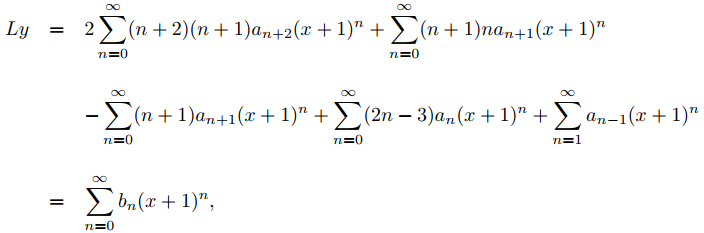
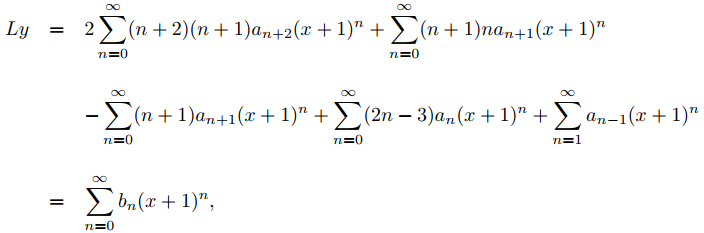
donde 

y

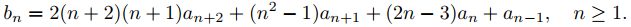
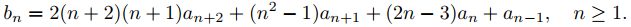
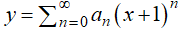
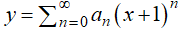
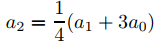
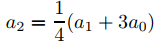
Por lo tanto es una solución de Ly = 0 si y sólo si

      (9.7.3.5)

y

        (9.7.3.6)

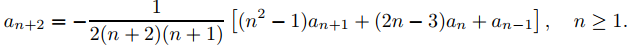
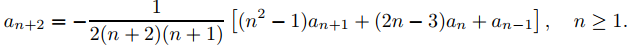
De las condiciones iniciales en (9.7.3.4), a₀ = y(−1) = 2 y a₁ = y′(−1) = −3. Te dejamos a ti calcular a₂, . . . , a₅ con (9.7.3.5) y (9.7.3.6) y demuestre que la solución de (9.7.3.4) es

Te dejamos también (Ejercicio 14) comprobar numéricamente que los polinomios de Taylor convergen a la solución de (9.7.3.4) en el intervalo de convergencia de la solución en serie de potencias.  ♦

Ejemplo 9.7.3.3

Encuentre los coeficientes a₀, . . . , a₅ en la solución en serie del problema de valor inicial

        (9.7.3.7)

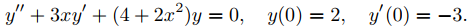
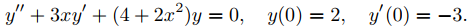
Solución:
Aquí

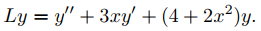
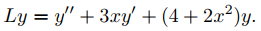
Ya que

    y   

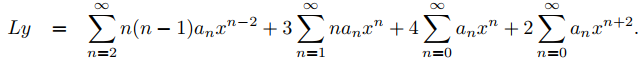
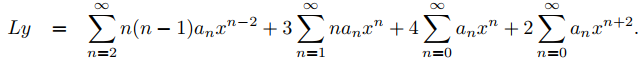
Cambiando los índices para que el término general en cada serie sea un múltiplo constante de xⁿ se obtiene

donde

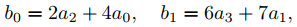
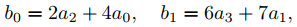
y

Por lo tanto es una solución de Ly = 0 si y sólo si

        (9.7.3.8)

y

        (9.7.3.9)

De las condiciones iniciales en (9.7.3.7), a₀ = y(0) = 2 y a₁ = y′(0) = −3. Te dejamos a ti calcular a₂, . . . , a₅ con (9.7.3.8) y (9.7.3.9) y demuestre que la solución de (9.7.3.7) es

Te dejamos también (Ejercicio 15) comprobar numéricamente que los polinomios de Taylor convergen a la solución de (9.7.3.9) en el intervalo de convergencia de la solución en serie de potencias.