| 9. Ecuaciones diferenciales |
9.12 Soluciones de Fourier de ecuaciones diferenciales parciales
EN ESTE CAPÍTULO usamos las series de Fourier discutidas en el Capítulo 11 para resolver ecuaciones diferenciales parciales que surgen en problemas de física matemática.
LA SECCIÓN 9.12.1 trata de la ecuación diferencial parcial
ut = a2uxx ,
que surge en problemas de conducción del calor.
LA SECCIÓN 9.12.2 trata de la ecuación diferencial parcial
utt = a2uxx ,
que surge en el problema de la cuerda vibrante.
LA SECCIÓN 9.12.3 trata de la ecuación diferencial parcial
uxx + uyy = 0,
que surge en problemas de estado estacionario de conducción de calor y teoría del potencial.
LA SECCIÓN 9.12.4 trata de la ecuación diferencial parcial
que es el equivalente a la ecuación estudiada en la Sección 9.12.3 cuando las variables independientes son coordenadas polares.
9.12.1 LA ECUACIÓN DEL CALOR
Comenzamos el estudio de las ecuaciones diferenciales parciales con el problema de flujo de calor en una barra uniforme de longitud L, situada en el eje x con un extremo en el origen y el otro en x = L (Figura 9.12.1.1).
Figura 9.12.1.1 Una barra uniforme de longitud L
Suponemos que la barra está perfectamente aislada, excepto posiblemente en sus extremos, y que la temperatura es constante en cada sección transversal y, por lo tanto, depende solo de x y t. También suponemos que las propiedades térmicas de la barra son independientes de x y t. En este caso, se puede demostrar que la temperatura u = u(x, t) en el tiempo t en un punto x unidades desde el origen satisface la ecuación diferencial parcial
ut = a2uxx , 0 < x < L, t > 0,
donde a es una constante positiva determinada por las propiedades térmicas. Esta es la ecuación del calor.
Para determinar u, debemos especificar la temperatura en cada punto de la barra cuando t = 0, digamos
u(x, 0) = f (x), 0 ≤ x ≤ L.
A esto lo llamamos la condición inicial. También debemos especificar las condiciones de contorno que u debe satisfacer en los extremos de la barra para todo t > 0. A este problema lo llamaremos problema de valores iniciales y de contorno.
Comenzamos con las condiciones de contorno u(0, t) = u(L, t) = 0, y escribimos el problema de valores iniciales y de contorno como
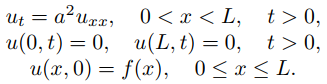(9.12.1.1)
Nuestro método para resolver este problema se llama separación de variables (que no debe confundirse con el método de separación de variables utilizado en la Sección 9.2.2 para resolver ecuaciones diferenciales ordinarias). Comenzamos buscando funciones de la forma
v(x, t) = X(x)T(t)
que no son idénticamente cero y satisfacen
vt = a2vxx y v(0, t) = 0, v(L, t) = 0
para todo (x, t). Teniendo presente que
vt = XT′ y vxx = X′′T,
vt = a2vxx si y solo si
XT′ = a2X′′T,
que podemos reescribir como
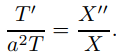
Dado que la expresión de la izquierda es independiente de x mientras que la de la derecha es independiente de t, esta ecuación se puede cumplir para todo (x, t) solo si los dos lados son iguales a la misma constante, que llamamos constante de separación, y escríbala como −λ; de este modo,
Esto es equivalente a
X′′ + λX = 0
y
T′ = −a2λT. (9.12.1.2)
Dado que v(0, t) = X(0)T(t) = 0 y v(L, t) = X(L)T(t) = 0 y no queremos que T sea idénticamente cero, X(0) = 0 y X(L) = 0. Por lo tanto, λ debe ser un valor propio del problema de valores en la frontera
X′′ + λX = 0, X(0) = 0, X(L) = 0, (9.12.1.3)
y X debe ser una función propia λ. Del Teorema 9.11.1.2, los valores propios de (9.12.1.3) son λn = n2π2/L2, con funciones propias asociadas
Sustituyendo λ = n2π2/L2 en (9.12.1.2) se obtiene
T′ = −(n2π2a2/L2)T,
que tiene la solución
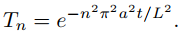
Ahora, sea
Ya que
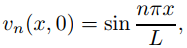
vn satisface (9.12.1.1) con f (x) = sennπx/L. Más generalmente, si α1, . . ., αm son constantes y
entonces um satisface (9.12.1.1) con
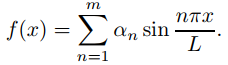
Esto motiva la siguiente definición.
Definición 9.12.1.1
La solución formal del problema de valor inicial y de frontera
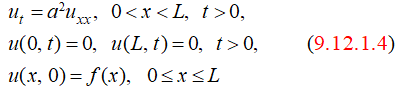
es
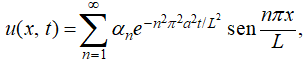(9.12.1.5)
donde
es la serie de senos de Fourier de f en [0, L]; es decir,
♦
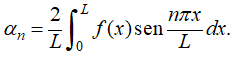
Usamos el término “solución formal” en esta definición porque, en general, no es cierto que la serie infinita en (9.12.1.5) en realidad satisfaga todos los requisitos del problema de valor inicial y de frontera (9.12.1.4) cuando lo hace, decimos que es una solución real de (9.12.1.4).
Debido a las exponenciales negativas en (9.12.1.5), u converge para todo (x, t) con t > 0 (Ejercicio 54). Dado que cada término en (9.12.1.5) satisface la ecuación del calor y las condiciones de contorno en (9.12.1.4), u también tiene estas propiedades si ut y uxx se pueden obtener derivando la serie en (9.12.1.5) término por término una vez con respecto a t y dos veces con respecto a x, para t > 0. Sin embargo, no siempre es legítimo diferenciar una serie infinita término por término. El siguiente teorema da una condición suficiente útil para la legitimidad de la diferenciación término por término de una serie infinita. Omitimos la demostración.
Teorema 9.12.1.1
Una serie infinita convergente
puede diferenciarse término a término en un intervalo cerrado [z1, z2] para obtener
(donde las derivadas en z = z1 y z = z2 son unilaterales) siempre que w′n sea continua en [z1, z2] y
|w′n(z)| ≤ MN, z1 ≤ z ≤ z2, n = 1, 2, 3, . . .,
donde M1, M2, . . . , Mn, . . . , son constantes tales que la serie 
converge. ♦
El teorema 9.12.1.1, aplicado dos veces con z = x y una vez con z = t, muestra que uxx y ut pueden obtenerse derivando u término por término si t > 0 (Ejercicio 54). Por lo tanto, u satisface la ecuación del calor y las condiciones de contorno en (9.12.1.4) para t > 0. Por lo tanto, dado que u(x, 0) = S(x) para 0 ≤ x ≤ L, u es una solución real de (9.12.1 .4) si y solo si S(x) = f (x) para 0 ≤ x ≤ L. Del Teorema 9.11.3.2, esto es cierto si f es continua y uniforme a trozos en [0, L], y f (0 ) = f (L) = 0.
En este capítulo definiremos soluciones formales de varios tipos de problemas. Cuando le pedimos que resuelva tales problemas, siempre queremos decir que debe encontrar una solución formal.
Ejemplo ilustrativo 9.12.1.1
Resuelve (9.12.1.4) con f (x) = x(x2 − 3Lx + 2L2).
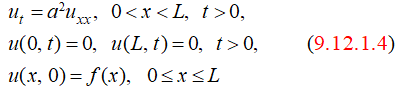
Solución:
Del Ejemplo 9.11.3.6, la serie de senos de Fourier de f en [0, L] es
Por lo tanto
♦
Si ambos extremos de la barra están aislados para que no pase calor a través de ellos, entonces las condiciones de contorno son
ux(0, t) = 0, ux(L, t) = 0, t > 0.
Te dejamos (Ejercicio 1) usar el método de separación de variables y el Teorema 9.11.1.3 para motivar la siguiente definición.
Definición 9.12.1.2
La solución formal del problema de valor inicial y de frontera
es
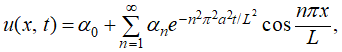
donde
es la serie de coseno de Fourier de f en [0, L]; es decir,
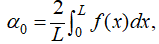y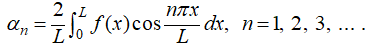 
♦
Ejemplo ilustrativo 9.12.1.2
Resuelva (9.12.1.6) con f (x) = x.
Solución:
Del Ejemplo 9.11.3.1, la serie de coseno de Fourier de f en [0, L] es
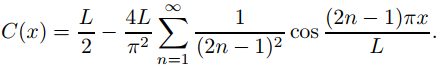
Por lo tanto
♦
Te dejamos (Ejercicio 2) usar el método de separación de variables y el Teorema 9.11.1.4 para motivar la siguiente definición.
Definición 9.12.1.3
La solución formal del problema de valor inicial y de frontera
es
donde
es la serie mixta de senos de Fourier de f en [0, L]; es decir,
♦
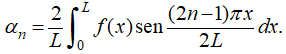Ejemplo ilustrativo 9.12.1.3
Resuelva (9.12.1.7) con f (x) = x.
Solución:
Del Ejemplo 9.11.3.4, la serie mixta de senos de Fourier de f en [0, L] es
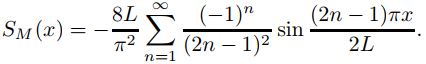
Por lo tanto
♦
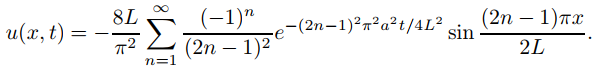La figura 9.12.1.2 muestra una gráfica de u = u(x, t) trazada con respecto a x para varios valores de t. La recta y = x corresponde a t = 0. Las otras curvas corresponden a valores positivos de t. A medida que t aumenta, las gráficas se aproximan a la recta u = 0.
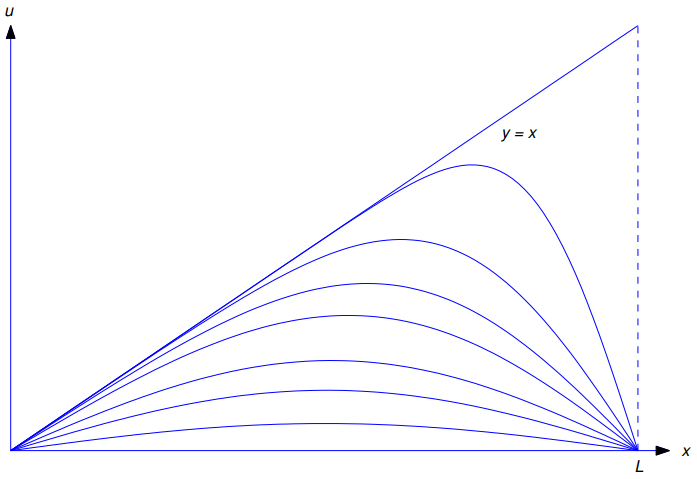
Figura 9.12.1.2
Te dejamos (Ejercicio 3) usar el método de separación de variables y el Teorema 9.11.1.5 para motivar la siguiente definición.
Definición 9.12.1.4
La solución formal del problema de valor inicial y de frontera
es
donde
es la serie mixta de cosenos de Fourier de f en [0, L]; es decir,
♦
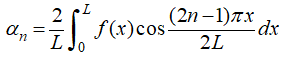Ejemplo ilustrativo 9.12.1.4
Resuelva (9.12.1.8) con f (x) = x − L.
Solución:
Del Ejemplo 9.11.3.3, la serie mixta de cosenos de Fourier de f en [0, L] es
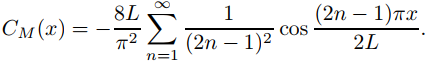
Por lo tanto
♦
Problemas no homogéneos
Un problema de la forma
(9.12.1.9)
puede transformarse en un problema que puede resolverse mediante la separación de variables. Escribimos
u(x, t) = v(x, t) + q(x), (9.12.1.10)
donde se va a determinar q. Entonces
ut = vt y uxx = vxx + q′′
entonces u satisface (9.12.1.9) si v satisface
Esto se reduce a
(9.12.1.11)
si
a2q′′ + h(x) = 0, q(0) = u0, q(L) = uL.
Podemos obtener q integrando q′′ = −h/a2 dos veces y eligiendo las constantes de integración para que q(0) = u0 y q(L) = uL. Entonces podemos resolver (9.12.1.11) para v por separación de variables, y (9.12.1.10) es la solución de (9.12.1.9).
Ejemplo ilustrativo 9.12.1.5
Resolver
Solución:
Le dejamos a usted mostrar que
q(x) = x2 + x − 1
satisface
q′′ − 2 = 0, q(0) = −1, q(1) = 1.
Por lo tanto
u(x, t) = v(x, t) + x2 + x − 1,
donde
y
v(x, 0) = x3 − 2x2 + 3x − 1 − x2 − x + 1 = x(x2 − 3x + 2).
Del Ejemplo 9.12.1.1 con a = 1 y L = 1,
Por lo tanto
♦
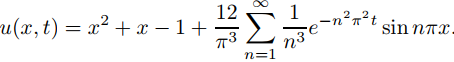Un procedimiento similar funciona si las condiciones de contorno en (9.12.1.11) se reemplazan por condiciones de contorno mixtas
ux(0, t) = u0, u(L, t) = uL, t > 0
o
u(0, t) = u0, ux(L, t) = uL, t > 0;
sin embargo, esto no es cierto en general para las condiciones de contorno
ux(0, t) = u0, ux(L, t) = uL, t > 0;
(Consulte el Ejercicio 92.1.47).
USO DE TECNOLOGÍA
Los experimentos numéricos pueden mejorar su comprensión de las soluciones de los problemas de valor inicial y de frontera. Para ser específicos, considere la solución formal
de (9.12.1.4), donde
es la serie de senos de Fourier de f en [0, L]. Considere la m-ésima suma parcial
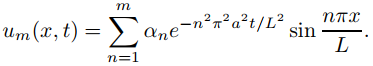(9.12.1.12)
Para varios valores fijos de t (incluido t = 0), grafique um(x, t) frente a t. En algunos casos, puede ser útil graficar las curvas correspondientes a los diversos valores de t en los mismos ejes; en otros casos, es posible que desee graficar las diversas curvas sucesivamente (para aumentar los valores de t) y crear una película primitiva en su monitor. Repita este experimento para varios valores de m, para comparar cómo los resultados dependen de m para valores pequeños y grandes de t. Sin embargo, tenga en cuenta que los significados de “pequeño” y “grande” en este caso dependen de las constantes a2 y L2. Una buena manera de manejar esto es reescribir (9.12.1.12) como
donde
(9.12.1.13)
y grafique um versus x para valores seleccionados de τ.
Estos comentarios también se aplican a las situaciones consideradas en las Definiciones 9.12.1.2 a 9.12.1.4, excepto que (9.12.1.13) debe reemplazarse por
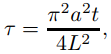
en las Definiciones 9.12.1.3 y 9.12.1.4.
En algunos de los ejercicios decimos “realizar experimentos numéricos”. Esto significa que debe realizar los cálculos recién descritos con la solución formal obtenida en el ejercicio.