| 2. Límites y continuidad |
2.3 LAS LEYES DE LÍMITES: Objetivos de aprendizaje
2.3.1. Reconocer las leyes básicas de límite.
2.3.2. Usar las leyes de límites para evaluar el límite de una función.
2.3.3. Evaluar el límite de una función factorizando.
2.3.4. Usar las leyes de límites para evaluar el límite de una función polinómica o racional.
2.3.5. Evaluar el límite de una función factorizando o usando conjugados.
2.3.6. Evaluar el límite de una función utilizando el teorema de compresión.
En la sección anterior, evaluamos los límites observando gráficas o construyendo una tabla de valores. En esta sección, establecemos leyes para calcular límites y aprendemos cómo aplicar estas leyes. En el Proyecto del estudiante al final de esta sección, tiene la oportunidad de aplicar estas leyes límite para derivar la fórmula para el área de un círculo mediante la adaptación de un método ideado por el matemático griego Arquímedes. Comenzamos reexpresando dos resultados límite útiles de la sección anterior. Estos dos resultados, junto con las leyes de límites, sirven como base para calcular muchos límites.
Evaluación de límites aplicando las propiedades de límites
Las dos primeras leyes de límites se establecieron en “Dos límites importantes” de la sección anterior y las repetimos aquí. Estos resultados básicos, junto con las otras leyes de límites, nos permiten evaluar los límites de muchas funciones algebraicas.
TEOREMA 2.3.1 Resultados básicos de límites
|
Para cualquier número real a y cualquier constante c,
|
EJEMPLO ILUSTRATIVO 2.3_1. Evaluación de un límite básico
Evalúe cada uno de los siguientes límites utilizando El Teorema 2.3.1 “Resultados básicos de límites”.


Solución:
a. El límite de x cuando x se aproxima a a a es a: limx → 2x = 2.
b. El límite de una constante es esa constante: limx → 25 = 5.
Ahora echamos un vistazo a las leyes de límites, las propiedades individuales de los límites. Las pruebas que tienen estas leyes se omiten aquí.
TEOREMA 2.3.2 Leyes de límites
|
Sean f (x) y g (x) funciones definidas para todo x ≠ a en algún intervalo abierto que contenga a a. Suponga que L y M son números reales tales que limx → a f (x) = L y limx → a g (x) = M. Sea c una constante. Entonces, cada una de las siguientes afirmaciones es válida:
|
Ahora practicamos la aplicación de estas leyes de límites para evaluar un límite.
EJEMPLO ILUSTRATIVO 2.3_2. Evaluación de un límite utilizando las leyes de límites
Use las leyes de límites para evaluar limx → −3 (4x + 2).
Solución:
Apliquemos las leyes de límites paso a paso para asegurarnos de que entendemos cómo funcionan. Debemos tener en cuenta el requisito de que, en cada aplicación de una ley de límites, los nuevos límites deben existir para que sea posible aplicar la ley de límites correspondiente.
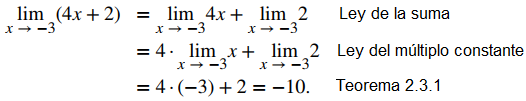
EJEMPLO ILUSTRATIVO 2.3_3. Uso de las leyes de límites repetidamente
Use las leyes de límites para evaluar
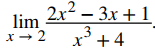
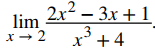
Solución:
Para encontrar este límite, necesitamos aplicar las leyes de límites varias veces. Nuevamente, debemos tener en cuenta que a medida que reescribimos el límite en términos de otros límites, cada nuevo límite debe existir para que se aplique la ley de límites.
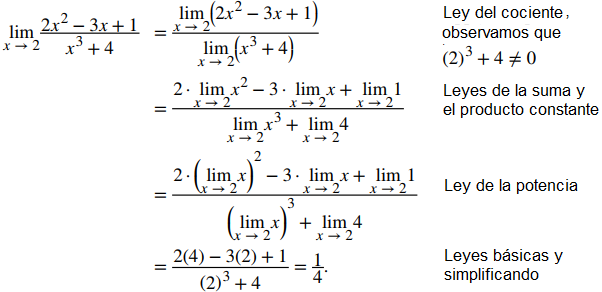
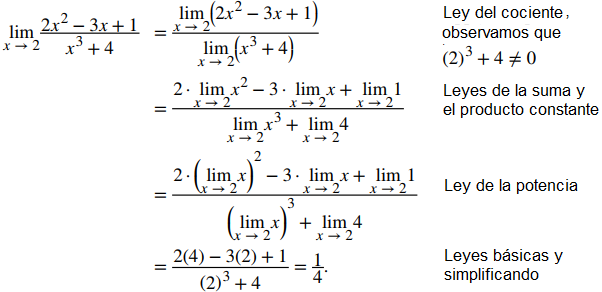
Ejercicio de control 2.3_1
Utilice las leyes de los límites para evaluar límx → 6 (2x − 1)√(x + 4). En cada paso, indique la ley límite aplicada.
Límites de funciones polinomiales y racionales
A estas alturas probablemente haya notado que, en cada uno de los ejemplos anteriores, ha sido el caso que
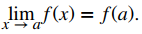
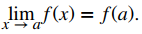
Esto no siempre es cierto, pero es válido para todos los polinomios para cualquier elección de a y para todas las funciones racionales en todos los valores de a para los que se define la función racional.
TEOREMA 2.3.3
Límites de funciones polinomiales y racionales
|
Supongamos que p(x) y q(x) son funciones polinómicas. Y sea a un número real. Entonces,
|
Para ver que este teorema es válido, considere el polinomio


Al aplicar las leyes de suma, múltiplo constante y potencia, terminamos con
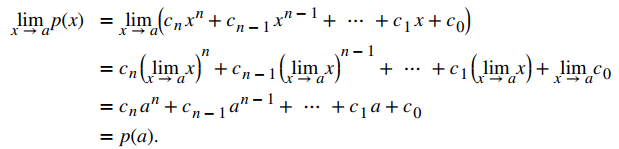
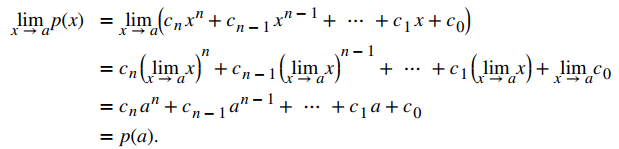
Ahora se deduce de la ley del cociente que si p(x) y q(x) son polinomios para los cuales q(a) ≠ 0, entonces
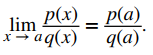
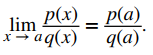
El ejemplo 2.3_4 aplica este resultado.
EJEMPLO ILUSTRATIVO 2.3_4. Evaluación de un límite de una función racional
Evalúa el siguiente límite
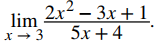
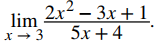
Dado que 3 está en el dominio de la función racional
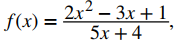
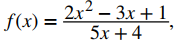
podemos calcular el límite sustituyendo 3 por x en la función. Así,
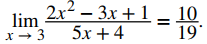
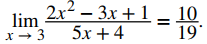
Ejercicio de control 2.3_2
Evalúe limx → −2 (3x3 − 2x + 7).
Técnicas adicionales de evaluación de límites
Como hemos visto, podemos evaluar fácilmente los límites de polinomios y los límites de algunas (pero no todas) funciones racionales por sustitución directa. Sin embargo, como vimos en la sección introductoria sobre límites, es ciertamente posible que limx → a f (x) exista cuando f (a) no está definido. La siguiente observación nos permite evaluar muchos límites de este tipo:
Si para todo x ≠ a, f (x) = g (x) en algún intervalo abierto que contenga a a, entonces
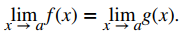
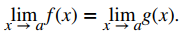
Para comprender mejor esta idea, considere el límite
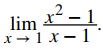
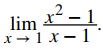
La función
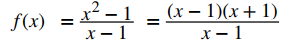
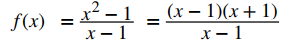
y la función g(x) = x + 1 son idénticas para todos los valores de x ≠ 1. Las gráficas de estas dos funciones se muestran en la Figura 2.3_1.
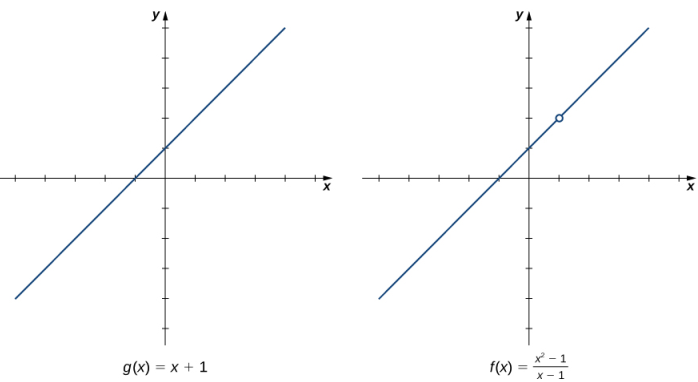

Podemos ver que
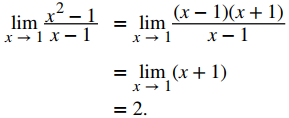
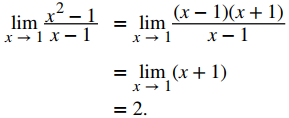
Los límites de la forma
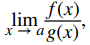
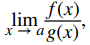
donde limx → a f (x) = 0 y limx → a g(x) = 0. (En este caso, decimos que f (x) / g(x) tiene la forma indeterminada 0/0.) La siguiente estrategia de resolución de problemas proporciona un esquema general para evaluar límites de este tipo.
Estrategia de resolución de problemas: Cálculo de un límite cuando f(x)/g(x) tiene la forma indeterminada 0/01. Primero, debemos asegurarnos de que nuestra función tenga la forma adecuada (0/0) y no pueda evaluarse de inmediato utilizando las leyes de límites. |
Los siguientes ejemplos demuestran el uso de esta estrategia de resolución de problemas. El ejemplo 2.3_5 ilustra la técnica de factorizar y cancelar; el ejemplo 2.3_6 muestra la multiplicación por un conjugado. En el ejemplo 2.3_7, observamos la simplificación de una fracción compleja.
EJEMPLO ILUSTRATIVO 2.3_5. Evaluación de un límite factorizando y cancelando
Evaluar


Solución:
Paso 1. La función


no está definido para x = 3. De hecho, si sustituimos 3 en la función obtenemos la forma indeterminada 0/0, que no está definido. Factorizar y cancelar es una buena estrategia:


Paso 2. Para todos los x ≠ 3,


Por lo tanto,
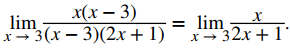
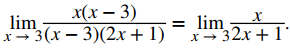
Paso 3. Evalúe usando las leyes de límites:


Ejercicio de control 2.3_3
Evalúe limx → −3 (x2 + 4x + 3) / (x2 − 9).
EJEMPLO ILUSTRATIVO 2.3_6. Evaluación de un límite multiplicando por un conjugado
Evaluar


Solución:
Paso 1. El cociente


tiene la forma 0/0 en −1. Comencemos multiplicando por √ (x + 2) + 1, el conjugado de √(x + 2) − 1, en el numerador y el denominador:
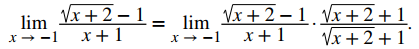
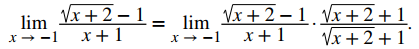
Paso 2. Luego multiplicamos el numerador. No multiplicamos el denominador porque esperamos que el factor (x + 1) en el denominador se cancele al final:


Paso 3. Luego cancelamos:
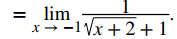
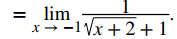
Paso 4. Por último, aplicamos las leyes de límites:


Ejercicio de control 2.3_4
Evalúe limx → 5(√(x − 1) − 2)/(x − 5).
EJEMPLO ILUSTRATIVO 2.3_7. Evaluación de un límite simplificando una fracción compleja
Evaluar



Solución:
Paso 1. La fracción compleja



tiene la forma 0/0 en 1. Simplificamos la fracción algebraica multiplicando por 2 (x + 1) / 2 (x + 1):


Paso 2. A continuación, multiplicamos por los numeradores. No multiplique los denominadores porque queremos poder cancelar el factor (x − 1):


Paso 3. Luego, simplificamos el numerador:
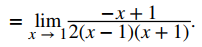
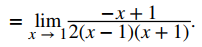
Paso 4. Ahora factorizamos el numerador por −1:


Paso 5. Luego, cancelamos los factores comunes de (x − 1):


Paso 6. Por último, evaluamos aplicando las leyes de límites:
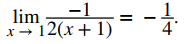
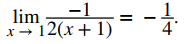
Ejercicio de control 2.3_5


El ejemplo 2.3._8 no encaja perfectamente en ninguno de los patrones establecidos en los ejemplos anteriores. Sin embargo, con un poco de creatividad, aún podemos usar estas mismas técnicas.
EJEMPLO ILUSTRATIVO 2.3_8. Evaluación de un límite cuando las leyes de límite no se aplican inmediatamente
Evaluar


Solución:
Tanto 1 / x como 5 / x (x − 5) no tienen un límite en cero. Como ninguna de las dos funciones tiene un límite en cero, no podemos aplicar la ley de suma para los límites; Debemos usar una estrategia diferente. En este caso, encontramos el límite realizando la suma y luego aplicando una de nuestras estrategias anteriores. Veamos


Así,


Ejercicio de control 2.3_6


Ejercicios resueltos
En los siguientes ejercicios, use la sustitución directa para mostrar que el límite conduce a la forma indeterminada 0/0. Luego, evalúe el límite:
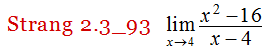
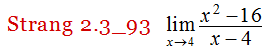
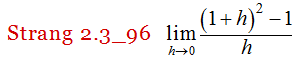
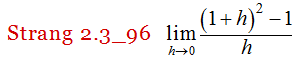


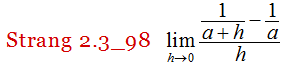
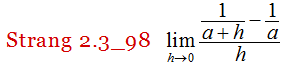


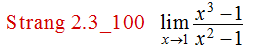
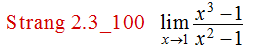


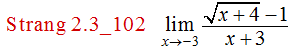
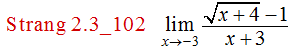

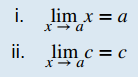

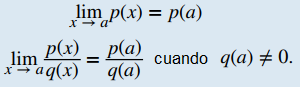
Excelente material. Muchas gracias.
Con mucho gusto 😺👍
Buenas tardes
Muy buen aporte.
Les envío un comentario sobre “CÁLCULO 21”
2.3 LAS LEYES DE LÍMITES: Objetivos de aprendizaje
TEOREMA 2.3.2 Leyes de límites
Raiz:
Donde dice:
“para todo L si n es par
y para L>=0 si n es impar”
Debería decir:
“Para todo L si n es impar.
Para todo L>=0 si n es par.”
Muchas gracias
Hola Hugo
Gracias por el comentario.
Tiene toda la razón! Ya lo he corregido 👍
Era muy difícil darme cuenta de ese error! 😺👍