| 9. Ecuaciones diferenciales | 9.5 Ecuaciones lineales de segundo orden |

9.5.2  Ecuaciones lineales homogéneas con coeficientes constantes

Si a, b y c son constantes reales y a ≠ 0, entonces

ay″ + by′ + cy = F(x)

se dice que es una ecuación lineal con coeficientes constantes. En esta sección consideramos la ecuación lineal con coeficientes constantes homogénea

ay″ + by′ + cy = 0        (9.5.2.1)

Como veremos, todas las soluciones de (9.5.2.1) están definidas en (−∞, ∞). Siendo así, omitiremos las referencias al intervalo sobre el que se definen las soluciones, o el intervalo sobre el que un conjunto dado de soluciones es un conjunto fundamental, etc., ya que el intervalo siempre será (−∞, ∞).

      La clave para resolver (9.5.2.1) es que si y = e^rx donde r es una constante, entonces el lado izquierdo de (9.5.2.1) es un múltiplo de e^rx; de tal modo que si y = e^rx entonces y′ = re^rx  y  y″ = r²e^rx, así que

ay″ + by′ + cy = ar²e^rx + bre^rx + ce^rx = (ar² + br + c)e^rx.        (9.5.2.2)

El polinomio cuadrático

p(r) = ar² + br + c

es el polinomio característico de (9.5.2.1), y p(r) = 0 es la ecuación característica. De (9.5.2.2) podemos ver que y = e^rx es una solución de (9.5.2.1) si y solo si p(r) = 0.

      Las raíces de la ecuación característica vienen dadas por la fórmula cuadrática

      (9.5.2.3)

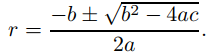
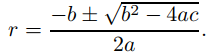
Consideramos tres casos:

CASO 1.  b² − 4ac > 0, por lo que la ecuación característica tiene dos raíces reales distintas.
CASO 2.  b² − 4ac = 0, por lo que la ecuación característica tiene dos raíces reales repetidas.
CASO 3.  b² − 4ac < 0, por lo que la ecuación característica tiene raíces complejas conjugadas.

En el estudio de cada caso, comenzaremos con un ejemplo.

Caso 1: Raíces Reales Distintas

Ejemplo ilustrativo 9.5.2_1

(a) Encuentre la solución general de

y″ + 6y′ + 5y = 0.        (9.5.2.4)

(b) Resuelva el problema de valor inicial

y″ + 6y′ + 5y = 0,   y(0) = 3, y′(0) = −1.        (9.5.2.5)

Solución:

(a) El polinomio característico de (9.5.2.4) es

p(r) = r² + 6r + 5 = (r + 1)(r + 5).

Como p(−1) = p(−5) = 0,  y₁ = e^−x  y  y₂ = e^−5x son soluciones de (9.5.2.4). Como y₂/y₁ = e^−4x no es constante, el Teorema 9.5.1.6 implica que la solución general de (9.5.2.4) es

y = c₁e^−x + c₂e^−5x.        (9.5.2.6)

(b) Debemos determinar c₁ y c₂ en (9.5.2.6) para que y satisfaga las condiciones iniciales en (9.5.2.5). Diferenciando (9.5.2.6), obtenemos

y′ = −c₁e^−x − 5c₂e^−5x.        (9.5.2.7)

Imponiendo las condiciones iniciales y(0) = 3, y′(0) = −1 en (9.5.2.6) y (9.5.2.7), se obtiene

La solución de este sistema es c₁ = 7/2, c₂ = −1/2. Por lo tanto la solución del PVI (9.5.2.5) es

La Figura 9.5.2.1 es un gráfico de esta solución.

(Figure 9.5.2.1)

      Si la ecuación característica tiene raíces reales distintas arbitrarias r₁  y  r₂, entonces y₁ = e^r₁x  y  y₂ = e^r₂x son soluciones de ay″ + by′ + cy = 0. Como y₂/y₁ = e^{(r₂ − r₁)x} no es constante, el Teorema 9.5.1.6 implica que {y₁, y₂} es un conjunto fundamental de soluciones de ay″ + by′ + cy = 0.

Caso 2: Raíces Reales Repetidas

Ejemplo ilustrativo 9.5.2_2

(a) Halle la solución general de 

y″ + 6y′ + 9y = 0.        (9.5.2.8)

(b) Resolver el problema de valor inicial

y″ + 6y′ + 9y = 0,  y(0) = 3,  y′(0) = −1.       (9.5.2.9)

Solución:

(a) El polinomio característico de (9.5.2.8) es

p(r) = r² + 6r + 9 = (r + 3)²,

por lo que la ecuación característica tiene la raíz real repetida r₁ = −3. Por lo tanto y₁ = e^−3x es una solución de (9.5.2.8). Como la ecuación característica no tiene otras raíces, (9.5.2.8) no tiene otras soluciones de la forma e^rx. Buscamos soluciones de la forma y = uy₁ = ue^−3x, donde u es una función que ahora determinaremos. (Esto debería recordarle el método de variación de parámetros utilizado en la Sección 9.2.1 para resolver la ecuación no homogénea y′ + p(x)y = f(x), dada una solución y₁ de la ecuación complementaria y′ + p(x)y = 0. También es un caso especial de un método llamado reducción de orden que estudiaremos en la Sección 9.5.6. Para conocer otras formas de obtener una segunda solución de (9.5.2.8) que no sea un múltiplo de e^−3x, consulte los Ejercicios 9.5.1.9, 9.5.1.12 y 33.

Si y = ue^−3x, entonces

y′ = u′e^−3x − 3ue^−3x  y  y″ = u″e^−3x − 6u′e^−3x + 9ue^−3x,

así que

Por lo tanto, y = ue^−3x es una solución de (9.5.2.8) si y solo si u″ = 0, lo que equivale a u = c₁ + c₂x, donde c₁ y c₂ son constantes. Por lo tanto, cualquier función de la forma

y = e^−3x(c₁ + c₂x)        (9.5.2.10)

es una solución de (9.5.2.8). Haciendo c₁ = 1 y c₂ = 0 se obtiene la solución y₁ = e^−3x que ya conocíamos. Haciendo c₁ = 0 y c₂ = 1 se obtiene la segunda solución y₂ = xe^−3x. Como y₂/y₁ = x no es constante, 9.5.1.6 implica que {y₁, y₂} es un conjunto fundamental de soluciones de (9.5.2.8), y (9.5.2.10) es la solución general.

(b) Derivando (9.5.2.10), se obtiene

y′ = −3e^−3x(c₁ + c₂x) + c₂e^−3x.        (9.5.2.11)

Imponiendo las condiciones iniciales y(0) = 3,  y′(0) = −1 en (9.5.2.10) y (9.5.2.11) se obtiene c₁ = 3  y  −3c₁ + c₂ = −1, por lo que c₂ = 8. Por lo tanto, la la solución de (9.5.2.9) es

y = e^−3x(3 + 8x)

La figura 9.5.2.2 es una gráfica de esta solución.

      Si la ecuación característica de ay″ + by′ + cy = 0 tiene una raíz real repetida r₁ arbitraria, el polinomio característico debe ser

p(r) = a(r − r₁)² = a(r² − 2r₁r + r₁²).

Por lo tanto

ar² + br + c = ar² − (2ar₁)r + ar₁²

lo que implica que b = −2ar₁  y  c = ar₁². Por lo tanto ay″ + by′ + cy = 0 se puede escribir como a(y″ − 2r₁y′ + r₁²y) = 0. Dado que a ≠ 0 esta ecuación tiene las mismas soluciones que

y″ − 2r₁y′ + r₁²y = 0.        (9.5.2.12)

      Como p(r₁) = 0,  y₁ = e^r₁x es una solución de ay″ + by′ + cy = 0, y por tanto de (9.5.2.12). Procediendo como en el Ejemplo 9.5.2.2, buscamos otras soluciones de (9.5.2.12) de la forma y = ue^r₁x; entonces

y′= u′e^r₁x + rue^r₁x    y    y″ = u″e^r₁x + 2r₁u′e^r₁x + r₁²ue^r₁x,

así que

Por lo tanto y = ue^r₁x es una solución de (9.5.2.12) si y solo si u″ = 0, lo que equivale a u = c₁ + c₂x, donde c₁ y c₂ son constantes. Por lo tanto, cualquier función de la forma

y = e^r₁x(c₁ + c₂x)        (9.5.2.13)

es una solución de (9.5.2.12). Haciendo c₁ = 1 y c₂ = 0 aquí se obtiene la solución y₁ = e^r₁x que ya conocíamos. Haciendo c₁ = 0 y c₂ = 1 se obtiene la segunda solución y₂ = xe^r₁x. Como y₂/y₁ = x no es constante, el Teorema 9.5.1.6 implica que {y₁, y₂} es un conjunto fundamental de soluciones de (9.5.2.12), y (9.5.2.13) es la solución general.

Caso 3: Raíces complejas conjugadas

Ejemplo ilustrativo 9.5.2_3

(a) Halle la solución general de 

y″ + 4y′ + 13y = 0.        (9.5.2.14)

(b) Resuelva el problema de valor inicial

y″ + 4y′ + 13y = 0,   y(0) = 2, y′(0) = −3.        (9.5.2.15)

Solución:

(a) El polinomio característico de (9.5.2.14) es

p(r) = r² + 4r + 13 = r² + 4r + 4 + 9 = (r + 2)² + 9.

Las raíces de la ecuación característica son r₁ = −2 + 3i  y  r₂ = −2 − 3i. Por analogía con el Caso 1, es razonable esperar que e^{(−2 + 3i)x}  y  e^{(−2 − 3i)x} sean soluciones de (9.5.2.14). Esto es cierto (ver Ejercicio 34); sin embargo, aquí hay dificultades, ya que probablemente no esté familiarizado con las funciones exponenciales con argumentos complejos, y aunque lo esté, es inconveniente trabajar con ellas, ya que son de valor complejo. Tomaremos un enfoque más simple, que motivamos de la siguiente manera: la notación exponencial sugiere que

e^{(−2 + 3i)x} = e^−2xe^3ix  y  e^{(−2 − 3i)x} = e^−2xe^−3ix, 

entonces, aunque no hemos definido e^3ix y e^−3ix, es razonable esperar que cada combinación lineal de e^{(−2 + 3i)x}  y  e^{(−2 − 3i)x} se pueda escribir como y = ue^−2x, donde u depende de x. Para determinar u, notamos que si y = ue^−2x entonces

y′ = u′e^−2x − 2ue^−2x  y  y″ = u″e^−2x − 4u′e^−2x + 4ue^−2x,

así que

Por lo tanto y = ue^−2x es una solución de (9.5.2.14) si y solo si

u″ + 9u = 0.

Del ejemplo 9.5.1.2, la solución general de esta ecuación es

u = c₁cos3x + c₂sen3x.

Por lo tanto, cualquier función de la forma

y = e^−2x(c₁cos3x + c₂sen3x)        (9.5.2.16)

es una solución de (9.5.2.14). Haciendo c₁ = 1 y c₂ = 0 se obtiene la solución y₁ = e^−2x cos3x. Haciendo c₁ = 0 y c₂ = 1 se obtiene la segunda solución y₂ = e^−2x sen 3x. Como y₂/y₁ = tan3x no es constante, el Teorema 9.5.1.6 implica que {y₁, y₂} es un conjunto fundamental de soluciones de (9.5.2.14), y (9.5.2.16) es la solución general.

(b)  Al imponer la condición y(0) = 2 en (9.5.2.16) se deduce que c₁ = 2. Derivando (9.5.2.16) se obtiene

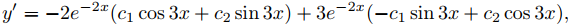
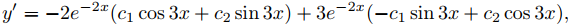
e imponer la condición inicial y′(0) = −3 aquí produce −3 = −2c₁ + 3c₂ = −4 + 3c₂, por lo que c₂ = 1/3. Por lo tanto la solución de (9.5.2.15) es

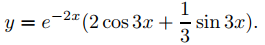
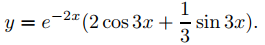
La Figura 9.5.2.3 es un gráfico de esta función.

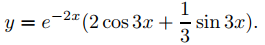
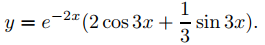
      Ahora suponga que la ecuación característica de ay″ + by′ + cy = 0 tiene raíces complejas arbitrarias; por tanto, b² − 4ac < 0 y, de acuerdo con la fórmula cuadrática (9.5.2.3), las raíces son

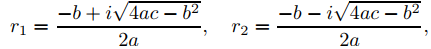
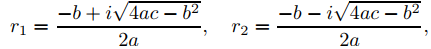
Lo que reescribimos como

r₁ = λ + iω,  r₂ = λ − iω,        (9.5.2.17)

con

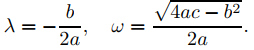
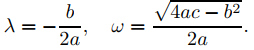
No memorices estas fórmulas. Solo recuerda que r₁ y r₂ tienen la forma (9.5.2.17), donde λ es un número real arbitrario y ω es positivo; λ y ω son las partes real e imaginaria, respectivamente, de r₁. De manera similar, λ y −ω son las partes real e imaginaria de r₂. Decimos que r₁ y r₂  son conjugados complejos, lo que significa que tienen la misma parte real y sus partes imaginarias tienen los mismos valores absolutos, pero signos opuestos.

      Como en el ejemplo 9.5.2.3, es razonable esperar que las soluciones de ay″ + by′ + cy = 0 sean combinaciones lineales de e^{(λ + iω)x}  y  e^{(λ − iω)x}. De nuevo, la notación exponencial sugiere que

e^{(λ + iω)x} = ee^λxe^iωx  y  e^{(λ − iω)x} = e^λxe^−iωx,

entonces, aunque no hemos definido e^iωx y e^−iωx, es razonable esperar que cada combinación lineal de e^(λ+iω)x y e^(λ−iω)x pueda escribirse como y = ue^λx, donde u depende de x. Para determinar u primero observamos que dado que r₁ = λ + iω y r₂ = λ − iω son las raíces de la ecuación característica, el polinomio característico p debe ser de la forma

Por lo tanto, ay″ + by′ + cy = 0 se puede escribir como

a[y″ − 2λy′ + (λ² + ω²)y] = 0.

Como a ≠ 0 esta ecuación tiene las mismas soluciones que

y″ − 2λy′ + (λ² + ω²)y = 0.        (9.5.2.18)

Para determinar u notamos que si y = ue^λx entonces

y′ = u′e^λx + λue^λx  y  y″ = u″e^λx + 2λu′e^λx + λ²ue^λx.

Sustituyendo estas expresiones en (9.5.2.18) y descartando el factor común e^λx se obtiene

(u″ + 2λu′ + λ²u) − 2λ(u′ + λu) + (λ² + ω²)u = 0,

que simplifica a

u″ + ω²u = 0.

Del ejemplo 9.5.1.2, la solución general de esta ecuación es

u = c₁cosωx + c₂senωx.

Por lo tanto, cualquier función de la forma

y = e^λx(c₁cosωx + c₂senωx)        (9.5.2.19)

es una solución de (9.5.2.18). Haciendo c₁ = 1 y c₂ = 0 aquí se obtiene la solución y₁ = e^λxcosωx. Haciendo c₁ = 0 y c₂ = 1 se obtiene una segunda solución y₂ = e^λxsenωx. Como y₂/y₁ = tanωx no es constante, el Teorema 9.5.1.6 implica que {y₁, y₂} es un conjunto fundamental de soluciones de (9.5.2.18), y (9.5.2.19) es la solución general.

Resumen

El siguiente teorema resume los resultados de esta sección.

Teorema 9.5.2.1

Sea p(r) = ar² + br + c el polinomio característico de

ay″ + by′ + cy = 0.        (9.5.2.20)

Entonces:

(a) Si p(r) = 0 tiene distintas raíces reales r₁ y r₂, entonces la solución general de (9.5.2.20) es

y = c₁e^r₁x + c₂e^r₂x.

(b) Si p(r) = 0 tiene una raíz repetida r₁, entonces la solución general de (9.5.2.20) es

y = e^r₁x(c₁ + c₂x).

(c) Si p(r) = 0 tiene raíces conjugadas complejas r₁ = λ + iω  y  r₂ = λ − iω (donde ω > 0), entonces la solución general de (9.5.2.20) es

y = e^λx(c₁cosωx + c₂senωx).  ♦