| Álgebra lineal con aplicaciones | 4. Geometría vectorial |
4.1 Vectores y rectas
En este capítulo estudiamos la geometría del espacio tridimensional. Vemos un punto en el espacio tridimensional como una flecha desde el origen hasta ese punto. Hacerlo proporciona una “imagen” del punto que realmente vale más que mil palabras. Usamos esta idea anteriormente, en la Sección 2.6, para describir rotaciones, reflejos y proyecciones del plano R². Ahora aplicamos las mismas técnicas al espacio tridimensional para examinar transformaciones similares de R³. Además, el método nos permite describir completamente todas las rectas y planos en el espacio.
Vectores en R³
Introduzca un sistema de coordenadas en un espacio tridimensional de la forma habitual. Primero elija un punto O llamado origen, luego elija tres rectas mutuamente perpendiculares a través de O, llamadas ejes x, y y z, y establezca una escala numérica en cada eje con cero en el origen. Dado un punto P en el espacio tridimensional, asociamos tres números x, y y z con P, como se describe en la figura 4.1.1. Estos números se denominan coordenadas de P, y denotamos el punto como (x, y, z) o P(x, y, z) para enfatizar la etiqueta P. El resultado se denomina sistema de coordenadas cartesiano (llamado así en honor de René Descartes, quien introdujo la idea en 1637.) para 3 espacios , y la descripción resultante del espacio tridimensional se llama geometría cartesiana.
Como en el plano, introducimos vectores identificando cada punto P(x, y, z) con el vector
en R³, representado por la flecha desde el origen hasta P como en la Figura 4.1.1. De manera informal, decimos que el punto P tiene el vector v, y que el vector v tiene el punto P. De esta manera, el espacio tridimensional se identifica con R³ , y esta identificación se hará a lo largo de este capítulo, a menudo sin comentarios.
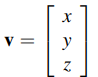
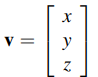
(Figura 4.1.1)
En particular, los términos “vector” y “punto” son intercambiables (Recuerde que definimos Rⁿ como el conjunto de todas las n-uplas ordenadas de números reales, y nos reservamos el derecho de denotarlas como filas o columnas.). La descripción resultante del espacio tridimensional se llama geometría vectorial. Tenga en cuenta que el origen es
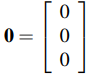
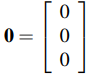
Longitud y dirección de un vector
Vamos a discutir dos propiedades geométricas fundamentales de los vectores en R³: longitud y dirección. Primero, si v es un vector con el punto P, la longitud ||v|| del vector v se define como la distancia desde el origen a P, es decir, la longitud de la flecha que representa v. Las siguientes propiedades de la longitud se usarán con frecuencia.
Teorema 4.1.1
Sea v 
un vector..
- ||v|| = √(x² + y² + z²)
- v = 0 si y sólo si ||v|| = 0
- ||a v|| = |a| ||v|| para todos los escalares a. ♦
Prueba.
Sea v el punto P(x, y, z):
1. En la Figura 4.1.2, ||v|| es la hipotenusa del triángulo rectángulo OQP, entonces ||v||² = h² + z² (por el teorema de Pitágoras). Pero h es a su vez la hipotenusa del triángulo rectángulo ORQ, entonces h² = x² + y². Ahora (1) se obtiene eliminando h² y tomando raíces cuadradas positivas.
2. Si ||v|| = 0, entonces x² + y² + z² = 0 por (1). Debido a que los cuadrados de números reales no son negativos, se sigue que x = y = z = 0, y por lo tanto que v = 0. El inverso es porque ||0|| = 0.
(Figura 4.1.2)
3. Tenemos que
entonces (1) produce
Por lo tanto, ||a v|| = √a² ||v|| y terminamos porque √a² = |a| para cualquier número real a. ◊
Por supuesto, la versión R² del teorema 4.1.1 también es válida.
Ejemplo ilustrativo 4.1.1
Cuando vemos dos vectores distintos de cero como flechas que emanan desde el origen, está claro geométricamente lo que queremos decir al afirmar que tienen la misma dirección o direcciones opuestas. Esto conduce a una nueva descripción fundamental de los vectores.
Teorema 4.1.2
Sean v ≠ 0 y w ≠ 0 vectores en R3. Entonces v = w como matrices si y solo si v y w tienen la misma dirección y la misma longitud. ♦
Es el teorema 4.1.2 el que da a los vectores su poder en ciencia e ingeniería porque muchas cantidades físicas están determinadas por su longitud y magnitud (y se denominan cantidades vectoriales). Por ejemplo, decir que un avión vuela a 200 km / h no describe hacia dónde se dirige; también debe especificarse la dirección. La rapidez y la dirección comprenden la velocidad del avión, una cantidad vectorial.
Prueba.
Si v = w, claramente tienen la misma dirección y longitud. Por el contrario, sean v y w vectores con puntos P(x, y, z) y Q(x1, y1, z1) respectivamente. Si v y w tienen la misma longitud y dirección, entonces, geométricamente, P y Q deben ser el mismo punto (ver Figura 4.1.3). Por tanto, x = x1, y = y1 y z = z1, es decir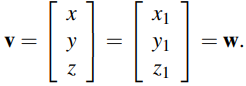
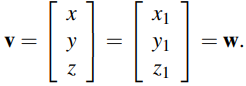
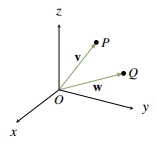
Una caracterización de un vector en términos de su longitud y dirección única se denomina descripción intrínseca del vector. El punto a tener en cuenta es que dicha descripción no depende de la elección del sistema de coordenadas en R3. Estas descripciones son importantes en las aplicaciones porque las leyes físicas a menudo se establecen en términos de vectores, y estas leyes no pueden depender del sistema de coordenadas particular utilizado para describir la situación.
Vectores geométricos
Si A y B son puntos distintos en el espacio, la flecha de A a B tiene longitud y dirección.
(Figura 4.1.4)
Por eso: