| 9. Ecuaciones diferenciales | 9.10. Sistemas lineales de ecuaciones diferenciales |
9.10.7 Variación de parámetros para sistemas de ED lineales no homogéneos
Consideremos ahora el sistema lineal no homogéneo
y′ = A(t)y + f(t),
donde A es una función matricial n × n y f es una función forzada de n vectores. Asociado con este sistema está el sistema complementario y′ = A(t)y.
El siguiente teorema es análogo a los Teoremas 9.5.3.2 y 9.9.1.5. Muestra cómo encontrar la solución general de y′ = A(t)y + f(t) si conocemos una solución particular de y′ = A(t)y + f(t) y un conjunto fundamental de soluciones de la sistema complementario. Dejamos la demostración como ejercicio (Ejercicio 21).
Teorema 9.10.7.1
Supongamos que la función matricial A de n × n y la función n-vectorial f son continuas en (a, b). Sea yp una solución particular de y′ = A(t)y + f(t) en (a, b), y sea {y1, y2, . . ., yn} sea un conjunto fundamental de soluciones de la ecuación complementaria y′ = A(t)y en (a, b). Entonces y es una solución de y′ = A(t)y + f(t) en (a, b) si y solo si
y = yp + c1y1 + c2y2 + · · · + cnyn,
donde c1, c2, . . . , cn son constantes. ♦
Encontrar una solución particular de un sistema no homogéneo
Ahora discutimos una extensión del método de variación de parámetros a sistemas lineales no homogéneos. Este método producirá una solución particular de un sistema no homogéneo y′ = A(t)y + f(t) siempre que conozcamos una matriz fundamental para el sistema complementario. Para derivar el método, suponga que Y es una matriz fundamental para el sistema complementario; es decir,
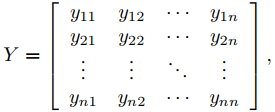
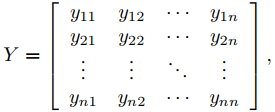
donde


es un conjunto fundamental de soluciones del sistema complementario. En la Sección 9.10.3 vimos que Y′ = A(t)Y .
Buscamos una solución particular de
y′ = A(t)y + f(t) (9.10.7.1)
de la forma
yp = Yu, (9.10.7.2)
donde se va a determinar u. Diferenciando (9.10.7.2), obtenemos


Comparando esto con (9.10.7.1) se muestra que yp = Yu es una solución de (9.10.7.1) si y solo si
Yu′ = f.
Por lo tanto, podemos encontrar una solución particular yp resolviendo esta ecuación para u′, integrando para obtener u y calculando Yu. Podemos tomar todas las constantes de integración como cero, ya que cualquier solución particular será suficiente.
El ejercicio 22 esboza una demostración de que este método es análogo al método de variación de parámetros analizado en las secciones 9.5.7 y 9.9.4 para ecuaciones lineales escalares.
Ejemplo ilustrativo 9.10.7.1
(a) Encuentre una solución particular del sistema
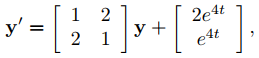
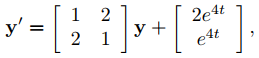
Lo que consideramos en el Ejemplo 9.10.2.1.
(b) Encuentre la solución general de (9.10.7.3)
Solución:
(a) El sistema complementario es


El polinomio característico de la matriz de coeficientes es
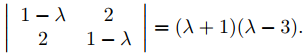
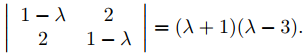
Usando el método de la Sección 9.10.4, encontramos que
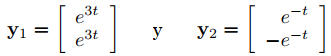
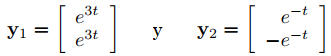
son soluciones linealmente independientes de (9.10.7.4). Por lo tanto


es una matriz fundamental para (9.10.7.4). Buscamos una solución particular yp = Yu de (9.10.7.3), donde Yu′ = f; esto es,


El determinante de Y es el Wronskiano


Por la regla de Cramer,


Por lo tanto


Integrando y tomando las constantes de integración como cero, se obtiene


de este modo


es una solución particular de (9.10.7.3).
(b) Del Teorema 9.10.7.1, la solución general de (9.10.7.3) es
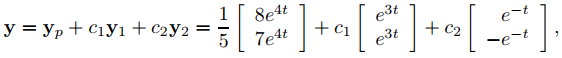
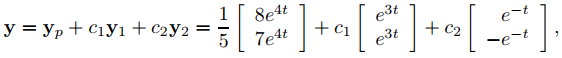
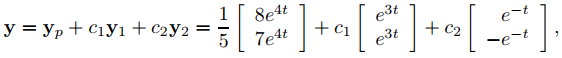
(b) Del Teorema 9.10.7.1, la solución general de (9.10.7.3) es
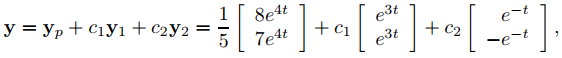
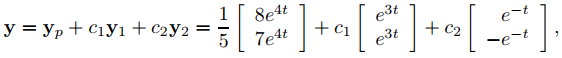
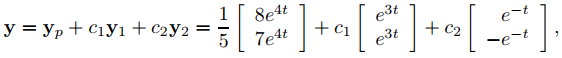
que también se puede escribir como


donde c es un vector constante arbitrario.
Escribiendo (9.10.7.5) en términos de coordenadas se obtiene


por lo que nuestro resultado es consistente con el Ejemplo 9.10.2.1. ♦
Si A no es una matriz constante, normalmente es difícil encontrar un conjunto fundamental de soluciones para el sistema y′ = A(t)y. Está más allá del alcance de este texto discutir métodos para hacer esto. Por lo tanto, en los siguientes ejemplos y en los ejercicios que involucran sistemas con matrices de coeficientes variables proporcionaremos matrices fundamentales para los sistemas complementarios sin explicar cómo se obtuvieron.
Ejemplo ilustrativo 9.10.7.2
Encuentre una solución particular de


dado que


es una matriz fundamental para el sistema complementario.
Solución:
Buscamos una solución particular yp = Yu de (9.10.7.6) donde Yu′ = f; esto es,
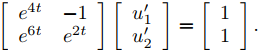
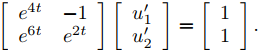
El determinante de Y es el Wronskiano


Por la regla de Cramer,


Por lo tanto


Integrando y tomando las constantes de integración como cero, se obtiene


por lo que


es una solución particular de (9.10.7.6). ♦
Ejemplo ilustrativo 9.10.7.3
Encuentre una solución particular de


dado que


es una matriz fundamental para el sistema complementario en (−∞, 0) y (0, ∞).
Solución:
Buscamos una solución particular yp = Yu de (9.10.7.7) donde Yu′ = f; esto es,
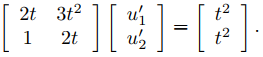
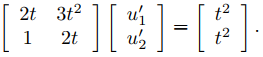
El determinante de Y es el Wronskiano


Por la regla de Cramer,


Por lo tanto


Integrando y tomando las constantes de integración como cero, se obtiene


Por lo que


es una solución particular de (9.10.7.7). ♦
Ejemplo ilustrativo 9.10.7.4
(a) Encuentre una solución particular de
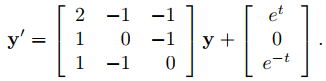
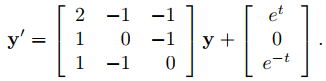
(b) Encuentre la solución general de (9.10.7.8).
Solución:
(a) El sistema complementario para (9.10.7.8) es


El polinomio característico de la matriz de coeficientes es


Usando el método de la Sección 9.10.4, encontramos que


son soluciones linealmente independientes de (9.10.7.9). Por lo tanto


es una matriz fundamental para (9.10.7.9). Buscamos una solución particular yp = Y u de (9.10.7.8), donde Y u′ = f; eso es,
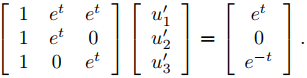
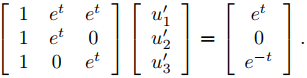
El determinante de Y es el Wronskiano


Así, por la regla de Cramer,


Por lo tanto
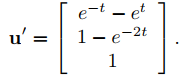
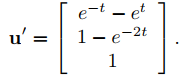
Integrando y tomando las constantes de integración como cero, se obtiene
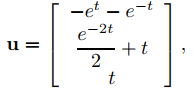
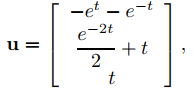
por lo que


es una solución particular de (9.10.7.8).
(b) Del Teorema 9.10.7.1 la solución general de (9.10.7.8) es


que se puede escribir como


donde c es un vector constante arbitrario. ♦
Ejemplo ilustrativo 9.10.7.5
Encuentre una solución particular de


dado que


es una matriz fundamental para el sistema complementario.
Solución:
Buscamos una solución particular de (9.10.7.10) en la forma yp = Yu, donde Yu′ = f; esto es,


El determinante de Y es el Wronskiano


Por la regla de Cramer,


Por lo tanto


Integrando y tomando las constantes de integración como cero, se obtiene


por consiguiente
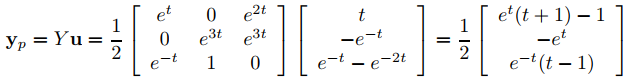
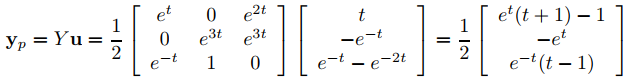
es una solución particular de (9.10.7.10). ♦
