| 9. Ecuaciones diferenciales | 9.8. La transformada de Laplace | Ejercicios propuestos para el Capítulo 9.8.2 |
9.8.2 LA TRANSFORMADA INVERSA DE LAPLACE
Definición de la transformada inversa de Laplace
En la sección 9.8.1 definimos la transformada de Laplace de f por
También diremos que f es la transformada inversa de Laplace de F, y escribiremos
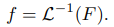
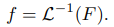
Para resolver ecuaciones diferenciales con la transformada de Laplace, debemos poder obtener f de su transformada F. Hay una fórmula para hacer esto, pero no podemos usarla porque requiere la teoría de funciones de una variable compleja. Afortunadamente, podemos usar la tabla de transformadas de Laplace para encontrar las transformaciones inversas que necesitaremos.
Ejemplo ilustrativo 9.8.2.1
Usa la tabla de transformadas de Laplace para encontrar
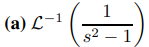
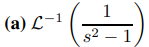
Solución:
(a) Establecer b = 1 en el par de transformación
senh bt ↔ 
muestra que
senh bt
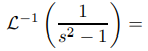
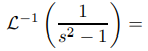
(b) Establecer ω = 3 en el par de transformación
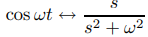
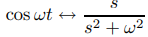
muestra que
♦
El siguiente teorema nos permite encontrar transformadas inversas de combinaciones lineales de transformadas dadas en la tabla. Omitimos la prueba.
Teorema 9.8.2.1 [Propiedad de linealidad]
Si F1, F2,. . ., Fn son transformadas de Laplace y c1, c2,. . . , cn son constantes, entonces
♦
Ejemplo ilustrativo 9.8.2.2
Hallar
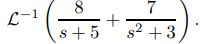
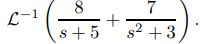
Solución:
De la tabla de transformadas de Laplace en la Sección 9.8.8,
y 
Al aplicar el teorema 9.8.2.1 con a = −5 y ω = √3, se obtiene
Ejemplo ilustrativo 9.8.2.3
Hallar
Solución:
Completando el cuadrado en el denominador se obtiene
Debido a la forma del denominador, consideramos los pares de transformadas
y 
y se tiene que
OBSERVACIÓN: A menudo escribimos transformadas de Laplace inversas de funciones específicas sin indicar explícitamente cómo se obtienen. En tales casos, debe consultar la tabla de transformadas de Laplace en la Sección 9.8.8.
Transformadas inversas de Laplace de funciones racionales
El uso de la transformada de Laplace para resolver ecuaciones diferenciales a menudo requiere encontrar la transformada inversa de una función racional
donde P y Q son polinomios en s sin factores comunes. Dado que se puede demostrar que lims → ∞ F(s) = 0 si F es una transformada de Laplace, solo necesitamos considerar el caso donde grado (P) < grado (Q). Para obtener 
(F), encontramos la expansión en fracciones parciales de F, obtenemos transformadas inversas de los términos individuales en la expansión de la tabla de transformadas de Laplace y usamos la propiedad de linealidad de la transformada inversa. Los siguientes dos ejemplos ilustran esto.
Ejemplo ilustrativo 9.8.2.4
Encuentre la transformada inversa de Laplace de
(9.8.2.1)
Solución:
(MÉTODO 1) Factorizar el denominador en (9.8.2.1) produce
(9.8.2.2)
La forma para la expansión en fracciones parciales es
(9.8.2.3)
Multiplicando esto por (s − 1)(s − 2) se obtiene
3s + 2 = (s − 2)A + (s − 1)B.
Establecer s = 2 produce B = 8 y establecer s = 1 produce A = −5. Por lo tanto
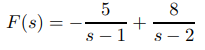
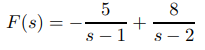
y
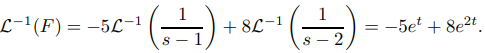
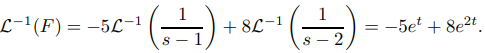
(MÉTODO 2) Realmente no tenemos que multiplicar (9.8.2.3) por (s − 1)(s − 2) para calcular A y B. Podemos obtener A simplemente ignorando el factor s − 1 en el denominador de (9.8.2.2) y estableciendo s = 1 al igualar A a la fracción que queda en el miembro derecho; de donde,
(9.8.2.4)
De manera similar, podemos obtener B ignorando el factor s − 2 en el denominador de (9.8.2.2) y estableciendo s = 2 al igualar B a la fracción que queda en el miembro derecho; de donde,
(9.8.2.5)
Para justificar esto, observamos que multiplicar (9.8.2.3) por s − 1 produce
y establecer s = 1 conduce a (9.8.2.4). De manera similar, al multiplicar (9.8.2.3) por s − 2 se obtiene
y establecer s = 2 conduce a (9.8.2.5). (No es necesario escribir las dos últimas ecuaciones. Las escribimos solo para justificar el procedimiento de atajo indicado en (9.8.2.4) y (9.8.2.5).) ♦
El atajo empleado en la segunda solución del ejemplo 9.8.2.4 es el método de Heaviside. El siguiente teorema establece este método formalmente. Para obtener una demostración y una extensión de este teorema, consulte el Ejercicio 10 de esta sección.
Teorema 9.8.2.2 Método de Heaviside
Suponga que
(9.8.2.6)
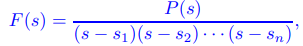
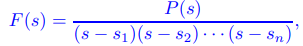
donde s1, s2,. . ., sn son distintos y P es un polinomio de grado menor que n. Entonces
donde Ai se puede calcular a partir de (9.8.2.6) ignorando el factor s − si y estableciendo s = si en otro lugar. ♦
Ejemplo ilustrativo 9.8.2.5
Encuentre la transformada inversa de Laplace de
(9.8.2.7)
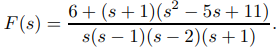
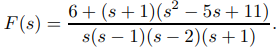
Solución:
La expansión en fracciones parciales de (9.8.2.7) tiene la forma
(9.8.2.8)
Para encontrar A, ignoramos el factor s en el denominador de (9.8.2.7) y establecemos s = 0 en otro lugar. Esto produce
De manera similar, los otros coeficientes vienen dados por
y
Por lo tanto
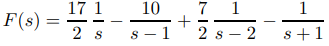
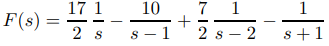
y
OBSERVACIÓN: No “multiplicamos” el numerador en (9.8.2.7) antes de calcular los coeficientes en (9.8.2.8), ya que no simplificaría los cálculos.
Ejemplo ilustrativo 9.8.2.6
Encuentre la transformada inversa de Laplace de
(9.8.2.9)
Solución:
La forma para la expansión en fracciones parciales es
(9.8.2.10)
Debido al factor repetido (s + 2)2 en (9.8.2.9), el método de Heaviside no funciona. En cambio, encontramos un denominador común en (9.8.2.10). Esto produce
(9.8.2.11)
Si (9.8.2.9) y (9.8.2.11) van a ser equivalentes, entonces
(9.8.2.12)
Los dos lados de esta ecuación son polinomios de grado dos. Según un teorema de álgebra, serán iguales para todos los s si son iguales para tres valores distintos de s. Podemos determinar A, B y C eligiendo valores convenientes de s.
El lado izquierdo de (9.8.2.12) sugiere que tomamos s = −2 para obtener C = −8 y s = −1 para obtener A = 2. Ahora podemos elegir cualquier tercer valor de s para determinar B. Tomando s = 0 produce 4A + 2B + C = −12. Dado que A = 2 y C = −8, esto implica que B = −6. Por lo tanto
y
Ejemplo ilustrativo 9.8.2.7
Encuentre la transformada inversa de Laplace de
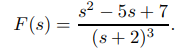
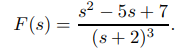
Solución:
La forma para la expansión en fracciones parciales es
La forma más fácil de obtener A, B y C es expandir el numerador en potencias de s + 2. Esto produce
s2 − 5s + 7 = [(s + 2) − 2]2 − 5[(s + 2) − 2] + 7 = (s + 2)2 − 9(s + 2) + 21.
Por lo tanto
y
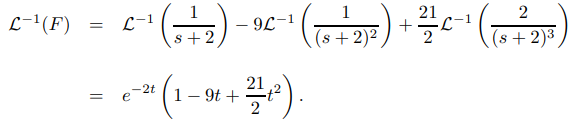
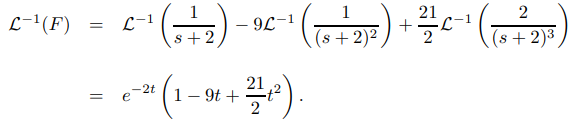
Ejemplo ilustrativo 9.8.2.8
Encuentre la transformada inversa de Laplace de
(9.8.2.13)
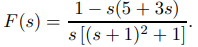
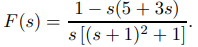
Solución:
Una forma para la expansión en fracciones parciales de F es
(9.8.2.14)
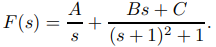
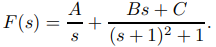
Sin embargo, vemos en la tabla de transformadas de Laplace que la transformada inversa de la segunda fracción a la derecha de (9.8.2.14) será una combinación lineal de las transformadas inversas
y 
de
y 
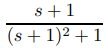
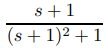
respectivamente. Por lo tanto, en lugar de (9.8.2.14) escribimos
(9.8.2.15)
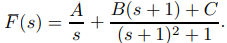
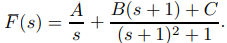
Encontrar un denominador común produce
(9.8.2.16)
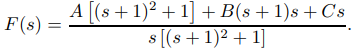
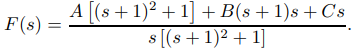
Si (9.8.2.13) y (9.8.2.16) deben ser equivalentes, entonces
A(s + 1)2 + 1 + B(s + 1)s + Cs = 1 − s(5 + 3s).
Esto es cierto para todos los s si es cierto para tres valores distintos de s. Al elegir s = 0, −1 y 1 se obtiene el sistema
Resolver este sistema produce
Por tanto, de (9.8.2.15),
Por lo tanto
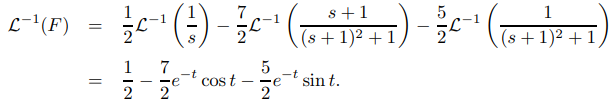
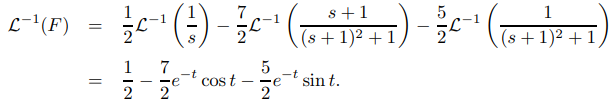
Ejemplo ilustrativo 9.8.2.9
Encuentre la transformada inversa de Laplace de
(9.8.2.17)
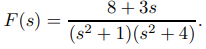
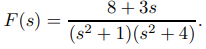
Solución:
Una forma para la expansión en fracciones parciales de F es
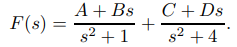
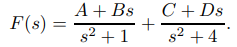
Los coeficientes A, B, C y D se pueden obtener encontrando un denominador común y equiparando el numerador resultante con el numerador de (9.8.2.17). Sin embargo, dado que no hay una primera potencia de s en el denominador de (9.8.2.17), hay una forma más fácil: la expansión de
se puede obtener rápidamente utilizando el método de Heaviside para expandir
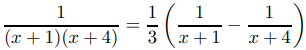
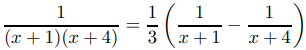
y luego estableciendo x = s2 para obtener
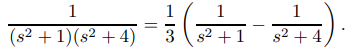
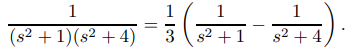
Multiplicando esto por 8 + 3s se obtiene
Por lo tanto
USANDO TECNOLOGÍA
Algunos paquetes de software que hacen álgebra simbólica pueden encontrar expansiones de fracciones parciales muy fácilmente. Le recomendamos que utilice un paquete de este tipo si tiene uno disponible, pero solo después de haber realizado suficientes expansiones de fracciones parciales por su cuenta para dominar la técnica.
Excelente hermano, me sirvió de mucho y esta completa, gracias y sigue publicando mas. Saludos desde Venezuela
Gracias por el comentario. Puede acceder a la solución de ejercicios sobre la transformada inversa de Laplace desde el siguiente PDF https://calculo21.com/ejercicios-resueltos-del-capitulo-9/ 👀