| 7. Sucesiones y series infinitas | Ejercicios propuestos para el Capítulo 7.4 |
PRUEBAS DE COMPARACIÓN
Objetivos de aprendizaje:
7.4.1. Use la prueba de comparación para probar la convergencia de una serie.
7.4.2. Use la prueba de comparación por límite para determinar la convergencia de una serie.
Hemos visto que la prueba de la integral nos permite determinar la convergencia o divergencia de una serie comparándola con una integral impropia relacionada. En esta sección, mostramos cómo usar las pruebas de comparación para determinar la convergencia o divergencia de una serie comparándola con una serie cuya convergencia o divergencia es conocida. Por lo general, estas pruebas se utilizan para determinar la convergencia de series que son similares a las series geométricas o series p.
Prueba de comparación
En las dos secciones anteriores, discutimos dos grandes clases de series: series geométricas y series p. Sabemos exactamente cuándo convergen estas series y cuándo divergen. Aquí mostramos cómo usar la convergencia o divergencia de estas series para probar la convergencia o divergencia de otras series, utilizando un método llamado prueba de comparación.
Por ejemplo, considere la serie
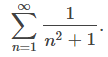
Esta serie se parece a la serie convergente
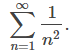
Dado que los términos en cada una de las series son positivos, la secuencia de sumas parciales para cada serie es monótonamente creciente. Además, dado que
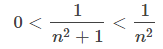
para todos los enteros positivos n, la k-ésima suma parcial Sk de
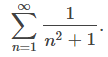
satisface
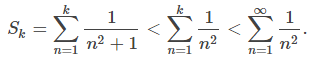
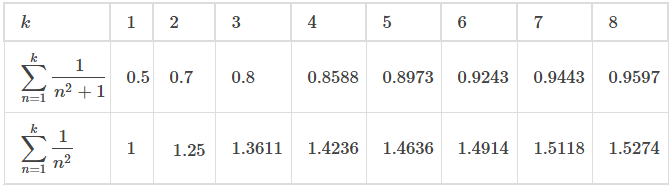
(Consulte la Figura 7.4_1 (a) y la Tabla 7.4_1.) Dado que la serie de la derecha converge, la secuencia {Sk} está acotada inferiormente. Concluimos que {Sk} es una secuencia monótona creciente que está acotada inferiormente. Por lo tanto, según el Teorema de convergencia monótona, {Sk} converge, y por lo tanto la serie
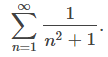
converge.
Del mismo modo, considere la serie
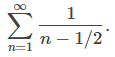
Esta serie se parece a la serie divergente
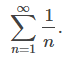
La secuencia de sumas parciales para cada serie es monótona creciente y además
por cada entero positivo n. Por lo tanto, la k-ésima suma parcial Sk de
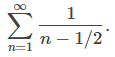
satisface
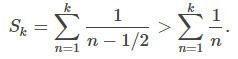
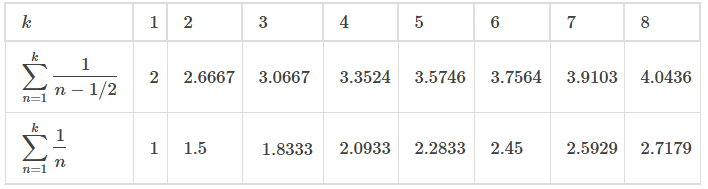
(Ver Figura 7.4_2 (b) y Tabla 7.4_2.). Dado que la serie
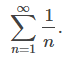
diverge al infinito, la secuencia de sumas parciales
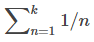
es no acotada. En consecuencia, {Sk} es una secuencia no acotada y, por lo tanto, diverge. Concluimos que
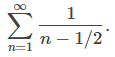
diverge.
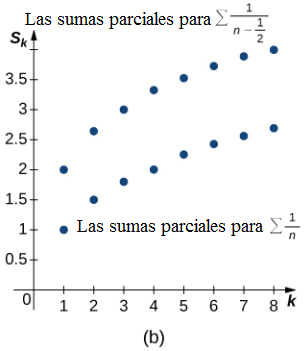
(Figura 7.4_1 (a) Cada una de las sumas parciales para la serie dada es menor que la suma parcial correspondiente para la serie p convergente. (b) Cada una de las sumas parciales para la serie dada es mayor que la suma parcial correspondiente para la serie armónica divergente.)
TEOREMA 7.4_1. Prueba de comparación
i. Supongamos que existe un entero \( \mathit{N} \) tal que \( 0 \leq \mathit{a_n} \leq \mathit{b_n} \) para todo \( \mathit{n} \geq \mathit{N} \). Si \( \sum\limits_{n=1}^{\infty} \mathit{b_n} \) converge, entonces \( \sum\limits_{n=1}^{\infty} \mathit{a_n} \) también converge.
ii. Supongamos que existe un entero \( \mathit{N} \) tal que \( \mathit{a_n} \geq \mathit{b_n} \geq 0 \) para todo \( \mathit{n} \geq \mathit{N} \). Si \( \sum\limits_{n=1}^{\infty} \mathit{b_n} \) diverge, entonces \( \sum\limits_{n=1}^{\infty} \mathit{a_n} \) también diverge.
♦
Demostración
Demostramos la parte \( \mathit{i} \). La demostración de la parte \( \mathit{ii} \) es la contrarrecíproca de la parte \( \mathit{i} \). Sea \( \{ \mathit{S_k} \} \) la sucesión de sumas parciales asociada con \( \sum\limits_{n=1}^{\infty} \mathit{a_n} \), y sea \( \mathit{L} = \sum\limits_{n=1}^{\infty} \mathit{b_n} \). Dado que los términos \( \mathit{a_n} \geq 0 \), \[ \mathit{S_k} = \mathit{a_1} + \mathit{a_2} + \dots + \mathit{a_k} \leq \mathit{a_1} + \mathit{a_2} + \dots + \mathit{a_k} + \mathit{a_{k+1}} = \mathit{S_{k+1}}. \] Por lo tanto, la sucesión de sumas parciales es creciente. Además, dado que \( \mathit{a_n} \leq \mathit{b_n} \) para todo \( \mathit{n} \geq \mathit{N} \), \[ \sum\limits_{n=N}^{k} \mathit{a_n} \leq \sum\limits_{n=N}^{k} \mathit{b_n} \leq \sum\limits_{n=1}^{\infty} \mathit{b_n} = \mathit{L}. \] Por lo tanto, para todo \( \mathit{k} \geq 1 \), \[ \mathit{S_k} = (\mathit{a_1} + \mathit{a_2} + \dots + \mathit{a_{N-1}}) + \sum\limits_{n=N}^{k} \mathit{a_n} \leq (\mathit{a_1} + \mathit{a_2} + \dots + \mathit{a_{N-1}}) + \mathit{L}. \] Dado que \( \mathit{a_1} + \mathit{a_2} + \dots + \mathit{a_{N-1}} \) es un número finito, concluimos que la sucesión \( \{ \mathit{S_k} \} \) está acotada superiormente. Por lo tanto, \( \{ \mathit{S_k} \} \) es una sucesión creciente que está acotada superiormente. Por el Teorema de Convergencia Monótona, concluimos que \( \{ \mathit{S_k} \} \) converge, y por lo tanto la serie \( \sum\limits_{n=1}^{\infty} \mathit{a_n} \) converge.♦
Para usar la prueba de comparación para determinar la convergencia o divergencia de una serie \( \sum\limits_{n=1}^{\infty} \mathit{a_n} \), es necesario encontrar una serie adecuada con la cual compararla. Dado que conocemos las propiedades de convergencia de las series geométricas y las \( p \)-series, estas series suelen ser utilizadas. Si existe un entero \( \mathit{N} \) tal que, para todo \( \mathit{n} \geq \mathit{N} \), cada término \( \mathit{a_n} \) es menor que cada término correspondiente de una serie convergente conocida, entonces \( \sum\limits_{n=1}^{\infty} \mathit{a_n} \) converge. De manera similar, si existe un entero \( \mathit{N} \) tal que, para todo \( \mathit{n} \geq \mathit{N} \), cada término \( \mathit{a_n} \) es mayor que cada término correspondiente de una serie divergente conocida, entonces \( \sum\limits_{n=1}^{\infty} \mathit{a_n} \) diverge.
EJEMPLO ILUSTRATIVO 7.4_1. Usando la prueba de comparación
Para cada una de las siguientes series, use la prueba de comparación para determinar si la serie converge o diverge.
Solución:
a. Comparar con
Ya que esta serie es una serie p con p = 3, converge. Además,
para cada entero positivo n. Por lo tanto, podemos concluir que la serie dada
converge.
b. Comparar con
Debido a que esta serie es una serie geométrica con r = 1/2 y |1/2| < 1, converge. Además,
para cada entero positivo n. Por lo tanto, vemos que la serie dada
converge.
c. Comparar con
Dado que 
para cada entero n ≥ 2 y
diverge, tenemos que la serie dada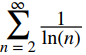
diverge. ♦
Ejercicio de control 7.4.1
Usa la prueba de comparación para determinar si la serie \( \sum\limits_{n=1}^{\infty} \frac{\displaystyle n}{\displaystyle n^{3} + n + 1} \) converge o diverge.♦
Prueba de comparación del límite
La prueba de comparación funciona muy bien si podemos encontrar una serie comparable que satisfaga la hipótesis de la prueba. Sin embargo, a veces encontrar una serie apropiada puede ser difícil. Considera la serie
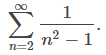
Es natural comparar esta serie con la serie convergente
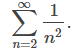
Sin embargo, esta serie no satisface la hipótesis necesaria para usar la prueba de comparación porque
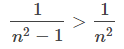
para todos los enteros n ≥2. Aunque podríamos buscar una serie diferente con la que comparar
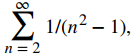
en su lugar, mostramos cómo podemos usar la prueba de comparación de límites para comparar
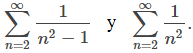
Examinemos la idea detrás de la prueba de comparación del límite. Considere dos series
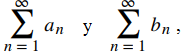
con términos positivos an y bn y evaluar el
\[ \lim_{n \to \infty} \frac{a_n}{b_n} \]Si
\[ \lim_{n \to \infty} \frac{a_n}{b_n} = L \neq 0 \]entonces, para n suficientemente grande, an ≈ Lbn. Por lo tanto, ambas series convergen o ambas series divergen. Para las series
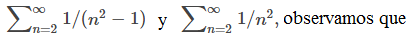
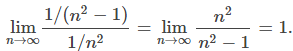
Dado que
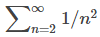
converge, concluimos que
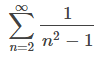
converge.
La prueba de comparación del límite se puede usar en otros dos casos. Supongamos que
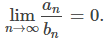
En este caso, {an / bn} es una secuencia acotada. Como resultado, existe una constante M tal que an ≤ Mbn. Por lo tanto,
\[ \text{si } \sum_{n=1}^{\infty} b_n \text{ converge, entonces } \sum_{n=1}^{\infty} a_n \text{ converge.} \]Por otro lado, supongamos que
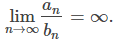
En este caso, {an/bn} es una secuencia no acotada. Por lo tanto, para cada constante M existe un número entero N tal que an ≥ Mbn para todos los n ≥ N. Por lo tanto,
\[ \text{si } \sum_{n=1}^{\infty} b_n \text{ diverge, entonces } \sum_{n=1}^{\infty} a_n \text{ también diverge.} \]TEOREMA 7.4_2. Prueba de comparación de límites
Sean \(\mathit{a}_n, \mathit{b}_n \geq 0\) para toda \(\mathit{n} \geq 1\). \[ \begin{aligned} 1. &\ \text{Si } \lim_{n \to \infty} \frac{\mathit{a}_n}{\mathit{b}_n} = \mathit{L} \neq 0, \text{ entonces } \sum_{n=1}^{\infty} \mathit{a}_n \text{ y } \sum_{n=1}^{\infty} \mathit{b}_n \text{ ambas convergen o ambas divergen.} \\ 2. &\ \text{Si } \lim_{n \to \infty} \frac{\mathit{a}_n}{\mathit{b}_n} = 0 \text{ y } \sum_{n=1}^{\infty} \mathit{b}_n \text{ converge, entonces } \sum_{n=1}^{\infty} \mathit{a}_n \text{ converge.} \\ 3. &\ \text{Si } \lim_{n \to \infty} \frac{\mathit{a}_n}{\mathit{b}_n} = \infty \text{ y } \sum_{n=1}^{\infty} \mathit{b}_n \text{ diverge, entonces } \sum_{n=1}^{\infty} \mathit{a}_n \text{ diverge.} \end{aligned} \]♦
Tenga en cuenta que si an/bn → 0 y
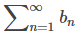
diverge, la prueba de comparación de límites no proporciona información. Del mismo modo, si an/bn → ∞ y
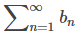
converge, la prueba tampoco proporciona información. Por ejemplo, considere las dos series
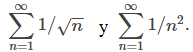
Estas series son ambas series p con p = 1/2 y p = 2, respectivamente. Como p = 1/2 < 1, la serie
diverge.
Por otro lado, ya que p = 2 > 1, la serie
converge.
Sin embargo, supongamos que intentamos aplicar la prueba de comparación de límites, utilizando la serie p convergente
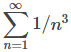
como nuestra serie de comparación. Primero, vemos que
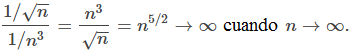
Del mismo modo, vemos que
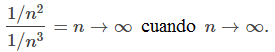
Por lo tanto, si an/bn → ∞ cuando
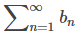
converge, no obtenemos ninguna información sobre la convergencia o divergencia de la serie
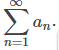
EJEMPLO ILUSTRATIVO 7.4_2. Uso de la prueba de comparación de límites
Para cada una de las siguientes series, use la prueba de comparación de límites para determinar si la serie converge o diverge. Si la prueba no se aplica, dígalo.
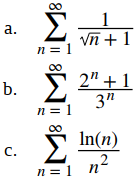
Solución:
a. Compare esta serie con
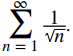
Calcular
Por la prueba de comparación de límites, ya que
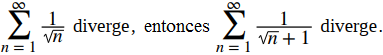
b. Compare esta serie con
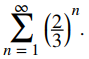
Observamos que
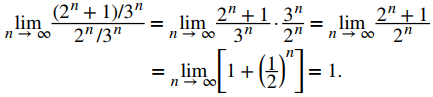
Por lo tanto,
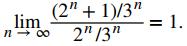
Debido a que
converge, concluimos que
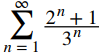
converge.
c. Como lnn < n, es adecuado comparar con
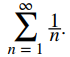
Observamos que
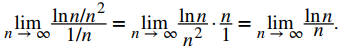
Para evaluar limn → ∞ lnn/n, evalúe el límite cuando x → ∞ de la función de valor real ln(x)/x. Estos dos límites son iguales, y hacer este cambio nos permite usar la regla de L’Hôpital. Obtenemos
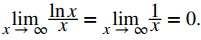
Por lo tanto, limn → ∞ lnn/n = 0 y, en consecuencia,
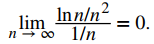
Como el límite es 0 pero
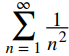
diverge, la prueba de comparación de límites no proporciona ninguna información.
Comparar en su lugar con
En este caso,
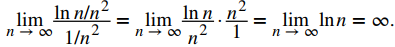
Como el límite es ∞ pero
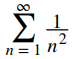
converge, la prueba aún no proporciona ninguna información.
Así que ahora intentamos una serie entre las dos que ya probamos. Si elegimos la serie
observamos que
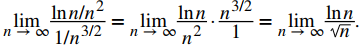
Como se indicó anteriormente, para evaluar limn → ∞ lnn/√n, evalúe el límite cuando x → ∞ de la función de valor real lnx/√x. Usando la regla de L’Hôpital,
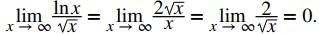
Como el límite es 0 y
converge, podemos concluir que
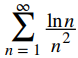
converge. ♦
Ejercicio de control 7.4.2
Use la prueba de comparación por el límite para determinar si la serie \( \sum_{n=1}^{\infty} \frac{5n}{3n+2} \) converge o diverge.♦