LÍMITES EN EL INFINITO Y ASÍNTOTAS : Objetivos de aprendizaje
4.6.1. Calcular el límite de una función a medida que x aumenta o disminuye sin límite.
4.6.2. Reconocer una asíntota horizontal en la gráfica de una función.
4.6.3. Estimar el comportamiento final de una función a medida que x aumenta o disminuye sin límite.
4.6.4. Reconocer una asíntota oblicua en la gráfica de una función.
4.6.5. Analizar una función y sus derivados para dibujar su gráfica.
Hemos mostrado cómo usar las derivadas primera y segunda de una función para describir la forma de su gráfica. Para graficar una función f definida en un dominio ilimitado, también necesitamos conocer el comportamiento de f cuando x → ± ∞. En esta sección, definimos límites en el infinito y mostramos cómo estos límites afectan la gráfica de una función. Al final de esta sección, describimos una estrategia para graficar una función arbitraria f.
Límites en el infinito
Comenzamos examinando lo que significa que una función tenga un límite finito en el infinito. Luego estudiamos la idea de una función con un límite infinito en el infinito. En esta sección tratamos las asíntotas horizontales y oblicuas.
Límites en infinito y asíntotas horizontales
Recuerde que


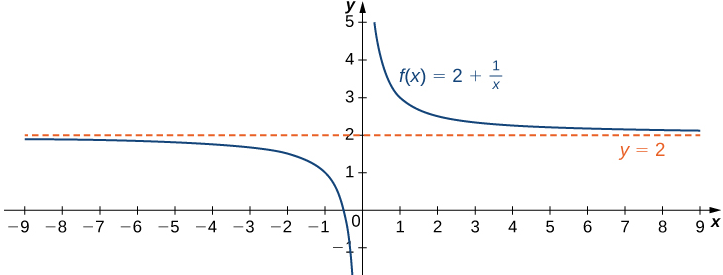
significa que f(x) se aproxima arbitrariamente a L siempre que x esté lo suficientemente cerca de a. Podemos extender esta idea a límites en el infinito. Por ejemplo, considere la función f(x) = 2 + 1/x. Como se puede ver gráficamente en la Figura 4.21 y numéricamente en la Tabla 4.2, a medida que los valores de x aumentan, los valores de f(x) se aproximan a 2. Decimos que el límite a medida que x se aproxima a ∞ de f(x) es 2 y escribimos


Del mismo modo, para x < 0, conforme los valores de |x| aumentan, los valores de f (x) se acercan a 2. Decimos que el límite a medida que x se acerca a −∞ de f(x) es 2 y escribimos



| x | 1010 | 100100 | 1,0001,000 | 10,00010,000 |
| 2 + 1/x | 2.12.1 | 2.012.01 | 2.0012.001 | 2.00012.0001 |
| x | −10−10 | −100−100 | −1000−1000 | −10,000−10,000 |
| 2 + 1/x | 1.91.9 | 1.991.99 | 1.9991.999 | 1.9999 |
Tabla 4.2 Valores de la función f (x) = 2 + 1/x cuando x → ± ∞
Más generalmente, para cualquier función f, decimos que el límite cuando x → ∞ de f (x) es L si f(x) se acerca arbitrariamente a L siempre que x sea suficientemente grande. En ese caso, escribimos


De manera similar, decimos que el límite como x → −∞ de f(x) es L si f(x) se acerca arbitrariamente a L siempre que x < 0 y |x| es suficientemente grande. En ese caso, escribimos


Ahora establecemos la definición de una función que tiene un límite en el infinito.
Definición 4.6.1 (Informal). Límite en el infinito
Si los valores de f(x) se vuelven acercan arbitrariamente a L cuando x se hace lo suficientemente grande, decimos que la función f tiene un límite en el infinito y escribimos


Si los valores de f(x) se vuelven acercan arbitrariamente a L para x < 0 como |x| se vuelve suficientemente grande, decimos que la función f tiene un límite en infinito negativo y escribimos


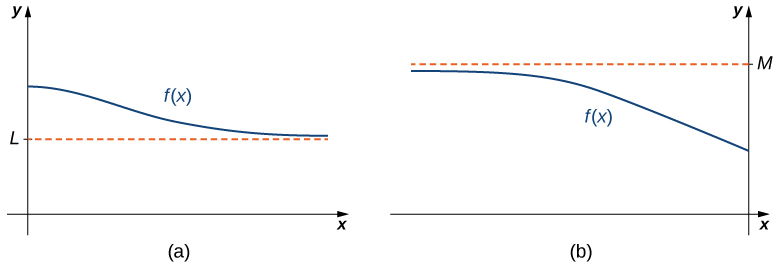
Si los valores de f(x) se están acercando arbitrariamente a algún valor finito L cuando x → ∞ o x → −∞, la gráfica de f se aproxima a la recta y = L. En ese caso, la recta y = L es una asíntota horizontal de f (Figura 4.22). Por ejemplo, para la función f(x) = 1/x, dado que


la recta y = 0 es una asíntota horizontal de f(x) = 1/x.
Definición 4.6.2. Asíntota horizontal
Si


decimos que la línea y = L es una asíntota horizontal de f.

Una función no puede cruzar una asíntota vertical porque la gráfica debe acercarse al infinito (o −∞) desde al menos una dirección a medida que x se acerca a la asíntota vertical. Sin embargo, una función puede cruzar una asíntota horizontal. De hecho, una función puede cruzar una asíntota horizontal un número ilimitado de veces. Por ejemplo, la función f (x) = (cosx)/x + 1 que se muestra en la Figura 4.23 cruza la asíntota horizontal y = 1 un número infinito de veces a medida que oscila alrededor de la asíntota con una amplitud cada vez menor.


Las leyes de límites algebraicos y el teorema de compresión que presentamos en Introducción a los límites también se aplican a los límites en el infinito.

Hola tengo el siguiente ejercicio
Lim. (1+a/x)^x
x-> ∞
Dónde a> 1
Debo calcular el límite por aproximación a la izquierda el límite me da e^a ahora mi pregunta es si cambio los valores de a el límite cambia según el enunciado, si tomo arbitrariamente un calor para a el límite por decir a= 4 la tabla si se puede calcular, la pregunta es sí puedo hacer eso??
Hola Martín.
Por supuesto que si.
Lim (1+a/x)^x
x-> ∞
es e^a
Y
Lim (1+4/x)^x
x-> ∞
es e^4
Y
Lim (1+215/x)^x
x-> ∞
es e^215
.
.
.
Saludos!
Hola, me puede explicar de manera sencilla cual es la relaciona entre los límites al infinito y limites infinitos con las asíntotas verticales y horizontales de las funciones. Por favor
Hola Marcela. Existen tres tipos de asíntotas: Horizontales, verticales y oblicuas.
Asíntotas horizontales: Si el límite de una función cuando la variable independiente x tiende al infinito es un valor constante se dice que la función tiene una asíntota horizontal. Por ejemplo, en la función f(x) = 1/x, cuando x tiende a más infinito, la función la función f tiende a 0; por lo tanto, y = 0 es una asíntota horizontal de f.
Asíntotas verticales: Si una función tiende a infinito cuando la variable independiente tiende a un valor constante, x = a, se dice que la función tiene una asíntota vertical. Por ejemplo, en la función f(x) = 1/(x+1), cuando x tiende a −1 por la derecha la función tiende a +∞; por lo tanto, x = –1 es una asíntota vertical de f.
Asíntotas oblicuas: En las funciones racionales impropias, donde el grado del numerador es una unidad mayor que el grado del denominador, ocurren asíntotas oblicuas. Estas asíntotas se obtienen efectuando la división de los polinomios, el cociente, que es una función lineal, es la asíntota oblicua. Por ejemplo, en la función f(x) = (x³ + x + 1)/(x² + 1) = x + 1/(x² + 1), y = x es una asíntota oblicua.
Hola
Hola María
¿Qué necesita, en qué le puedo colaborar? 👀👍
Saludos! 😺
Hola a todos, los contenidos proporcionados en este sitio web son realmente impresionantes para el aprendizaje de las personas interesadas en el Cálculo infinitesimal, sigan con el buen trabajo compañeros.