Superficies cuadráticas

SUPERFICIES CUADRÁTICAS: Objetivos de aprendizaje

10.6.1. Identifique un cilindro como un tipo de superficie tridimensional.
10.6.2. Reconocer las características principales de los elipsoides, paraboloides e hiperboloides.
10.6.3. Use trazas para dibujar las intersecciones de superficies cuadráticas con los planos de coordenadas.

Hemos estado explorando vectores y operaciones con vectores en un espacio tridimensional, y hemos desarrollado ecuaciones para describir rectas, planos y esferas. En esta sección, usamos nuestro conocimiento de planos y esferas, que son ejemplos de figuras tridimensionales llamadas superficies, para explorar una variedad de otras superficies que se pueden graficar en un sistema de coordenadas tridimensional.

Identificando cilindros

La primera superficie que examinaremos es el cilindro. Aunque la mayoría de la gente piensa inmediatamente en una tubería hueca o una pajita de refresco cuando escuchan la palabra cilindro, aquí usamos el amplio significado matemático del término. Como hemos visto, las superficies cilíndricas no tienen que ser circulares. Un conducto de calentamiento rectangular es un cilindro, al igual que una estera de yoga enrollada, cuya sección transversal tiene forma de espiral.

En el plano de coordenadas bidimensional, la ecuación

describe una circunferencia centrada en el origen con radio 3. En el espacio tridimensional, esta misma ecuación representa una superficie. Imagine copias de una circunferencia apiladas una encima de la otra con centro en el eje z (Figura 106_1), formando un tubo hueco. Luego podemos construir un cilindro a partir del conjunto de rectas paralelas al eje z que pasan a través de la circunferencia

en el plano xy, como se muestra en la figura. De esta manera, cualquier curva en uno de los planos de coordenadas puede extenderse para convertirse en una superficie.

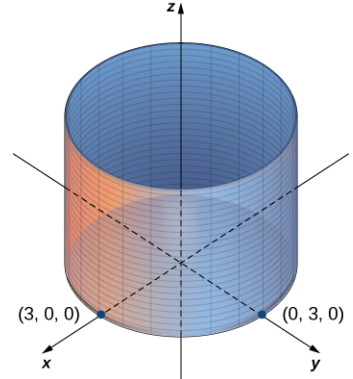
Figura 106_1 En el espacio tridimensional, la gráfica de la ecuación x^2 + y^2 = 9 es un cilindro con radio 3 centrado en el eje z. Continúa indefinidamente en las direcciones positivas y negativas.

DEFINICIÓN. Cilindro Un conjunto de rectas paralelas a una recta dada que pasa a través de una curva dada se conoce como superficie cilíndrica o cilindro. Las rectas paralelas se llaman resoluciones.

A partir de esta definición, podemos ver que todavía tenemos un cilindro en el espacio tridimensional, incluso si la curva no es una circunferencia. Cualquier curva puede formar un cilindro, y las resoluciones que componen el cilindro pueden ser paralelas a cualquier recta dada (Figura 10.6_2).

EJEMPLO ILUSTRATIVO 10.6_1. Graficando Superficies Cilíndricas

Dibuja los gráficos de las siguientes superficies cilíndricas.

Solución:
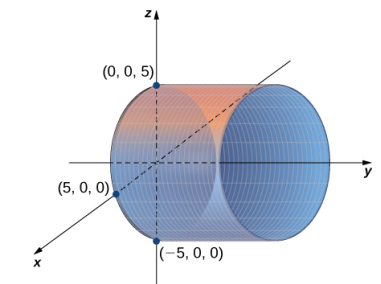
a. La variable y puede tomar cualquier valor sin límite. Por lo tanto, las líneas que gobiernan esta superficie son paralelas al eje y. La intersección de esta superficie con el plano xz forma una circunferencia centrada en el origen con radio 5 (ver la siguiente figura).

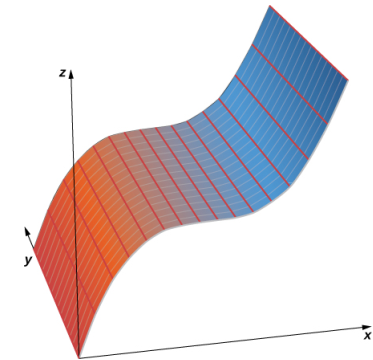
b. En este caso, la ecuación contiene las tres variables, x, y y z, por lo que ninguna de las variables puede variar arbitrariamente. La forma más fácil de visualizar esta superficie es usar una utilidad de gráficos por computadora (consulte la siguiente figura).

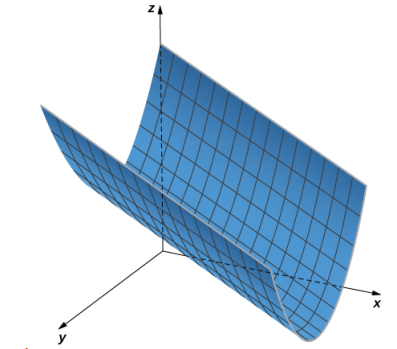
c. En esta ecuación, la variable z puede tomar cualquier valor sin límite. Por lo tanto, las líneas que componen esta superficie son paralelas al eje z. La intersección de esta superficie con los contornos del plano xy curva y = senx (ver la siguiente figura).

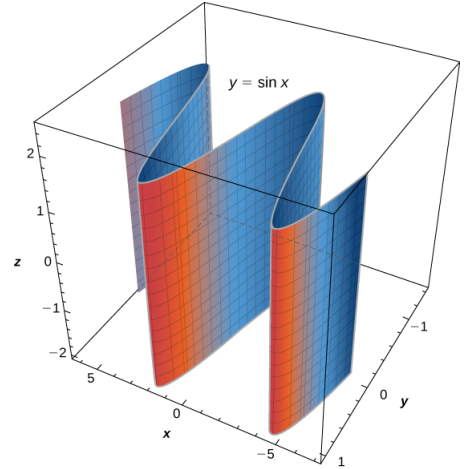
Al dibujar superficies, hemos visto que es útil dibujar la intersección de la superficie con un plano paralelo a uno de los planos de coordenadas. Estas curvas se llaman trazas. Podemos verlos en la gráfica del cilindro en la figura 10.6_6.

DEFINICIÓN. Trazas Las trazas de una superficie son las secciones transversales creadas cuando la superficie se cruza con un plano paralelo a uno de los planos de coordenadas.

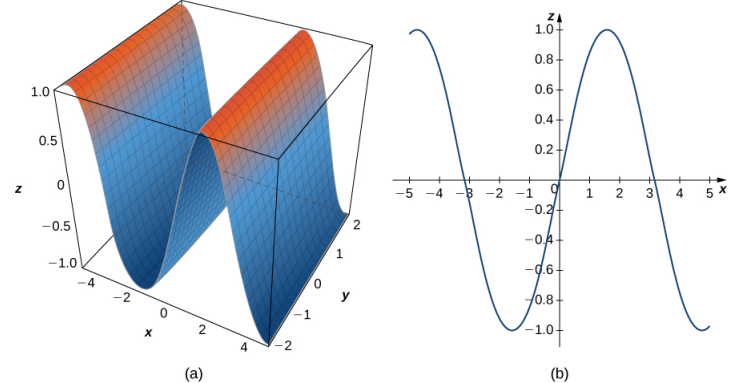
Las trazas son útiles para dibujar superficies cilíndricas. Sin embargo, para un cilindro en tres dimensiones, solo es útil un conjunto de trazas. Observe, en la figura 10.6_6, que la traza de la gráfica de z = senx en el plano xz es útil para construir la gráfica. Sin embargo, la traza en el plano xy es solo una serie de líneas paralelas, y la traza en el plano yz es simplemente una línea.

Las superficies cilíndricas están formadas por un conjunto de líneas paralelas. Sin embargo, no todas las superficies en tres dimensiones se construyen de manera tan simple. Ahora exploramos superficies más complejas, y los rastros son una herramienta importante en esta investigación.