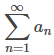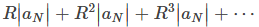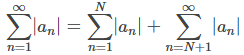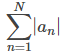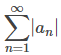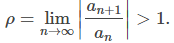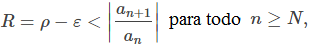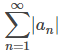| 7. Sucesiones y series infinitas | Ejercicios propuestos para el Capítulo 7.6 |

7.6 Pruebas de la razón y de la raíz

Objetivos de aprendizaje:

7.6.1. Usar la prueba de razón para determinar la convergencia absoluta de una serie.
7.6.2. Usar la prueba raíz para determinar la convergencia absoluta de una serie.
7.6.3. Describir una estrategia para probar la convergencia de una serie dada.

En esta sección, mostramos las últimas dos pruebas de convergencia de series: la prueba de la razón y la prueba de raíz. Estas pruebas son particularmente buenas porque no requieren que encontremos una serie para comparar. La prueba de la razón será especialmente útil en la discusión de series de potencia en el próximo capítulo.

A lo largo de este capítulo, hemos visto que ninguna prueba de convergencia funciona para todas las series. Por lo tanto, al final de esta sección, discutimos una estrategia para elegir qué prueba de convergencia usar para una serie dada.

Prueba de la razón

Considere una serie

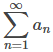
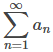
De nuestra discusión y ejemplos anteriores, sabemos que lim_{n → ∞} a_n = 0 no es una condición suficiente para que la serie converja. No solo necesitamos un a_n→ 0, sino que necesitamos un a_n→ 0 lo suficientemente rápido. Por ejemplo, considere la serie

y la serie

Sabemos que 1/n → 0 y 1/n² → 0. Sin embargo, solo la serie

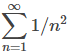
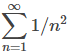
converge.

Las serie

diverge porque los términos en la secuencia {1/n} no se acercan a cero lo suficientemente rápido cuando n → ∞. Aquí presentamos la prueba de la razón, que proporciona una forma de medir qué tan rápido los términos de una serie se acercan a cero.

TEOREMA 7.6_1. Prueba de la razón

Sea

\[ \sum_{n=1}^{\infty} a_n \]

una serie dada con términos distintos de cero. Y sea

\[ \rho = \lim_{n \to \infty} \left| \frac{a_{n+1}}{a_n} \right| \]

i.    Si 0 ≤ ρ < 1, entonces la serie dada converge absolutamente.

ii.   Si ρ > 1 o ρ = ∞, entonces la serie dada diverge.

iii.  Si ρ = 1, la prueba no proporciona ninguna información.  ♦

Comprobación: Seauna serie con términos distintos de cero. Comenzamos con la prueba de la parte i. En este caso,En el intervalo 0 ≤ ρ <1, existe un R tal que 0 ≤ ρ < R < 1. Sea ε = R − ρ > 0. Por la definición de límite de una sucesión, existe algún número entero N tal quePor lo tanto,y por lo tanto,Para R < 1, la serie geométricaconverge Dadas las desigualdades anteriores, podemos aplicar la prueba de comparación y concluir que la serieconverge. Por lo tanto, desdedóndees una suma finita yconverge, concluimos queconverge. Para la parte ii.Para ρ > 1, existe un R tal que ρ > R > 1. Sea ε = ρ − R > 0. Por la definición del límite de una secuencia, existe un número entero N tal quePor lo tanto,y por lo tanto,Para R > 1, la serie geométricadiverge Aplicando la prueba de comparación, concluimos que la seriediverge, y por lo tanto la seriediverge. Para la parte iii. mostramos que la prueba no proporciona ninguna información si ρ = 1 al considerar la serie pPara cualquier número real p,Sin embargo, sabemos que si p ≤ 1, la serie pdiverge, mientras queconverge si p > 1.  ♦

EJEMPLO ILUSTRATIVO 7.6_1. Usando la prueba de la razón

Para cada una de las siguientes series, use la prueba de la razón para determinar si la serie converge o diverge.

Solución:
a. De la prueba de razón, podemos ver que

Ya que (n + 1)! = (n + 1) ⋅n !,

Para ρ < 1, la serie converge.

b. Podemos ver que

Para ρ > 1, la serie diverge.

c. Ya que

Observamos que

Para ρ < 1, la serie converge. ♦

Ejercicio de control 7.6.1

Use la prueba de la razón para determinar si la serie \( \sum_{n=1}^{\infty} \frac{n^3}{3^n} \) converge o diverge. ♦

Prueba de la raíz

El enfoque de la prueba de la raíz es similar al de la prueba de la razón. Considere una serie infinitatal quepara algún número real ρ. Entonces para N suficientemente grande, Por lo tanto, podemos aproximarnos a

escribiendoLa expresión en el lado derecho es una serie geométrica. Como en la prueba de razón, la serieconverge absolutamente si 0 ≤ ρ < 1 y la serie diverge si ρ ≥ 1. Si ρ = 1, la prueba no proporciona ninguna información. Por ejemplo, para cualquier serie p,

vemos que

Para evaluar este límite, utilizamos la función logaritmo natural. Al hacerlo, vemos que

Usando la regla de L’Hôpital, se deduce que lnρ = 0, y por lo tanto ρ = 1 para todo p. Sin embargo, sabemos que la serie p solo converge si p > 1 y diverge si p < 1.

TEOREMA 7.6_2. Prueba de la raíz

Considere la serie infinita dadaSea

\[ \rho = \lim_{n \to \infty} \sqrt[n]{|a_n|} \]

i.    Si 0 ≤ ρ <1, entonces la serie infinita converge absolutamente.

ii.   Si ρ > 1 o ρ = ∞, entonces la serie diverge.

iii.  Si ρ = 1, la prueba no proporciona ninguna información. ♦

       La prueba raíz es útil para series cuyos términos involucran exponenciales. En particular, para una serie cuyos términos satisfacen

entonces

y solo necesitamos evaluar lim_{n → ∞} b_n.

EJEMPLO ILUSTRATIVO 7.6_2. Usando la prueba de la raíz

Para cada una de las siguientes series, use la prueba de la raíz para determinar si la serie converge o diverge.

Solución:
a. Para aplicar la prueba de la raíz, calculamos

Dado que ρ < 1, la serie converge absolutamente.
b. Tenemos

(se aplicó la regla de L’Hôpital.)

Como ρ = ∞, la serie diverge. ♦

Ejercicio de control 7.6.2

Usa la prueba de la raíz para determinar si la serie \( \sum_{n=1}^{\infty} \frac{1}{n^n} \) converge o diverge. ♦

Elegir una prueba de convergencia

En este punto, tenemos una larga lista de pruebas de convergencia. Sin embargo, no todas las pruebas se pueden usar para todas las series. Cuando se nos da una serie, debemos determinar qué prueba es la mejor para usar. Aquí hay una estrategia para encontrar la mejor prueba para aplicar.

ESTRATEGIA PARA RESOLVER PROBLEMAS: ELEGIR UNA PRUEBA DE CONVERGENCIA PARA UNA SERIE

Considere una serie infinita En los pasos a continuación, describimos una estrategia para determinar si la serie converge. ¿Es la serie infinita una serie familiar? Por ejemplo, ¿es la serie armónica (que diverge) o la serie armónica alternante (que converge)? ¿Es una serie p o una serie geométrica? Si es así, verifique la potencia p o la razón r para determinar si la serie converge. ¿Es una serie alternante? ¿Nos interesa la convergencia absoluta o solo la convergencia? Si solo nos interesa saber si la serie converge, aplique la prueba de series alternantes. Si estamos interesados en la convergencia absoluta, proceda al paso 3, considerando la serie de valores absolutos. ¿Es la serie similar a una serie p o una serie geométrica? Si es así, pruebe la prueba de comparación o la prueba de comparación de límites. ¿Los términos de la serie contienen un factorial o potencia? Si los términos son potencias tales que , intente primero la prueba de la raíz. De lo contrario, intente la prueba de la razón primero. Usa la prueba de divergencia. Si esta prueba no proporciona ninguna información, intente la prueba de la integral.

Ejemplo ilustrativo 7.6.3.  Uso de pruebas de convergencia

Para cada una de las siguientes series, determina cuál prueba de convergencia es la mejor para usar y explica por qué. Luego determina si la serie converge o diverge. Si la serie es una serie alternada, determina si converge absolutamente, converge condicionalmente o diverge.

1. \( \sum_{n=1}^{\infty} \frac{n^2 + 2n}{n^3 + 3n^2 + 1} \)
2. \( \sum_{n=1}^{\infty} (-1)^{n+1} \frac{3n + 1}{n!} \)
3. \( \sum_{n=1}^{\infty} \frac{e^n}{n^3} \)
4. \( \sum_{n=1}^{\infty} \frac{3^n (n+1)}{n^n} \)

Solución:

1. Paso 1: La serie no es una serie \( p \)-serie ni una serie geométrica.

   Paso 2: La serie no es alternada.

   Paso 3: Para valores grandes de \( n \), aproximamos la serie con la expresión: \[ \frac{n^2 + 2n}{n^3 + 3n^2 + 1} \approx \frac{n^2}{n^3} = \frac{1}{n}. \]

   Por lo tanto, parece razonable aplicar la prueba de comparación o la prueba de comparación por el límite usando la serie \( \sum_{n=1}^{\infty} \frac{1}{n} \). Usando la prueba de comparación por el límite, vemos que: \[ \lim_{n \to \infty} \frac{\frac{n^2 + 2n}{n^3 + 3n^2 + 1}}{\frac{1}{n}} = \lim_{n \to \infty} \frac{n^3 + 2n^2}{n^3 + 3n^2 + 1} = 1. \]

   Dado que la serie \( \sum_{n=1}^{\infty} \frac{1}{n} \) diverge, esta serie también diverge.

2. Paso 1: La serie no es una serie conocida.

   Paso 2: La serie es alternada. Dado que estamos interesados en la convergencia absoluta, consideremos la serie: \[ \sum_{n=1}^{\infty} \frac{3n}{(n+1)!}. \]

   Paso 3: La serie no es similar a una \( p \)-serie ni a una serie geométrica.

   Paso 4: Dado que cada término contiene un factorial, aplicamos la prueba de la razón. Vemos que: \[ \lim_{n \to \infty} \frac{\frac{3(n+1)}{(n+1)!}}{\frac{3n}{n!}} = \lim_{n \to \infty} \frac{3n + 3}{(n+1)(3n + 1)} = 0. \]

   Por lo tanto, esta serie converge, y concluimos que la serie original converge absolutamente, y por ende converge.

3. Paso 1: La serie no es una serie conocida.

   Paso 2: No es una serie alternada.

   Paso 3: No hay una serie obvia con la cual comparar esta serie.

   Paso 4: No hay factorial. Hay una potencia, pero no es una situación ideal para la prueba de la raíz.

   Paso 5: Para aplicar la prueba de divergencia, calculamos: \[ \lim_{n \to \infty} \frac{e^n}{n^3} = \infty. \]

   Por lo tanto, por la prueba de divergencia, la serie diverge.

4. Paso 1: Esta serie no es una serie conocida.

   Paso 2: No es una serie alternada.

   Paso 3: No hay una serie obvia con la cual comparar esta serie.

   Paso 4: Dado que cada término es una potencia de \( n \), podemos aplicar la prueba de la raíz. Como: \[ \lim_{n \to \infty} \sqrt[n]{\frac{3^n (n+1)}{n^n}} = \lim_{n \to \infty} \frac{3n + 3}{n^n} = 0, \]

   por la prueba de la raíz, concluimos que la serie converge.

♦

Ejercicio de control 7.6.3

Para la serie \( \sum_{n=1}^{\infty} \frac{2n^3}{3^n + n} \), determine cuál es la mejor prueba de convergencia para usar y explica por qué. ♦

En la tabla siguiente, se resumen las pruebas de convergencia y cuándo pueden aplicarse. Nota que mientras las pruebas de comparación, comparación del límite e integral requieren que la serie \( \sum_{n=1}^{\infty} a_n \) tenga términos no negativos, si \( \sum_{n=1}^{\infty} a_n \) tiene términos negativos, estas pruebas pueden aplicarse a \( \sum_{n=1}^{\infty} |a_n| \) para verificar la convergencia absoluta.

Serie o prueba	Conclusiones	Comentarios
Prueba de divergencia \[ \sum_{n=1}^{\infty} a_n \]	\[ \text{Si } \lim_{n \to \infty} a_n \neq 0, \text{ la serie diverge} \]	Esta prueba no puede demostrar convergencia
Series geométricas \[ \sum_{n=1}^{\infty} ar^{n-1} \]	\[ \text{Si } |r| < 1, \text{ converge a } \frac{a}{1-r} \] \[ \text{Si } |r| \geq 1, \text{ diverge} \]	Aplicable a series geométricas
Series \(\mathit{p}\) \[ \sum_{n=1}^{\infty} \frac{1}{n^p} \]	\[ \text{Si } \mathit{p} > 1, \text{ converge} \] \[ \text{Si } \mathit{p} \leq 1, \text{ diverge} \]	Para \(\mathit{p} = 1\), tenemos la serie armónica
Prueba de comparación Para \(\sum_{n=1}^{\infty} a_n\) y \(\sum_{n=1}^{\infty} b_n\)	\[ \text{Si } a_n \leq b_n \text{ y } \sum b_n \text{ converge,} \] \[ \text{entonces } \sum a_n \text{ converge} \] \[ \text{Si } a_n \geq b_n \text{ y } \sum b_n \text{ diverge,} \] \[ \text{entonces } \sum a_n \text{ diverge} \]	Usada para series similares a geométricas o \(\mathit{p}\)-series
Prueba de comparación límite	\[ \text{Si } \lim_{n \to \infty} \frac{a_n}{b_n} = L \text{ (con } L \neq 0 \text{ y } L \neq \infty), \] \[ \text{entonces } \sum a_n \text{ y } \sum b_n \text{ ambas} \] \[ \text{convergen o ambas divergen} \]	Similar a la prueba de comparación
Prueba integral Si \(f\) es positiva, continua y decreciente	\[ \int_N^{\infty} f(x)dx \text{ y } \sum_{n=1}^{\infty} a_n \] \[ \text{convergen o divergen juntas} \]	\(f(n)\) debe ser integrable
Series alternantes \[ \sum_{n=1}^{\infty} (-1)^n b_n \]	\[ \text{Si } b_{n+1} \leq b_n \text{ y } b_n \to 0, \] \[ \text{entonces la serie converge} \]	Solo aplica a series alternantes
Prueba de la razón \[ \rho = \lim_{n \to \infty} \left|\frac{a_{n+1}}{a_n}\right| \]	\[ \text{Si } 0 \leq \rho < 1, \text{ converge absolutamente} \] \[ \text{Si } \rho > 1, \text{ diverge} \] \[ \text{Si } \rho = 1, \text{ inconclusa} \]	Frecuentemente usada con factoriales o exponenciales
Prueba de la raíz \[ \rho = \lim_{n \to \infty} \sqrt[n]{|a_n|} \]	\[ \text{Si } 0 \leq \rho < 1, \text{ converge absolutamente} \] \[ \text{Si } \rho > 1, \text{ diverge} \] \[ \text{Si } \rho = 1, \text{ inconclusa} \]	Usada para series donde \(|a_n| = b_n^n\)