SECCIONES CÓNICAS: Objetivos de aprendizaje
8.5.1. Identificar la ecuación de una parábola en forma estándar (canónica) dados el foco y la directriz.
8.5.2. Identificar la ecuación de una elipse en forma estándar (canónica) con focos dados.
8.5.3. Identificar la ecuación de una hipérbola en forma estándar (canónica) con focos dados.
8.5.4. Reconocer una parábola, elipse o hipérbola por su valor de excentricidad.
8.5.5. Escribir la ecuación polar de una sección cónica con excentricidad e.
8.5.6. Identificar cuándo una ecuación general de segundo grado es una parábola, elipse o hipérbola.
Las secciones cónicas se han estudiado desde la época de los antiguos griegos, y se consideraban un concepto matemático importante. Ya en 320 a.C., matemáticos griegos como Menecmo, Apolonio, Arquímedes y posteriormente Hipatia estaban fascinados por estas curvas. Apolonio escribió un tratado completo de ocho volúmenes sobre secciones cónicas en el que, por ejemplo, pudo derivar un método específico para identificar una sección cónica mediante el uso de la geometría. Desde entonces, han surgido aplicaciones importantes de secciones cónicas (por ejemplo, en astronomía), y las propiedades de las secciones cónicas se utilizan en radiotelescopios, receptores de antenas parabólicas e incluso en arquitectura. En esta sección discutimos las tres secciones cónicas básicas, algunas de sus propiedades y sus ecuaciones.
Las secciones cónicas reciben su nombre porque pueden generarse intersectando un plano con un cono. Un doble cono tiene dos partes idénticas llamadas hojas (Zill, Larson-Edwards). Se puede generar un cono circular recto girando una recta que pasa por el origen alrededor del eje y como se muestra en la figura 8.5_1.

Las secciones cónicas se generan por la intersección de un plano con un cono (Figura 8.5_2). Si el plano es paralelo al eje de revolución (el eje y), entonces la sección cónica es una hipérbola. Si el plano es paralelo a la recta generadora, la sección cónica es una parábola. Si el plano es perpendicular al eje de revolución, la sección cónica es una circunferencia. Si el plano intersecta una hoja (uno de los conos del doble cono) en ángulo con el eje (que no sea 90 °), entonces la sección cónica es una elipse.

Parábolas
Se genera una parábola cuando un plano intersecta un cono paralelo a la recta generadora. En este caso, el plano intersecta solo una de las hojas. Una parábola también se puede definir en términos de distancias.
Definición 8.2.1. La parábola
Una parábola es el conjunto de todos los puntos P(x, y) en el plano que son equidistantes de una recta fija L, llamada directriz y de un punto fijo F, ajeno a la directriz, llamado foco.
El vértice de la parábola es el punto medio entre el foco y la directriz.
El eje de la parábola es la recta que pasa por el foco y el vértice.
La parábola es simétrica respecto de su eje.
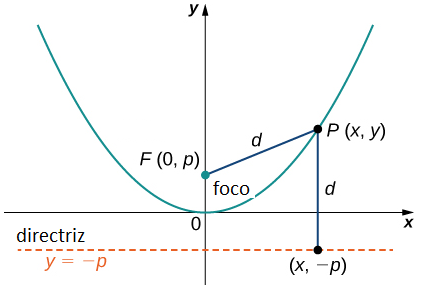
La gráfica de una parábola típica aparece en la figura 8.5_3. Usando este diagrama junto con la fórmula de la distancia, podemos deducir una ecuación para la parábola. Recordemos la fórmula de la distancia: dado el punto P con coordenadas (x₁, y₁) y el punto Q con coordenadas (x₂, y₂), la distancia entre ellos viene dada por la fórmula
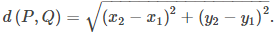
Luego, a partir de la definición de parábola y la Figura 8.5_3, obtenemos

Al cuadrar ambos miembros de la igualdad y simplificando, se obtiene
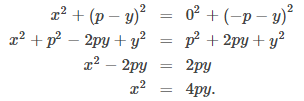
Ahora supongamos que queremos reubicar el vértice. Usamos las variables (h, k) para denotar las coordenadas del vértice. Entonces, si el foco está directamente sobre el vértice, tiene coordenadas (h, k + p) y la directriz tiene la ecuación y = k − p. De manera similar a como se dedujo la ecuación para el vértice en el origen se obtiene la fórmula (x − h)² = 4p (y − k). Resolver esta ecuación para y lleva al siguiente teorema.
TEOREMA 8.2.1. Ecuaciones para parábolas
Dada una parábola que abre hacia arriba con el vértice ubicado en (h, k) y el foco ubicado en (h, k + p), donde p es una constante, la ecuación para la parábola viene dada por

Esta es la forma estándar de una parábola.
También podemos estudiar los casos en que la parábola abre hacia abajo o hacia la izquierda o hacia la derecha. La ecuación para cada uno de estos casos también se puede escribir en forma estándar como se muestra en las siguientes gráficas:
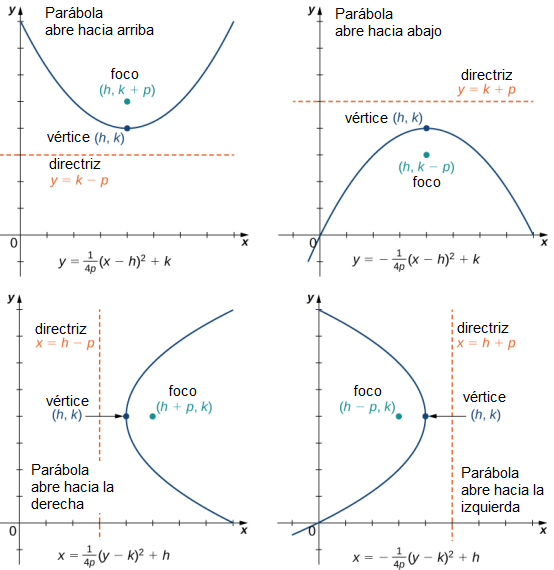
Además, la ecuación de una parábola se puede escribir en forma general, aunque en esta forma los valores de h, k y p no son reconocibles de inmediato. La forma general de una parábola se escribe como

La primera ecuación representa una parábola que abre hacia arriba o hacia abajo. La segunda ecuación representa una parábola que abre hacia la izquierda o hacia la derecha. Para poner la ecuación en forma estándar, use el método de completar el cuadrado.
Ejemplo ilustrativo
Escriba la ecuación 2y² − x + 12y + 16 = 0 en forma estándar y grafique la parábola resultante.
Solución – Juan Beltrán:

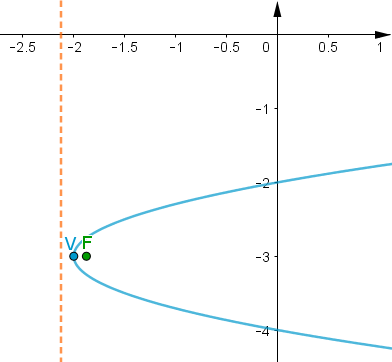
El eje de simetría de una parábola vertical (que abra hacia arriba o hacia abajo) es una recta vertical que pasa por el vértice. La parábola tiene una propiedad reflexiva interesante. Supongamos que tenemos una antena parabólica con una sección transversal parabólica. Si un haz de ondas electromagnéticas, como la luz o las ondas de radio, ingresa al plato en línea recta desde un satélite (paralelo al eje de simetría), entonces las ondas se reflejan en el plato y se acumulan en el foco de la parábola como se muestra en la siguiente figura.
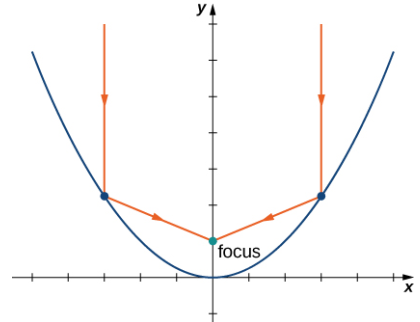
Considere un plato parabólico diseñado para recoger señales de un satélite en el espacio. El plato está dirigido directamente al satélite, y un receptor está ubicado en el foco de la parábola. Las ondas de radio procedentes del satélite se reflejan desde la superficie de la parábola hasta el receptor, que recoge y decodifica las señales digitales. Esto permite que un receptor pequeño recopile señales desde un gran ángulo de cielo. Las linternas y los faros de un automóvil funcionan con el mismo principio, pero a la inversa: la fuente de la luz (es decir, la bombilla) se encuentra en el foco y la superficie reflectante en el espejo parabólico enfoca el haz en línea recta. Esto permite que una pequeña bombilla ilumine un amplio ángulo de espacio frente a la linterna o el automóvil.
Ejercicios resueltos
Strang 7.5_258 Determine la ecuación de la parábola con foco F(2, 3); y directriz x = -2.
