APROXIMACIONES LINEALES Y DIFERENCIALES : Objetivos de aprendizaje
4.2.1 Describir la aproximación lineal a una función en un punto.
4.2.2 Escribir la linealización de una función dada.
4.2.3 Dibujar una gráfica que ilustre el uso de diferenciales para aproximar el cambio en una cantidad.
4.2.4 Calcular el error relativo y el error porcentual al usar una aproximación diferencial.
Acabamos de ver cómo las derivadas nos permiten comparar cantidades relacionadas que están cambiando con el tiempo. En esta sección, examinamos otra aplicación de las derivadas: la capacidad de aproximar funciones localmente mediante funciones lineales. Las funciones lineales son las funciones más fáciles con las que trabajar, por lo que proporcionan una herramienta útil para aproximar valores de funciones. Además, las ideas presentadas en esta sección se generalizan más adelante en el texto cuando estudiemos cómo aproximar funciones mediante polinomios y mediante series de potencias.
Aproximación lineal de una función en un punto
Considere una función f que es diferenciable en un punto x = a. Tenga presente que la recta tangente a la gráfica de f en a está dada por la ecuación
y = f (a) + f ‘(a) (x − a).
Por ejemplo, considere la función f (x) = 1/x en a = 2. Como f es diferenciable en x = 2 y f ‘(x) = – 1/x², vemos que f ‘ 2) = – 1/4. Por lo tanto, la recta tangente a la gráfica de f en a = 2 viene dada por la ecuación


La figura 4.2_1 (a) muestra una gráfica de f (x) = 1/x junto con la línea tangente a f en x = 2. Tenga en cuenta que para x cerca de 2, la gráfica de la recta tangente está cerca de la gráfica de f. Como resultado, podemos usar la ecuación de la recta tangente para aproximar f (x) para x cerca de 2. Por ejemplo, si x = 2.1, el valor y del punto correspondiente en la recta tangente es


El valor real de f (2.1) viene dado por


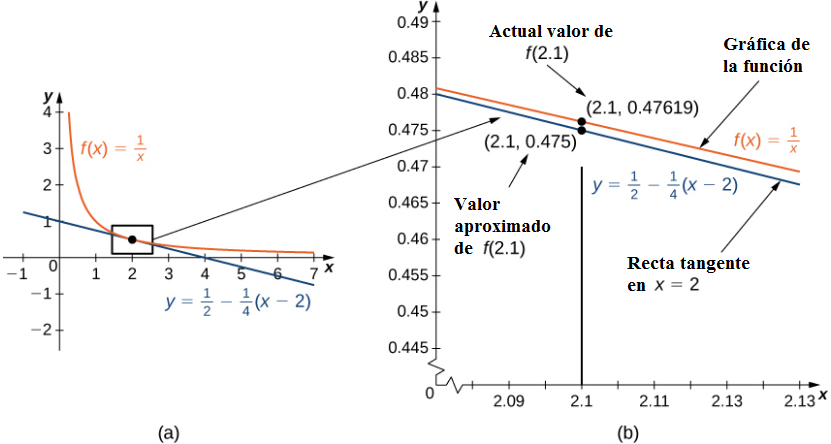

Por lo tanto, la recta tangente nos da una aproximación bastante buena de f (2.1) (Figura 4.2_1 (b)). Sin embargo, tenga en cuenta que para valores de x lejos de 2, la ecuación de la recta tangente no nos da una buena aproximación. Por ejemplo, si x = 10, el valor y del punto correspondiente en la recta tangente es


mientras que el valor real de la función en x = 10 es f (10) = 0.1.
En general, para una función diferenciable f, la ecuación de la recta tangente a f en x = a puede usarse para aproximar f (x) para x cerca de a. Por lo tanto, podemos escribir
f (x) ≈ f (a) + f ‘(a) (x − a),
para x cerca de a.
Definición 4.2.1. Aproximación lineal de una función en un punto
Llamamos a la función lineal
| L (x) = f (a) + f ′(a) (x − a) | (4.1) |
|
la aproximación lineal, o aproximación de recta tangente, de f en x = a. Esta función L también se conoce como la linealización de f en x = a. |
|
Para mostrar cuán útil puede ser la aproximación lineal, veamos cómo encontrar la aproximación lineal para f (x) = √x en x = 9.
EJEMPLO ILUSTRATIVO 4.2_1. Aproximación lineal de √x
Encuentre la aproximación lineal de f (x) = √x en x = 9 y use la aproximación para estimar √9.1.
Solución:
Como estamos buscando la aproximación lineal en x = 9, usando la ecuación 4.1 sabemos que la aproximación lineal viene dada por


Necesitamos encontrar f (9) y f ′(9).


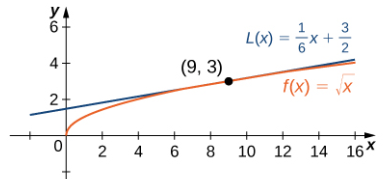
Por lo tanto, la aproximación lineal viene dada por la figura 4.2_2.


Usando la aproximación lineal, podemos estimar √9.1 escribiendo



Análisis
Usando una calculadora, el valor de √9.1 a cuatro decimales es 3.0166. El valor dado por la aproximación lineal, 3.0167, está muy cerca del valor obtenido con una calculadora, por lo que parece que usar esta aproximación lineal es una buena manera de estimar √x, al menos para x cerca de 9. Al mismo tiempo, puede parecer extraño usar una aproximación lineal cuando solo podemos presionar algunos botones en una calculadora para evaluar √.9.1. Sin embargo, ¿cómo evalúa la calculadora √9.1? ¡La calculadora usa una aproximación! De hecho, las calculadoras y las computadoras usan aproximaciones todo el tiempo para evaluar expresiones matemáticas; solo usan aproximaciones de mayor grado.
EJEMPLO ILUSTRATIVO 4.2_2. Aproximación lineal de sen x
Encuentre la aproximación lineal de f (x) = senx en x = π/3 y úsela para aproximar sen(62°).
Solución:
Primero notamos que dado que π/3 rad es equivalente a 60°, parece razonable usar la aproximación lineal en x = π/3. La aproximación lineal viene dada por


Observamos que


Por lo tanto, la aproximación lineal de f en x = π/3 viene dada por la figura 4.2_3.


Para estimar sen(62°) usando L, primero debemos convertir 62° a radianes. Tenemos que 62° = 62π/180 radianes, por lo que la estimación de sen(62°) viene dada por




Aproximaciones lineales para estimar raíces y potencias
Las aproximaciones lineales pueden usarse para estimar raíces y potencias. La aproximación lineal para f (x) = (1 + x)ⁿ en x = 0, puede usarse para estimar raíces y potencias para números reales cercanos a 1. La misma idea puede extenderse a un función de la forma f (x) = (m + x)ⁿ para estimar raíces y potencias cerca de un número diferente m.
EJEMPLO ILUSTRATIVO 4.2_3. Raíces y potencias aproximadas
Encuentre la aproximación lineal de f (x) = (1 + x)ⁿ en x = 0. Use esta aproximación para estimar (1.01)³.
Solución:
La aproximación lineal en x = 0 viene dada por


Porque


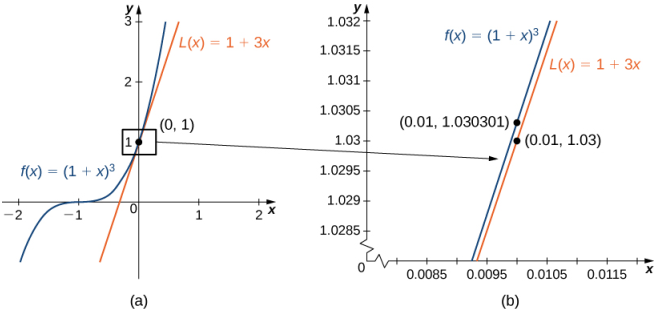
La aproximación lineal viene dada por la figura 4.2_4 (a).


Podemos aproximar (1.01)³ evaluando L(0.01) cuando n = 3. Concluimos que




Muchas gracias por la información, me ha sido de gran utilidad.
Muy bien! 👍