| 9. Ecuaciones diferenciales | 9.10. Sistemas lineales de ecuaciones diferenciales | Ejercicios propuestos para el Capítulo 9.10.4 |

9.10.4 Sistemas homogéneos con coeficientes constantes I

Ahora comenzaremos nuestro estudio del sistema homogéneo

y′ = Ay,         (9.10.4.1)

donde A es una matriz constante n × n. Como A es continua en (−∞, ∞), el Teorema 9.10.2.1 implica que todas las soluciones de (9.10.4.1) están definidas en (−∞, ∞). Por lo tanto, cuando hablamos de soluciones de y′ = Ay, nos referiremos a soluciones en (−∞, ∞).

      En esta sección suponemos que todos los valores propios de A son reales y que A tiene un conjunto de n vectores propios linealmente independientes. En las siguientes dos secciones consideraremos los casos donde algunos de los valores propios de A son complejos, o donde A no tiene n vectores propios linealmente independientes.

      En el Ejemplo 9.10.3.2 mostramos que las funciones vectoriales

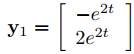  y 

forman un conjunto fundamental de soluciones del sistema

        (9.10.4.2)

pero no mostramos cómo obtuvimos y₁ e y₂ en primer lugar. Para ver cómo se pueden obtener estas soluciones escribimos (9.10.4.2) como

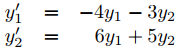        (9.10.4.3)

y buscar soluciones de la forma

y₁ = x₁e^λt  y  y₂ = x₂e^λt,         (9.10.4.4)

donde x₁, x₂ y λ son constantes por determinar. Diferenciando (9.10.4.4), obtenemos

y₁′ = λx₁e^λt  y  y₂′ = λx₂e^λt.

Sustituyendo esto y (9.10.4.4) en (9.10.4.3) y cancelando el factor común e^λt, se obtiene

Para un λ dado, este es un sistema algebraico homogéneo, ya que se puede reescribir como

        (9.10.4.5)

La solución trivial x₁ = x₂ = 0 de este sistema no es útil, ya que corresponde a la solución trivial y₁ ≡ y₂ ≡ 0 de (9.10.4.3), que no puede formar parte de un conjunto fundamental de soluciones de (9.10 .4.2). Por lo tanto, consideramos solo aquellos valores de λ para los cuales (9.10.4.5) tiene soluciones no triviales. Estos son los valores de λ para los cuales el determinante de (9.10.4.5) es cero; esto es,

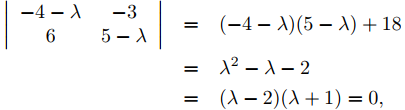
que tiene las soluciones λ₁ = 2 y λ₂ = −1.

      Tomando λ = 2 en (9.10.4.5), se obtiene

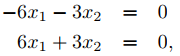
lo que implica que x₁ = −x₂/2, donde x₂ puede elegirse arbitrariamente. Elegir x₂ = 2 produce la solución y₁ = −e^2t, y₂ = 2e^2t de (9.10.4.3). Podemos escribir esta solución en forma vectorial como

        (9.10.4.6)

        Tomando λ = −1 en (9.10.4.5) se obtiene el sistema

entonces x₁ = −x₂. Tomando x₂ = 1 aquí se obtiene la solución y₁ = −e^−t, y₂ = e^−t de (9.10.4.3). Podemos escribir esta solución en forma vectorial como

        (9.10.4.7)

En (9.10.4.6) y (9.10.4.7) los coeficientes constantes en los argumentos de las funciones exponenciales son los valores propios de la matriz de coeficientes en (9.10.4.2), y los coeficientes vectoriales de las funciones exponenciales son vectores propios asociados. Esto ilustra el siguiente teorema.

Teorema 9.10.4.1

Supongamos que la matriz constante A de n×n tiene n valores propios reales λ₁, λ₂, . . ., λ_n (que no es necesario que sean distintos) con vectores propios asociados linealmente independientes x₁, x₂, . . ., x_n. Entonces las funciones

y₁ = x₁e^λ₁t, y₂ = x₂e^λ₂t, . . ., y_n = x_ne^λ_nt

forman un conjunto fundamental de soluciones de y′ = Ay; es decir, la solución general de este sistema es

y = c₁x₁e^λ₁t + c₂x₂e^λ₂t + · · · + c_nx_ne^λ_nt.  ♦

Prueba:

Derivando y_i = x_ie^λ_it y recordando que Ax_i = λ_ix_i se obtiene

y_i′ = λ_ix_ie^λ_it = Ax_ie^λ_it = Ay_i.

Esto muestra que y_i es una solución de y′ = Ay.  ♦

El wronskiano de {y₁, y₂, . . ., y_n} es

Como las columnas del determinante de la derecha son x₁, x₂, . . . , x_n, que se supone que son linealmente independientes, el determinante es distinto de cero. Por lo tanto, el Teorema 9.10.3.3 implica que {y₁, y₂, . . ., y_n} es un conjunto fundamental de soluciones de y′ = Ay.

Ejemplo ilustrativo 9.10.4.1

(a) Encuentre la solución general de

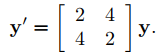         (9.10.4.8)

(b) Resuelva el problema de valor inicial

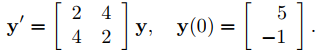        (9.10.4.9)

Solución:

(a) El polinomio característico de la matriz de coeficientes A en (9.10.4.8) es

Por lo tanto, λ₁ = 6 y λ₂ = −2 son valores propios de A. Para obtener los vectores propios, debemos resolver el sistema

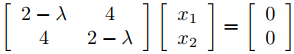        (9.10.4.10)

con λ = 6 y λ = −2. Al establecer λ = 6 en (9.10.4.10), se obtiene

lo que implica que x₁ = x₂. Tomando x₂ = 1 se obtiene el vector propio

entonces

es una solución de (9.10.4.8). Al establecer λ = −2 en (9.10.4.10) se obtiene

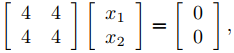
lo que implica que x₁ = −x₂. Tomando x₂ = 1 se obtiene el vector propio

entonces

es una solución de (9.10.4.8). Del Teorema 9.10.4.1, la solución general de (9.10.4.8) es

      (9.10.4.11)

(b) Para satisfacer la condición inicial en (9.10.4.9), debemos elegir c₁ y c₂ en (9.10.4.11) de modo que

Esto es equivalente al sistema

entonces c₁ = 2, c₂ = −3. Por lo tanto la solución de (9.10.4.9) es

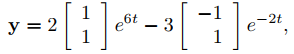
o, en términos de componentes,

y₁ = 2e^6t + 3e^−2t,  y₂ = 2e^6t − 3e^−2t.

Ejemplo ilustrativo 9.10.4.2

(a) Encuentre la solución general de

        (9.10.4.12)

(b) Resuelva el problema de valor inicial

      (9.10.4.13)

Solución:

(a) El polinomio característico de la matriz de coeficientes A en (9.10.4.12) es

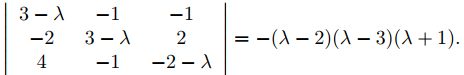
Por lo tanto, los valores propios de A son λ₁ = 2, λ₂ = 3 y λ₃ = −1. Para encontrar los vectores propios, debemos resolver el sistema

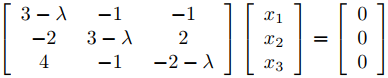        (9.10.4.14)

con λ = 2, 3, −1. Con λ = 2, la matriz aumentada de (9.10.4.14) es

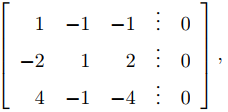
que es equivalente por filas a

Por lo tanto, x₁ = x₃ y x₂ = 0. Tomando x₃ = 1, se obtiene

como solución de (9.10.4.12). Con λ = 3, la matriz aumentada de (9.10.4.14) es

que es equivalente por filas a

Por lo tanto, x₁ = x₃ y x₂ = −x₃. Tomando x₃ = 1, se obtiene

como solución de (9.10.4.12). Con λ = −1, la matriz aumentada de (9.10.4.14) es

que es equivalente por filas a

Por lo tanto, x₁ = x₃/7 y x₂ = −3x₃/7. Tomando x3 = 7, obtenemos

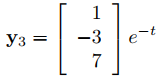
como solución de (9.10.4.12). Por el Teorema 9.10.4.1, la solución general de (9.10.4.12) es

que también se puede escribir como

      (9.10.4.15)

(b) Para satisfacer la condición inicial en (9.10.4.13) debemos elegir c₁, c₂, c₃ en (9.10.4.15) de modo que

Resolviendo este sistema se obtiene c₁ = 3, c₂ = −2, c₃ = 1. Por lo tanto, la solución de (9.10.4.13) es

♦

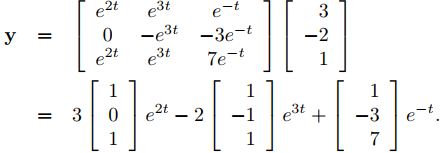Ejemplo ilustrativo 9.10.4.3

Encuentre la solución general de

        (9.10.4.16)

Solución:

El polinomio característico de la matriz de coeficientes A en (9.10.4.16) es

Por lo tanto, λ₁ = 1 es un valor propio de multiplicidad 1, mientras que λ₂ = −5 es un valor propio de multiplicidad 2.
Los vectores propios asociados con λ₁ = 1 son soluciones del sistema con matriz aumentada

que es equivalente por filas a

Por lo tanto, x₁ = x₂ = x₃, y elegimos x₃ = 1 para obtener la solución

        (9.10.4.17)

de (9.10.4.16). Los vectores propios asociados con λ₂ = −5 son soluciones del sistema con matriz aumentada

Por lo tanto, los componentes de estos vectores propios solo necesitan satisfacer la condición única

x₁ + x₂ + x₃ = 0.

Como aquí solo hay una ecuación, podemos elegir x₂ y x₃ arbitrariamente. Obtenemos un autovector eligiendo x₂ = 0 y x₃ = 1, y otro eligiendo x₂ = 1 y x₃ = 0. En ambos casos x₁ = −1.
Por lo tanto

son vectores propios linealmente independientes asociados con λ₂ = −5, y las soluciones correspondientes de (9.10.4.16) son

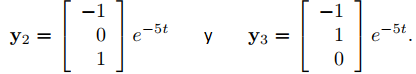
Por esto y (9.10.4.17), el teorema 9.10.4.1 implica que la solución general de (9.10.4.16) es

♦

Propiedades geométricas de soluciones cuando n = 2

Ahora consideraremos las propiedades geométricas de las soluciones de un sistema de coeficientes constantes de 2 × 2

        (9.10.4.18)

Es conveniente pensar en un “plano y₁–y₂“, donde un punto se identifica por coordenadas rectangulares (y₁, y₂).

Si 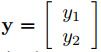es una solución no constante de (9.10.4.18), entonces el punto (y₁(t), y₂(t)) se mueve a lo largo de una curva C en el plano y₁–y₂ cuando t varía de −∞ a ∞. Llamamos a C la trayectoria de y. (También decimos que C es una trayectoria del sistema (9.10.4.18).) Es importante notar que C es la trayectoria de infinitas soluciones de (9.10.4.18), ya que si τ es cualquier número real, entonces y(t − τ) es una solución de (9.10.4.18) (Ejercicio 28(b)), y (y₁(t − τ), y₂(t − τ)) también se mueve a lo largo de C cuando t varía de −∞ a ∞. Además, el Ejercicio 28(c) implica que trayectorias distintas de (9.10.4.18) no pueden intersecarse, y que dos soluciones y₁ e y₂ de (9.10.4.18) tienen la misma trayectoria si y solo si y₂(t) = y₁(t − τ) para algún τ.

      Del Ejercicio 28(a), una trayectoria de una solución no trivial de (9.10.4.18) no puede contener (0, 0), que definimos como la trayectoria de la solución trivial y ≡ 0. Más generalmente, si 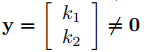es una solución constante de (9.10.4.18) (que podría ocurrir si cero es un valor propio de la matriz de (9.10.4.18)), definimos la trayectoria de y como el único punto ( k₁, k₂).

      Para ser específicos, esta es la pregunta: ¿Cómo se ven las trayectorias y cómo se recorren? En esta sección responderemos a esta pregunta, asumiendo que la matriz

de (9.10.4.18) tiene valores propios reales λ₁ y λ₂ con vectores propios asociados linealmente independientes x₁ y x₂. Entonces la solución general de (9.10.4.18) es

        (9.10.4.19)

Consideraremos otras situaciones en las próximas dos secciones.

        Le dejamos a usted (Ejercicio 35) clasificar las trayectorias de (9.10.4.18) si cero es un valor propio de A. Limitaremos nuestra atención aquí al caso donde ambos valores propios son distintos de cero. En este caso la situación más simple es donde λ₁ = λ₂ ≠ 0, entonces (9.10.4.19) se convierte en

y = (c₁x₁ + c₂x₂)e^λ1t.

Dado que x₁ y x₂ son linealmente independientes, un vector x arbitrario se puede escribir como x = c₁x₁ + c₂x₂. Por lo tanto, la solución general de (9.10.4.18) se puede escribir como y = xe^λ₁t donde x es un vector bidimensional arbitrario, y las trayectorias de las soluciones no triviales de (9.10.4.18) son semirrectas que pasan por (pero no incluyen) el origen . La dirección del movimiento se aleja del origen si λ₁ > 0 (Figura 9.10.4.1), hacia él si λ₁ < 0 (Figura 9.10.4.2). (En estas figuras y las siguientes, una flecha que pasa por un punto indica la dirección del movimiento a lo largo de la trayectoria que pasa por el punto).

Figura 9.10.4.1 Trayectorias de un sistema 2×2 con valor propio positivo repetido

Figura 9.10.4.2 Trayectorias de un sistema 2×2 con valor propio negativo repetido

Ahora suponga que λ₂ > λ₁, y sean L₁ y L₂ líneas que pasan por el origen paralelas a x₁ y x₂, respectivamente. Por media línea de L₁ (o L₂), nos referimos a cualquiera de los rayos obtenidos al eliminar el origen de L₁ (o L₂).

Haciendo c₂ = 0 en (10.4.19) se obtiene y = c₁x₁e^λ₁t. Si c₁ ≠ 0, la trayectoria definida por esta solución es una semirrecta de L₁. La dirección del movimiento se aleja del origen si λ₁ > 0, hacia el origen si λ₁ < 0.
De manera similar, la trayectoria de y = c₂x₂e^λ₂t con c₂ ≠ 0 es una semirrecta de L₂.

      De ahora en adelante, supondremos que c₁ y c₂ en (9.10.4.19) son ambos distintos de cero. En este caso, la trayectoria de (9.10.4.19) no puede intersecar L₁ o L₂, ya que cada punto en estas líneas está en la trayectoria de una solución para la cual c₁ = 0 o c₂ = 0. (Recuerde: trayectorias distintas no pueden cruzarse!). Por lo tanto, la trayectoria de (9.10.4.19) debe estar completamente en uno de los cuatro sectores abiertos delimitados por L₁ y L₂, pero no en ningún punto de L₁ o L₂. Desde el punto inicial (y₁(0), y₂(0)) definido por

y(0) = c₁x₁ + c₂x₂

está en la trayectoria, podemos determinar qué sector contiene la trayectoria a partir de los signos de c₁ y c₂, como se muestra en la Figura 9.10.4.3.

Figura 9.10.4.3 Cuatro sectores abiertos delimitados por L₁ y L₂

      La dirección de y(t) en (9.10.4.19) es la misma que la de

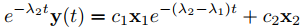        (9.10.4.20)

y de

       (9.10.4.21)

Como el lado derecho de (9.10.4.20) tiende a c₂x₂ cuando t → ∞, la trayectoria es asintóticamente paralela a L₂ cuando t → ∞. Como el lado derecho de (9.10.4.21) tiende a c₁x₁ cuando t → −∞, la trayectoria es asintóticamente paralela a L₁ cuando t → −∞.

       La forma y la dirección del recorrido de la trayectoria de (9.10.4.19) dependen de si λ₁ y λ₂ son positivos, negativos o de signos opuestos. Ahora analizaremos estos tres casos.
       En adelante, ||u|| denotará la longitud del vector u.

Caso 1: λ₂ > λ₁ > 0

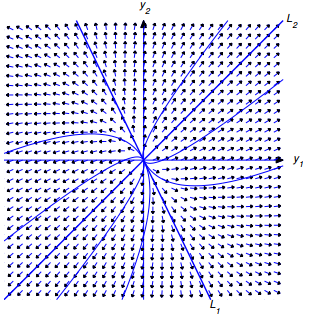
Figura 9.10.4.4 Dos valores propios positivos; movimiento lejos del origen

La Figura 9.10.4.4 muestra algunas trayectorias típicas. En este caso, lim_t→−∞ ||y(t)|| = 0, por lo que la trayectoria no solo es asintóticamente paralela a L₁ cuando t → −∞, sino que en realidad es asintóticamente tangente a L₁ en el origen. Por otro lado, lim_t→∞ ||y(t)|| = ∞ y

entonces, aunque la trayectoria es asintóticamente paralela a L₂ cuando t → ∞, no es asintóticamente tangente a L₂. La dirección del movimiento a lo largo de cada trayectoria se aleja del origen.

Caso 2: 0 > λ₂ > λ₁

Figura 9.10.4.5 Dos valores propios negativos; movimiento hacia el origen

La Figura 9.10.4.5 muestra algunas trayectorias típicas. En este caso, lim_t→∞ ||y(t)|| = 0, por lo que la trayectoria es asintóticamente tangente a L₂ en el origen cuando t → ∞. Por otro lado, lim_t→−∞ ||y(t)|| = ∞ y

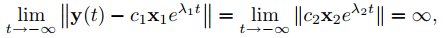
entonces, aunque la trayectoria es asintóticamente paralela a L₁ cuando t → −∞, no es asintóticamente tangente a ella. La dirección del movimiento a lo largo de cada trayectoria es hacia el origen.

Case 3: λ₂ > 0 > λ₁

Figura 9.10.4.6 Valores propios de diferentes signos

La Figura 9.10.4.6 muestra algunas trayectorias típicas. En este caso,

entonces la trayectoria es asintóticamente tangente a L₂ cuando t → ∞. Similarmente,

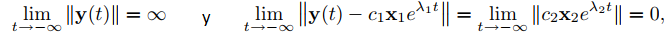
entonces la trayectoria es asintóticamente tangente a L₁ cuando t → −∞. La dirección del movimiento es hacia el origen en L₁ y lejos del origen en L₂. La dirección del movimiento a lo largo de cualquier otra trayectoria se aleja de L₁, hacia L₂.