| 9. Ecuaciones diferenciales | 9.3. Métodos numéricos |
9.3.2. El método de Euler mejorado y métodos relacionados
En la Sección 9.3.1 vimos que el error de truncamiento global del método de Euler es O(h), lo que parecería implicar que podemos lograr resultados arbitrariamente precisos con el método de Euler simplemente eligiendo un tamaño de paso lo suficientemente pequeño. Sin embargo, esto no es una buena idea, por dos razones. Primero, después de cierto punto, la reducción del tamaño del paso aumentará los errores de redondeo hasta el punto en que la precisión se deteriorará en lugar de mejorar. La segunda y más importante razón es que en la mayoría de las aplicaciones de métodos numéricos a un problema de valor inicial
y′ = f(x, y), y(x0) = y0, (9.3.2.1)
la parte costosa del cálculo es la evaluación de f. Por lo tanto, queremos métodos que den buenos resultados para un número determinado de tales evaluaciones. Esto es lo que nos motiva a buscar mejores métodos numéricos que el de Euler.
Para aclarar este punto, supongamos que queremos aproximar el valor de e aplicando el método de Euler al problema de valor inicial
y′ = y, y(0) = 1, (con solución y = ex)
en [0, 1], con h = 1/12, 1/24 y 1/48, respectivamente. Dado que cada paso del método de Euler requiere una evaluación de f, el número de evaluaciones de f en cada uno de estos intentos es n = 12, 24 y 48, respectivamente. En cada caso aceptamos yn como una aproximación a e. La segunda columna de la Tabla 9.3.2.1 muestra los resultados. La primera columna de la tabla indica el número de evaluaciones de f requeridas para obtener la aproximación, y la última columna contiene el valor de e redondeado a diez cifras significativas.

En esta sección estudiaremos el método de Euler mejorado, que requiere dos evaluaciones de f en cada paso. Hemos usado este método con h = 1/6, 1/12 y 1/24. El número requerido de evaluaciones de f fueron 12, 24 y 48, como en las tres aplicaciones del método de Euler; sin embargo, puede ver en la tercera columna de la tabla 9.3.2.1 que la aproximación a e obtenida por el método de Euler mejorado con solo 12 evaluaciones de f es mejor que la aproximación obtenida por el método de Euler con 48 evaluaciones.
En la Sección 9.3.3 estudiaremos el método de Runge-Kutta, que requiere cuatro evaluaciones de f en cada paso. Hemos usado este método con h = 1/3, 1/6 y 1/12. El número requerido de evaluaciones de f fue nuevamente 12, 24 y 48, como en las tres aplicaciones del método de Euler y el método de Euler mejorado; sin embargo, puede ver en la cuarta columna de la tabla 9.3.2.1 que la aproximación a e obtenida por el método de Runge-Kutta con solo 12 evaluaciones de f es mejor que la aproximación obtenida por el método de Euler mejorado con 48 evaluaciones.
Método de Euler mejorado
El método de Euler mejorado para resolver el problema de valor inicial (9.3.2.1) se basa en aproximar la curva integral de (9.3.2.1) en (xi, y(xi)) por la recta que pasa por (xi, y(xi)) con pendiente


es decir, mi es el promedio de las pendientes de las tangentes a la curva integral en los extremos de [xi, xi+1]. La ecuación de la recta de aproximación es por lo tanto


Haciendo x = xi+1 = xi + h en (9.3.2.2) se obtiene
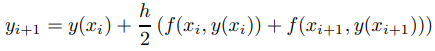
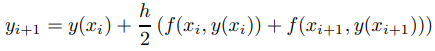
como una aproximación a y(xi+1). Como en nuestra derivación del método de Euler, reemplazamos y(xi) (desconocido si i > 0) por su valor aproximado yi; entonces (9.3.2.3) se convierte en


Sin embargo, esto seguirá sin funcionar porque no conocemos y(xi+1), que aparece a la derecha. Superamos esto reemplazando y(xi+1) por yi + hf(xi, yi), el valor que el método de Euler le asignaría a yi+1. Por lo tanto, el método de Euler mejorado comienza con el valor conocido y(x0) = y0 y calcula y1, y2, . . . , yn sucesivamente con la fórmula
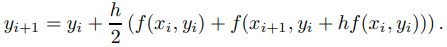
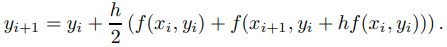
El cálculo indicado aquí se puede organizar convenientemente de la siguiente manera: dado yi, calcular


El método de Euler mejorado requiere dos evaluaciones de f(x, y) por paso, mientras que el método de Euler requiere solo una. Sin embargo, veremos al final de esta sección que si f satisface las suposiciones apropiadas, el error de truncamiento local con el método de Euler mejorado es O(h3), en lugar de O(h2) como con el método de Euler. Por lo tanto, el error de truncamiento global con el método de Euler mejorado es O(h2); sin embargo, no probaremos esto.
Observamos que la magnitud del error de truncamiento local en el método de Euler mejorado y otros métodos discutidos en esta sección está determinada por la tercera derivada y′′′ de la solución del problema de valor inicial. Por lo tanto, el error de truncamiento local será mayor donde |y′′′| es grande, o menor donde |y′′′| es pequeño.
El siguiente ejemplo, que trata del problema de valor inicial considerado en el Ejemplo 9.3.1.1, ilustra el procedimiento de cálculo indicado en el método de Euler mejorado.
Ejemplo ilustrativo 9.3.2.1
Use el método de Euler mejorado con h = 0.1 para encontrar valores aproximados de la solución del problema de valor inicial
y′ + 2y = x3e−2x, y(0) = 1 (9.3.2.5)
en x = 0,1, 0,2, 0,3.
Solución:
Como en el ejemplo 9.3.1.1, reescribimos (9.3.2.5) como
y′ = −2y + x3e−2x, y(0) = 1
que es de la forma (9.3.2.1), con
f(x, y) = −2y + x3e−2x, x0 = 0 y y0 = 1.
El método de Euler mejorado produce


Ejemplo ilustrativo 9.3.2.2
La tabla 9.3.2.2 muestra los resultados del uso del método de Euler mejorado con tamaños de paso h = 0,1 y h = 0,05 para encontrar valores aproximados de la solución del problema de valor inicial
y′ + 2y = x3e−2x, y(0) = 1
en x = 0, 0.1, 0.2, 0.3, . . . , 1.0. A modo de comparación, también muestra los valores aproximados correspondientes obtenidos con el método de Euler en el Ejemplo 9.3.1.2, y los valores de la solución exacta


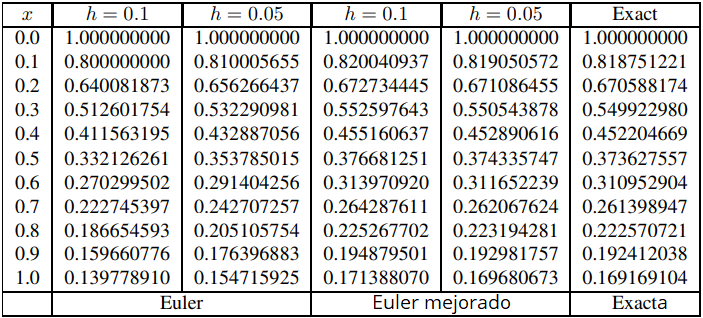

Los resultados obtenidos por el método de Euler mejorado con h = 0,1 son mejores que los obtenidos por el método de Euler con h = 0,05. ♦
Ejemplo ilustrativo 9.3.2.3
La tabla 9.3.2.3 muestra resultados análogos para el problema de valor inicial no lineal
y′ = −2y2 + xy + x2, y(0) = 1.
Aplicamos el método de Euler a este problema en el Ejemplo 9.3.1.3.
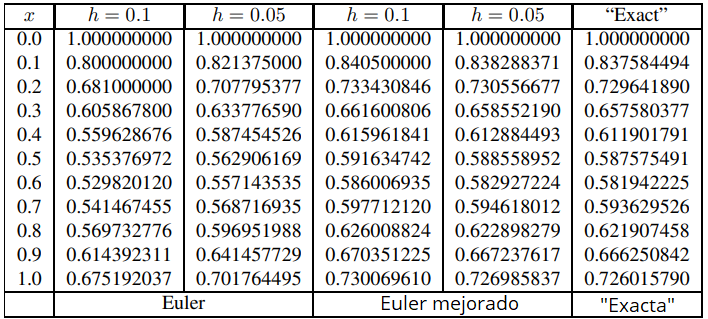

Ejemplo ilustrativo 9.3.2.4
Use tamaños de paso h = 0.2, h = 0.1 y h = 0.05 para encontrar valores aproximados de la solución de
y′ − 2xy = 1, y(0) = 3 (9.3.2.6)
en x = 0, 0,2, 0,4, 0,6, . . . , 2.0 por (a) el método de Euler mejorado; (b) el método semilineal de Euler mejorado. (Usamos el método de Euler y el método semilineal de Euler en este problema en el Ejemplo 9.3.1.4.)
Solución:
(a) Reescribiendo (9.3.2.6) como
y′ = 1 + 2xy, y(0) = 3
y aplicando el método de Euler mejorado con f(x, y) = 1 + 2xy se obtienen los resultados que se muestran en la Tabla 9.3.2.4.


(b) Dado que 

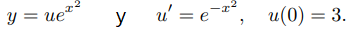
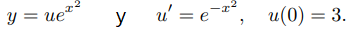
Los resultados enumerados en la Tabla 9.3.2.5 son claramente mejores que los obtenidos por el método de Euler mejorado.


Una familia de métodos con error de truncamiento local O(h3)
Ahora derivaremos una clase de métodos con error de truncamiento local O(h3) para resolver y′ = f(x, y), y(x0) = y0, (9.3.2.1). Para simplificar, asumimos que f, fx, fy, fxx, fyy y fxy son continuas y acotadas para todo (x, y). Esto implica que si y es la solución de (9.3.2.1), entonces y″ e y′′′ están acotados (Ejercicio 31).
Comenzamos aproximando la curva integral de (9.3.2.1) en (xi, y(xi)) por la recta que pasa por (xi, y(xi)) con pendiente
mi = σy′(xi) + ρy′(xi + θh),
donde σ, ρ y θ son constantes que pronto especificaremos; sin embargo, insistimos desde el principio en que 0 < θ ≤ 1, de modo que
xi < xi + θh ≤ xi+1.
La ecuación de la recta de aproximación es


Al establecer x = xi+1 = xi + h en (9.3.2.7) se obtiene


como una aproximación a y(xi+1).
Para determinar σ, ρ y θ de modo que el error
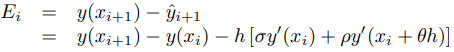
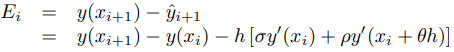
en esta aproximación es O(h3), comenzamos recordando del teorema de Taylor que


donde 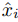
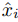
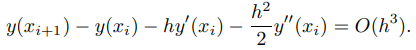
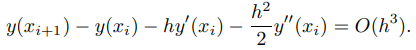
Comparando esto con (9.3.2.8) se muestra que Ei = O(h3) si


Sin embargo, la aplicación del teorema de Taylor a y′ muestra que


donde 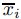
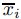
y′(xi + θh) = y′(xi) + θhy″(xi) + O(h2).
Sustituyendo esto en (9.3.2.9) y notando que la suma de dos términos O(h2) es nuevamente O(h2) muestra que Ei = O(h3) si


lo cual es cierto si
σ + ρ = 1 y ρθ = 1/2. (9.3.2.10)
Como y′ = f (x, y), ahora podemos concluir de (9.3.2.8) que


si σ, ρ y θ satisfacen (9.3.2.10). Sin embargo, esta fórmula no sería útil incluso si supiéramos exactamente el valor de y(xi) (como lo haríamos para i = 0), ya que aún no sabríamos exactamente el valor de y(xi + θh). Para superar esta dificultad, usamos de nuevo el teorema de Taylor para escribir


donde 



para alguna constante K. Como fy está acotada, el teorema del valor medio implica que


para alguna constante M. Dejando
u = y(xi + θh) y v = y(xi) + θhf (xi, y(xi))
y recordar (9.3.2.12) muestra que


Sustituyendo esto en (9.3.2.11) se obtiene
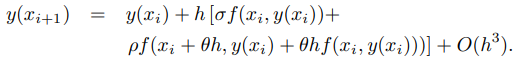
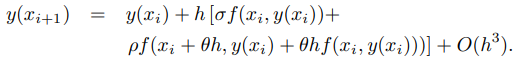
Esto implica que la fórmula


tiene un error de truncamiento local O(h3) si σ, ρ y θ satisfacen (9.3.2.10). Sustituyendo σ = 1 − ρ y θ = 1/2ρ aquí se obtiene


El cálculo indicado aquí se puede organizar convenientemente de la siguiente manera: dado yi, calcular


De acuerdo con nuestro requisito de que 0 < θ < 1, requerimos que ρ ≥ 1/2. Haciendo ρ = 1/2 in (9.3.2.13)
produce el método de Euler mejorado (9.3.2.4). Haciendo ρ = 3/4 se obtiene el método de Heun,
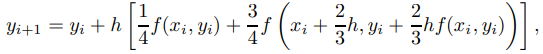
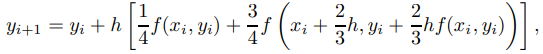
que se puede organizar como


Haciendo ρ = 1 se obtiene el método del punto medio,


que se puede organizar como


En los ejercicios 23 a 30 se dan ejemplos que involucran el método del punto medio y el método de Heun.
