Campos vectoriales

CAMPOS VECTORIALES: Objetivos de aprendizaje

10.12.1. Reconocer un campo vectorial en un plano o en el espacio.
10.12.2. Dibuja un campo vectorial a partir de una ecuación dada.
10.12.3. Identificar un campo conservador y su función potencial asociada.

Los campos vectoriales son una herramienta importante para describir muchos conceptos físicos, como la gravitación y el electromagnetismo, que afectan el comportamiento de los objetos en una gran región de un plano o del espacio. También son útiles para tratar comportamientos a gran escala, como tormentas atmosféricas o corrientes oceánicas de aguas profundas. En esta sección, examinamos las definiciones básicas y los gráficos de los campos vectoriales para poder estudiarlos con más detalle en el resto de este capítulo.

Ejemplos de campos vectoriales

¿Cómo podemos modelar la fuerza gravitacional ejercida por múltiples objetos astronómicos? ¿Cómo podemos modelar la velocidad de las partículas de agua en la superficie de un río? La figura 10.12_1 da representaciones visuales de tales fenómenos.

La figura 10.12_1 (a) muestra un campo gravitacional ejercido por dos objetos astronómicos, como una estrella y un planeta o un planeta y una luna. En cualquier punto de la figura, el vector asociado con un punto proporciona la fuerza gravitacional neta ejercida por los dos objetos sobre un objeto de unidad de masa. Los vectores de mayor magnitud en la figura son los vectores más cercanos al objeto más grande. El objeto más grande tiene mayor masa, por lo que ejerce una fuerza gravitacional de mayor magnitud que el objeto más pequeño.

La figura 10.12_1 (b) muestra la velocidad de un río en puntos de su superficie. El vector asociado con un punto dado en la superficie del río da la velocidad del agua en ese punto. Como los vectores a la izquierda de la figura son pequeños en magnitud, el agua fluye lentamente en esa parte de la superficie. A medida que el agua se mueve de izquierda a derecha, se encuentra con algunos rápidos alrededor de una roca. La velocidad del agua aumenta y se produce un remolino en parte de los rápidos.

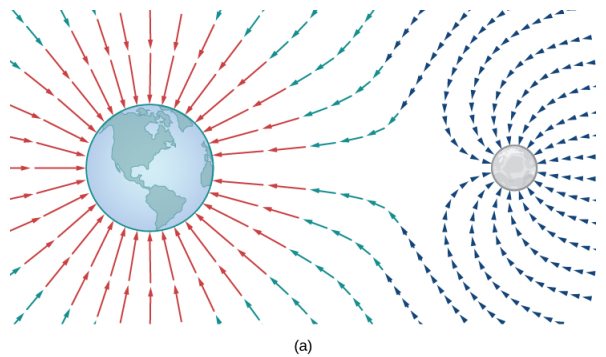
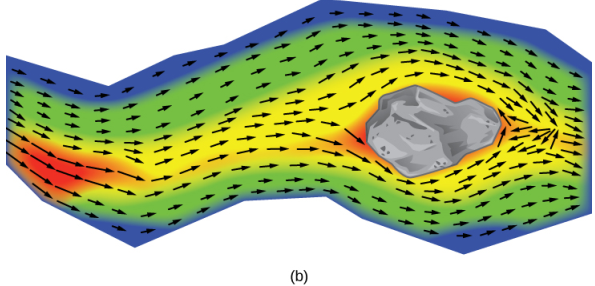
Figura 10.12_1 (a) El campo gravitacional ejercido por dos cuerpos astronómicos en un objeto pequeño. (b) El campo de velocidad del vector del agua en la superficie de un río muestra las variadas velocidades del agua. El rojo indica que la magnitud del vector es mayor, por lo que el agua fluye más rápidamente; azul indica una magnitud menor y una velocidad más lenta del flujo de agua.

Cada figura ilustra un ejemplo de un campo vectorial. Intuitivamente, un campo vectorial es un mapa de vectores. En esta sección, estudiamos campos vectoriales en R² y R³.

DEFINICIÓN. Campos vectoriales Un campo vectorial F en ℝ² es una asignación de un vector bidimensional F (x, y) a cada punto (x, y) de un subconjunto D de ℝ². El subconjunto D es el dominio del campo vectorial. Un campo vectorial F en ℝ³ es una asignación de un vector tridimensional F (x, y, z) a cada punto (x, y, z) de un subconjunto D de ℝ³. El subconjunto D es el dominio del campo vectorial.

Campos de vectores en ℝ²

Un campo vectorial en ℝ² se puede representar de dos formas equivalentes. La primera forma es usar un vector con componentes que son funciones de dos variables:

La segunda forma es usar los vectores unitarios estándar:

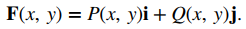
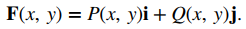
Se dice que un campo vectorial es continuo si sus funciones componentes son continuas.

EJEMPLO ILUSTRATIVO 10.12_1. Encontrar un vector asociado con un punto dado

Sea F(x, y) = (2y² + x − 4) i + cos (x) j un campo vectorial en R². Tenga en cuenta que este es un ejemplo de un campo vectorial continuo ya que ambas funciones componentes son continuas. ¿Qué vector está asociado con el punto (0, −1)?

Solución:

Sustituya los valores de puntos para x e y:

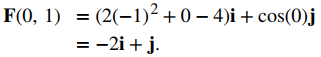
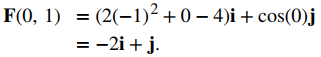
Dibujando un campo vectorial

Ahora podemos representar un campo vectorial en términos de sus componentes de funciones o vectores unitarios, pero representarlo visualmente al dibujarlo es más complejo porque el dominio de un campo vectorial está en R², al igual que el rango. Por lo tanto, el “gráfico” de un campo vectorial en R² vive en un espacio de cuatro dimensiones. Como no podemos representar visualmente el espacio de cuatro dimensiones, en su lugar dibujamos campos vectoriales de R² en un plano. Para hacer esto, dibuje el vector asociado con un punto dado en el punto en un plano. Por ejemplo, suponga que el vector asociado con el punto (4, −1) es ⟨3, 1⟩. Luego, dibujaríamos el vector ⟨3, 1⟩ en el punto (4, −1).
Deberíamos trazar suficientes vectores para ver la forma general, pero no tantos que el boceto se convierta en un caos desordenado. Si tuviéramos que trazar el vector de imagen en cada punto de la región, llenaría la región por completo y es inútil. En cambio, podemos elegir puntos en las intersecciones de las líneas de la cuadrícula y trazar una muestra de varios vectores de cada cuadrante de un sistema de coordenadas rectangular en R².
Hay dos tipos de campos vectoriales en R² en los que se centra este capítulo: campos radiales y campos rotacionales. Los campos radiales modelan ciertos campos gravitacionales y campos de fuente de energía, y los campos rotacionales modelan el movimiento de un fluido en un vórtice. En un campo radial, todos los vectores apuntan directamente hacia o directamente lejos del origen. Además, la magnitud de cualquier vector depende solo de su distancia desde el origen. En un campo radial, el vector ubicado en el punto (x, y) es perpendicular al círculo centrado en el origen que contiene el punto (x, y), y todos los demás vectores en este círculo tienen la misma magnitud.

EJEMPLO ILUSTRATIVO 10.12_2. Dibujar un campo vectorial radial

Dibuja el campo vectorial

Solución:
Para dibujar este campo vectorial, elija una muestra de puntos de cada cuadrante y calcule el vector correspondiente. La siguiente tabla ofrece una muestra representativa de puntos en un plano y los vectores correspondientes:

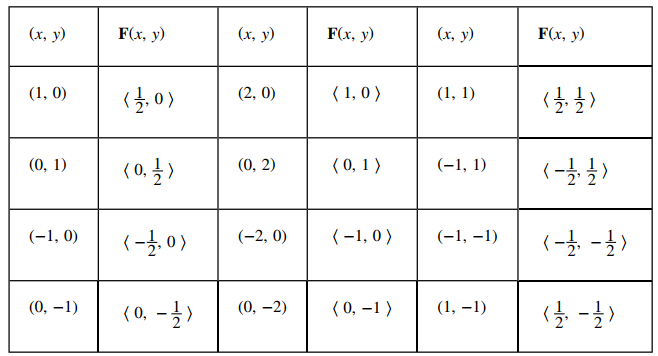
La figura 10.12_2 (a) muestra el campo vectorial. Para ver que cada vector es perpendicular al círculo correspondiente, la Figura 10.12_2 (b) muestra círculos superpuestos en el campo del vector.

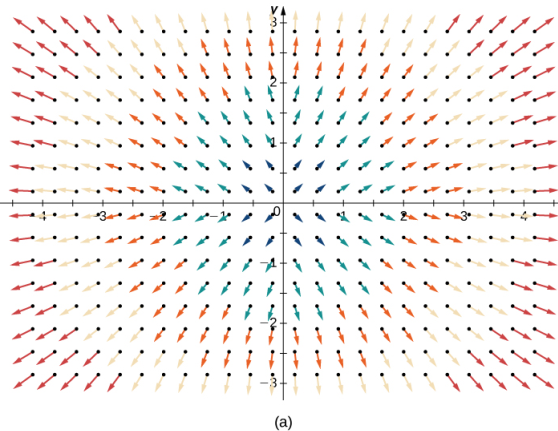
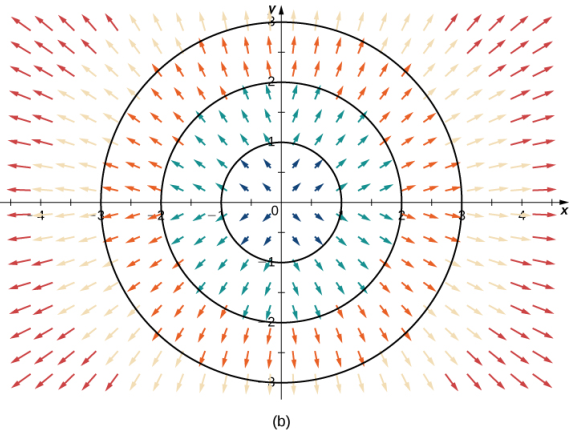
Figura 10.2_2 (a) Una representación visual del campo vectorial radial F(x, y) = (x/2) i + (y/2) j. (b) El campo vectorial radial F(x, y) = (x/2) i + (y/2) j con círculos superpuestos. Observe que cada vector es perpendicular al círculo en el que se encuentra.

A diferencia de los campos radiales, en un campo rotacional, el vector en el punto (x, y) es tangente (no perpendicular) a un círculo con radio r = √(x² + y²) . En un campo rotacional estándar, todos los vectores apuntan en sentido horario o en sentido antihorario, y la magnitud de un vector depende solo de su distancia desde el origen. Los dos ejemplos siguientes son campos de rotación en el sentido de las agujas del reloj, y vemos en sus representaciones visuales que los vectores parecen girar alrededor del origen.

EJEMPLO ILUSTRATIVO 10.12_3. Dibujar un campo vectorial rotacional

Dibuje el campo vectorial F(x, y) = ⟨y, −x⟩.

Solución:
Cree una tabla (vea la siguiente) usando una muestra representativa de puntos en un plano y sus vectores correspondientes. La figura 10.12_4 muestra el campo vectorial resultante.

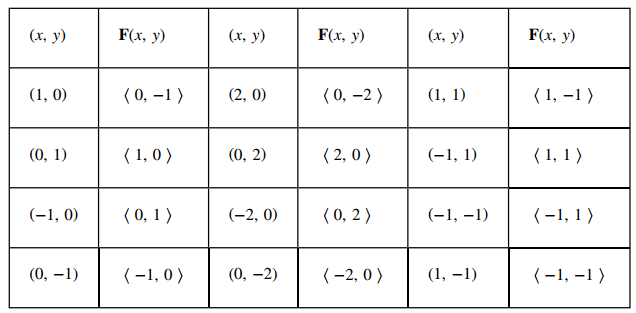
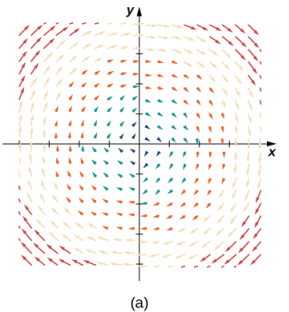
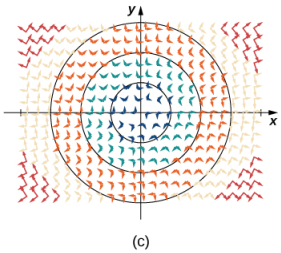
Figura 10.12_4 (a) Una representación visual del campo vectorial F(x, y) = ⟨y, −x⟩. (b) Campo vectorial F(x, y) = ⟨y, −x⟩ con círculos centrados en el origen. (c) El vector F(a, b) es perpendicular al vector radial ⟨a, b⟩ en el punto (a, b).

Análisis

Tenga en cuenta que el vector F(a, b) = ⟨b, −a⟩ apunta en sentido horario y es perpendicular al vector radial ⟨a, b⟩. (Podemos verificar esta afirmación calculando el producto escalar de los dos vectores: ⟨a, b⟩⋅⟨ − b, a⟩ = −ab + ab = 0.) Además, el vector ⟨b, −a⟩ tiene una longitud r = √(a² + b²). Por lo tanto, tenemos una descripción completa de este campo vectorial rotacional: el vector asociado con el punto (a, b) es el vector con longitud r tangente al círculo con radio r, y apunta en la dirección de las agujas del reloj.

Los bocetos mostrados en estas figuras a menudo se usan para analizar los principales sistemas de tormentas, incluidos huracanes y ciclones. En el hemisferio norte, las tormentas giran en sentido antihorario; En el hemisferio sur, las tormentas giran en sentido horario. (Este es un efecto causado por la rotación de la Tierra sobre su eje y se llama Efecto Coriolis).

EJEMPLO ILUSTRATIVO 10.12_4. Dibujar un campo vectorial

Dibuje el campo vectorial correspondiente a

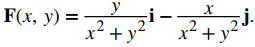
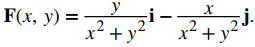
Solución:
Para visualizar este campo vectorial, primero tenga en cuenta que el producto de punto F(a, b) ⋅ (ai + bj) es cero para cualquier punto (a, b). Por lo tanto, cada vector es tangente al círculo en el que se encuentra. Además, como (a, b) → (0, 0), la magnitud de F(a, b) va al infinito. Para ver esto, tenga en cuenta que

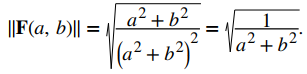
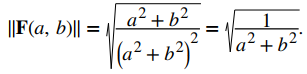
Como 1/(a² + b²) → ∞ cuando (a, b) → (0, 0), entonces || F(a, b) || → ∞ cuando (a, b) → (0, 0). Este campo vectorial es similar al campo vectorial del el ejemplo anterior, pero en este caso las magnitudes de los vectores cercanos al origen son grandes. La siguiente tabla muestra una muestra de puntos y los vectores correspondientes, y la Figura 10.12_5 muestra el campo vectorial. Tenga en cuenta que este campo vectorial modela el movimiento del remolino del río en la Figura 10.12_1 (b). El dominio de este campo vectorial es todo R² excepto el punto (0, 0).

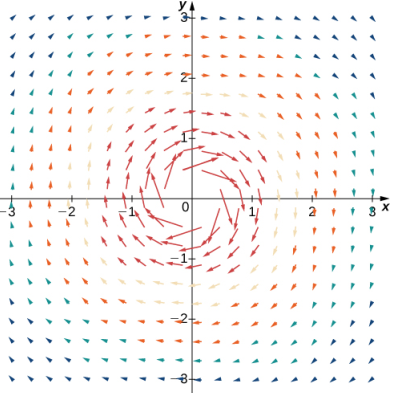
EJEMPLO ILUSTRATIVO 10.12_5. Campo de velocidad de un fluido

Suponer que

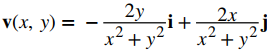
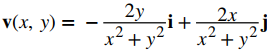
es el campo de velocidad de un fluido. ¿Qué tan rápido se mueve el fluido en el punto (1, −1)? (Suponga que las unidades de velocidad son metros por segundo).

Solución:
Para encontrar la velocidad del fluido en el punto (1, −1), sustituya las coordenadas del punto en v:

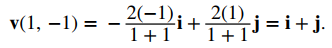
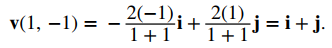
La velocidad del fluido en (1, −1) es la magnitud de este vector. Por lo tanto, la velocidad es || i + j || = √ 2 m / seg.

Hemos examinado campos vectoriales que contienen vectores de varias magnitudes, pero al igual que tenemos vectores unitarios, también podemos tener un campo vectorial unitario. Un campo vectorial F es un campo vectorial unitario si la magnitud de cada vector en el campo es 1. En un campo vectorial unitario, la única información relevante es la dirección de cada vector.

EJEMPLO ILUSTRATIVO 10.12_6. Un campo vectorial de unidad

Mostrar que el campo vectorial

es un campo vectorial unitario.

Solución:
Para mostrar que F es un campo unitario, debemos mostrar que la magnitud de cada vector es 1. Tenga en cuenta que

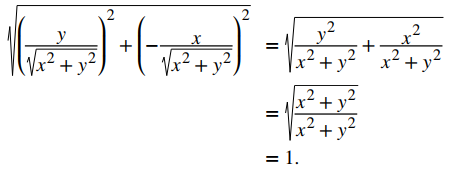
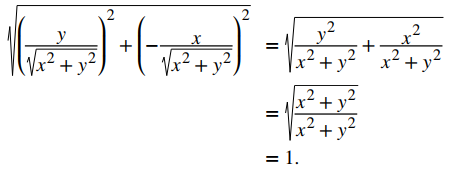
Por lo tanto, F es un campo vectorial unitario.

¿Por qué son importantes los campos vectoriales unitarios? Supongamos que estamos estudiando el flujo de un fluido, y solo nos importa la dirección en la que fluye el fluido en un punto dado. En este caso, la velocidad del fluido (que es la magnitud del vector de velocidad correspondiente) es irrelevante, porque lo único que nos importa es la dirección de cada vector. Por lo tanto, el campo del vector unitario asociado con la velocidad es el campo que estudiaríamos.

Si F = ⟨P, Q, R⟩ es un campo vectorial, entonces el campo vectorial de la unidad correspondiente es

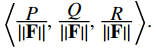
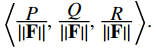
Observe que si F(x, y) = ⟨y, −x⟩ es el campo vectorial del Ejemplo 10.12_3, entonces la magnitud de F es √(x² + y²) y, por lo tanto, el campo del vector unitario correspondiente es el campo G del ejemplo anterior.

Si F es un campo vectorial, entonces el proceso de dividir F por su magnitud para formar un campo vectorial unitario F / || F || se llama normalizar el campo F.