| 9. Ecuaciones diferenciales | 9.13. Problemas de valores en la frontera para ecuaciones diferenciales ordinarias de segundo orden | 

9.13.2 PROBLEMAS DE STURM-LIOUVILLE

En esta sección consideramos problemas de valores propios de la forma

P₀(x)y′′ + P₁(x)y′ + P₂(x)y + λR(x)y = 0,  B₁(y) = 0, B₂(y) = 0,         (9.13.2.1)

donde

B₁(y) = αy(a) + βy′(a)  y  B₂(y) = ρy(b) + δy′(b).

Como en la Sección 9.13.1, α, β, ρ y δ son números reales, con

α² + β² > 0  y  ρ² + δ² > 0,

P₀, P₁, P₂ y R son continuos, y P₀ y R son positivos en [a, b].

      Decimos que λ es un valor propio de (9.13.2.1) si (9.13.2.1) tiene una solución no trivial y. En este caso, y es una función propia asociada con λ, o una función propia λ. Resolver el problema de los valores propios significa encontrar todos los valores propios y las funciones propias asociadas de (9.13.2.1).

Ejemplo ilustrativo 9.13.2.1

Resolver el problema de valor propio

y′′ + 3y′ + 2y + λy = 0,  y(0) = 0, y(1) = 0.         (9.13.2.2)

Solución:

La ecuación característica de (9.13.2.2) es

r² + 3r + 2 + λ = 0,

con ceros

  y 

Si λ < 1/4 entonces r₁ y r₂ son reales y distintos, por lo que la solución general de la ecuación diferencial en (9.13.2.2) es

Las condiciones de contorno requieren que

Dado que el determinante de este sistema es e^r₂ − e^r₁ ≠ 0, el sistema solo tiene la solución trivial. Por lo tanto, λ no es un valor propio de (9.13.2.2).

      Si λ = 1/4 entonces r₁ = r₂ = −3/2, entonces la solución general de (9.13.2.2) es

y = e^−3x/2(c₁ + c₂x).

La condición de frontera y(0) = 0 requiere que c₁ = 0, entonces y = c₂xe^−3x/2 y la condición de frontera y(1) = 0 requiere que c₂ = 0. Por lo tanto, λ = 1/4 no es un valor propio de ( 9.13.2.2).

      Si λ > 1/4 entonces

  y 

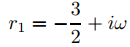
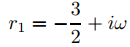
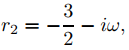
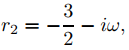
con

o equivalente,          (9.13.2.3)

En este caso, la solución general de la ecuación diferencial en (9.13.2.2) es

y = e^−3x/2(c₁ cosωx + c₂senωx).

La condición de contorno y(0) = 0 requiere que c₁ = 0, por lo que y = c₂e^−3x/2senωx, lo cual se cumple con c₂ ≠ 0 si y solo si ω = nπ, donde n es un número entero. Podemos suponer que n es un número entero positivo. (¿Por qué?). De (9.13.2.3), los valores propios son λn = (1 + 4n²π₂)/4, con funciones propias asociadas

y_n = e^−3x/2sennπx,  n = 1, 2, 3, . . .  .  ♦

Ejemplo ilustrativo 9.13.2.2

Resolver el problema de valor propio

x²y′′ + xy′ + λy = 0,  y(1) = 0, y(2) = 0.         (9.13.2.4)

Solución:

Si λ = 0, la ecuación diferencial en (9.13.2.4) se reduce a x(xy′)′ = 0, entonces xy′ = c₁,

y′ = c₁/x,  y  y = c₁lnx + c₂.

La condición de contorno y(1) = 0 requiere que c₂ = 0, por lo que y = c₁lnx. La condición de contorno y(2) = 0 requiere que c₁ln2 = 0, por lo que c₁ = 0. Por lo tanto, cero no es un valor propio de (9.13.2.4).

      Si λ < 0, escribimos λ = −k² con k > 0, entonces (9.13.2.4) se convierte en

x²y′′ + xy′ − k²y = 0,

una ecuación de Euler (Sección 9.7.4) con ecuación indicial

r² − k² = (r − k)(r + k) = 0.

Por lo tanto

y = c₁x^k + c₂x^−k.

Las condiciones de contorno requieren que

Como el determinante de este sistema es 2^−k − 2^k ≠ 0,  c₁ = c₂ = 0. Por lo tanto (9.13.2.4) no tiene valores propios negativos.

      Si λ > 0 escribimos λ = k² con k > 0. Entonces (9.13.2.4) se convierte en

x²y′′ + xy′ + k²y = 0,

una ecuación de Euler con ecuación indicial

r² + k² = (r − ik)(r + ik) = 0,

por lo que

y = c₁cos(klnx) + c₂sen(klnx).

La condición de frontera y(1) = 0 requiere que c₁ = 0. Por lo tanto, y = c₂sen(klnx). Esto se cumple con c₂ ≠ 0 si y solo si k = nπ/ln2, donde n es un entero positivo. Por lo tanto, los valores propios de (9.13.2.4) son λ_n = (nπ/ln 2)², con funciones propias asociadas

♦

      Para propósitos teóricos, es útil reescribir la ecuación diferencial en (9.13.2.1) en una forma diferente, proporcionada por el siguiente teorema.

Teorema 9.13.2.1

Si P₀, P₁, P₂ y R son continuos y P₀ y R son positivos en un intervalo cerrado [a, b], entonces la ecuación

P₀(x)y′′ + P₁(x)y′ + P₂(x)y + λR(x)y = 0         (9.13.2.5)

se puede reescribir como

(p(x)y′)′ + q(x)y + λr(x)y = 0,         (9.13.2.6)

donde p, p′, q y r son continuos y p y r son positivos en [a, b].  ♦

Prueba:

Comenzamos reescribiendo (9.13.2.5) como

y′′ + u(x)y′ + v(x)y + λR₁(x)y = 0,         (9.13.2.7)

con u = P₁/P₀, v = P₂/P₀ y R₁ = R/P₀. (Observe que R₁ es positivo en [a, b].) Ahora sea p(x) = e^U(x), donde U es cualquier antiderivada de u. Entonces p es positivo en [a, b] y, como U′ = u,

p′(x) = p(x)u(x)         (9.13.2.8)

es continua en [a, b]. Multiplicando (9.13.2.7) por p(x), se obtiene

p(x)y′′ + p(x)u(x)y′ + p(x)v(x)y + λp(x)R₁(x)y = 0.          (9.13.2.9)

Dado que p es positivo en [a, b], esta ecuación tiene las mismas soluciones que (9.13.2.5). De (9.13.2.8),

(p(x)y′)′ = p(x)y′′ + p′(x)y′ = p(x)y′′ + p(x)u(x)y′,

entonces (9.13.2.9) se puede reescribir como en (9.13.2.6), con q(x) = p(x)v(x) y r(x) = p(x)R₁(x). Esto completa la demostración. ♦

      Debe entenderse en el resto de esta sección que p, q y r tienen las propiedades establecidas en el Teorema 9.13.2.1. Además, cada vez que escribimos Ly en un enunciado general, queremos decir

Ly = (p(x)y′)′ + q(x)y.

      La ecuación diferencial (9.13.2.6) se denomina ecuación de Sturm-Liouville y el problema de valores propios

(p(x)y′)′ + q(x)y + λr(x)y = 0,  B₁(y) = 0, B₂(y) = 0,       (9.13.2.10)

que es equivalente a (9.13.2.1), se llama problema de Sturm-Liouville.

Ejemplo ilustrativo 9.13.2.3

Reescribir el problema de valor propio

y′′ + 3y′ + (2 + λ)y = 0,  y(0) = 0, y(1) = 0          (9.13.2.11)

del ejemplo 9.13.2.1 como un problema de Sturm-Liouville.

Solución:

La comparación de (9.13.2.11) con (9.13.2.7) muestra que u(x) = 3, por lo que tomamos U(x) = 3x y p(x) = e^3x. Multiplicando la ecuación diferencial en (9.13.2.11) por e^3x, se obtiene

e^3x(y′′ + 3y′) + 2e^3xy + λe^3xy = 0.

Ya que

e^3x(y′′ + 3y′) = (e^3xy′)′,

(9.13.2.11) es equivalente al problema de Sturm-Liouville

(e^3xy′)′ + 2e^3xy + λe^3xy = 0,  y(0) = 0, y(1) = 0.         (9.13.2.12)  ♦

Ejemplo ilustrativo 9.13.2.4

Reescribir el problema de valor propio

x²y′′ + xy′ + λy = 0,  y(1) = 0, y(2) = 0         (9.13.2.13)

del ejemplo 9.13.2.2 como un problema de Sturm-Liouville.

Solución:

Dividiendo la ecuación diferencial en (9.13.2.13) por x² se obtiene

Comparar esto con (9.13.2.7) muestra que u(x) = 1/x, por lo que tomamos U(x) = lnx y p(x) = e^lnx = x.
Multiplicando la ecuación diferencial por x se obtiene

Dado que

xy′′ + y′ = (xy′)′,

(9.13.2.13) es equivalente al problema de Sturm-Liouville

  y(1) = 0,  y(2) = 0.        (9.13.2.14)  ♦

      Los problemas 1 a 4 de la Sección 9.11.1 son problemas de Sturm-Liouville. (El problema 5 no es, aunque algunos autores usan una definición del problema de Sturm-Liouville que lo incluye). Pudimos encontrar los valores propios de los problemas 1 a 4 explícitamente porque en cada problema los coeficientes en las condiciones de contorno satisfacen αβ = 0 y ρδ = 0; es decir, cada condición de contorno involucra ya sea y o y′, pero no ambos. Si esto no es cierto, los valores propios en general no pueden expresarse exactamente mediante fórmulas simples; más bien, los valores aproximados deben obtenerse mediante la solución numérica de ecuaciones derivadas al requerir que los determinantes de ciertos sistemas 2 × 2 de ecuaciones homogéneas sean cero. Para aplicar los métodos numéricos de manera efectiva, se deben usar métodos gráficos para determinar las ubicaciones aproximadas de los ceros de estos determinantes. Luego, los ceros se pueden calcular con precisión mediante métodos numéricos.

Ejemplo ilustrativo 9.13.2.5

Resolver el problema de Sturm-Liouville

y′′ + λy = 0,  y(0) + y′(0) = 0, y(1) + 3y′(1) = 0.        (9.13.2.15)

Solución:

Si λ = 0, la ecuación diferencial en (9.13.2.15) se reduce a y′′ = 0, con solución general y = c₁ + c₂x. Las condiciones de contorno requieren que

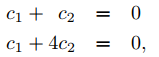
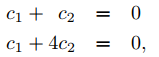
entonces c₁ = c₂ = 0. Por lo tanto, cero no es un valor propio de (9.13.2.15).

        Si λ < 0, escribimos λ = −k² donde k > 0, y la ecuación diferencial en (9.13.2.15) se convierte en y′′ − k²y = 0, con solución general

y = c₁coshkx + c₂senhkx,        (9.13.2.16)

entonces

y′ = k(c₁senhkx + c₂coshkx).

Las condiciones de contorno requieren que

        (9.13.2.17)

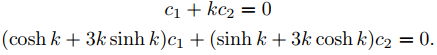
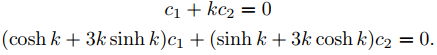
El determinante de este sistema es

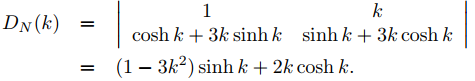
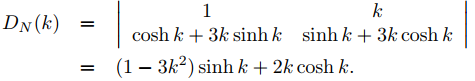
Por lo tanto, el sistema (9.13.2.17) tiene una solución no trivial si y solo si D_N(k) = 0 o, de manera equivalente,

        (9.13.2.18)

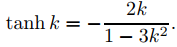
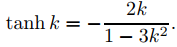
Figura 9.13.2.1  u = tanhk  y  u = −2k/(1 − 3k²)

La gráfica del lado derecho (Figura 9.13.2.1) tiene una asíntota vertical en k = 1/√3. Como los dos lados tienen signos diferentes si k < 1/√3, esta ecuación no tiene solución en (0, 1/√3). La figura 9.13.2.1 muestra las gráficas de los dos lados de (9.13.2.18) en un intervalo a la derecha de la asíntota vertical, que se indica con la línea discontinua. Puede ver que las dos curvas se intersecan cerca de k₀ = 1.2. Dada esta estimación, puede usar el método numérico de Newton para calcular k₀  con mayor precisión. Calculamos k₀ ≈ 1.1219395. Por lo tanto es un valor propio de (9.13.2.15). De (9.13.2.16) y la primera ecuación en (9.13.2.17),

y₀ = k₀coshk₀x − senhk₀x.

      Si λ > 0 escribimos λ = k² donde k > 0, y la ecuación diferencial en (9.13.2.15) se convierte en y′′ + k²y = 0, con solución general

y = cosx + c₂senkx,         (9.13.2.19)

entonces

y′ = k(−c₁senkx + c₂coskx).

Las condiciones de contorno requieren que

        (9.13.2.20)

El determinante de este sistema es

El sistema (9.13.2.20) tiene una solución no trivial si y solo si D_P(k) = 0 o, de manera equivalente,

Figura 9.13.2.2  u = tank  y  u = −2k/(1 + )

La Figura 9.13.2.2 muestra las gráficas de los dos lados de esta ecuación. Puede ver en la figura que las gráficas se intersecan en un número infinito de puntos k_n ≈ nπ (n = 1, 2, 3,. . .), donde el error en esta aproximación tiende a cero cuando n → ∞. Dada esta estimación, puede usar el método de Newton para calcular k_n con mayor precisión. Nosotros calculamos

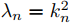
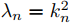
Las estimaciones de los valores propios correspondientes son

De (9.13.2.19) y la primera ecuación en (9.13.2.20),

y_n = k_ncosk_nx − senk_nx

es una función propia asociada con λ_n.  ♦

      Dado que las ecuaciones diferenciales en (9.13.2.12) y (9.13.2.14) son más complicadas que las de (9.13.2.11) y (9.13.2.13) respectivamente, ¿cuál es el sentido del teorema 9.13.2.1? El punto es este: para resolver un problema específico, puede ser mejor tratarlo directamente, como hicimos en los ejemplos 9.13.2.1 y 9.13.2.2; sin embargo, veremos que la transformación del problema general de valores propios (9.13.2.1) al problema de Sturm-Liouville (9.13.2.10) conduce a resultados aplicables a todos los problemas de valores propios de la forma (9.13.2.1).

Teorema 9.13.2.2

Si

Ly = (p(x)y′)′ + q(x)y

y u y v son funciones dos veces diferenciales en [a, b] que satisfacen las condiciones de frontera B₁(y) = 0 y B₂(y) = 0, entonces

        (9.13.2.21)  ♦

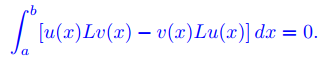
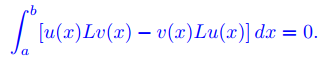
Prueba:

Aplicamos integración por partes para obtener

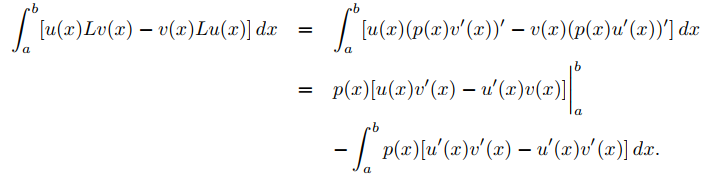
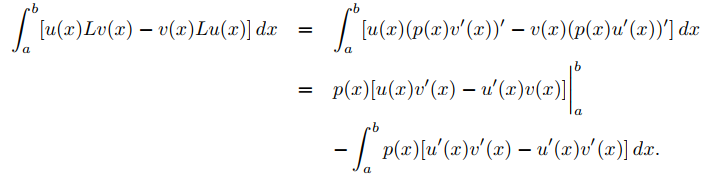
Como la última integral es igual a cero,

      (9.13.2.22) 

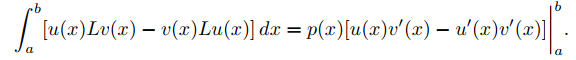
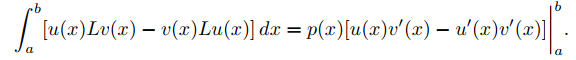
Por suposición, B₁(u) = B₁(v) = 0 y B₂(u) = B₂(v) = 0. Por lo tanto

   y   

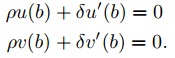
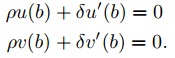
Dado que α² + β² > 0 y ρ² + δ² > 0, los determinantes de estos dos sistemas deben ser cero; esto es,

u(a)v′(a) − u′(a)v(a) = u(b)v′(b) − u′(b)v(b) = 0.

Esto y (9.13.2.22) implican (9.13.2.21), lo que completa la prueba. ♦

        El siguiente teorema muestra que un problema de Sturm-Liouville no tiene valores propios complejos.

Teorema 9.13.2.3

Si λ = p + qi con q ≠ 0 entonces el problema del valor en la frontera

Ly + λr(x)y = 0,   B₁(y) = 0,  B₂(y) = 0

tiene sólo la solución trivial.  ♦

Prueba:

Para que este teorema tenga sentido, debemos considerar soluciones de valores complejos de

Ly + (p + iq)r(x, y)y = 0.         (9.13.2.23)

Si y = u + iv donde u y v tienen valores reales y son dos veces diferenciables, definimos y′ = u′ + iv′ e y′′ = u′′ + iv′′. Decimos que y es una solución de (9.13.2.23) si las partes real e imaginaria del lado izquierdo de (9.13.2.23) son ambas cero. Como Ly = (p(x)′y)′ + q(x)y  y  p, q y r tienen valores reales,

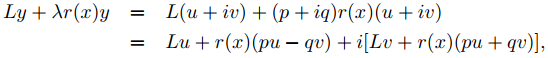
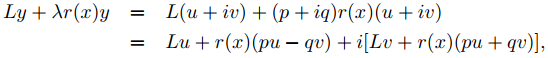
entonces Ly + λr(x)y = 0 si y solo si

Multiplicando la primera ecuación por v y la segunda por u se obtiene

Restando la primera ecuación de la segunda, se obtiene

uLv − vLu + qr(x)(u² + v²) = 0,

entonces

      (9.13.2.24)

Dado que

B₁(y) = B₁(u + iv) = B₁(u) + iB₁(v)

y

B₂(y) = B₂(u + iv) = B₂(u) + iB₂(v),

B₁(y) = 0 y B₂(y) = 0 implican que

B₁(u) = B₂(u) = B₁(v) = B₂(v) = 0.

Por lo tanto, el Teorema 9.13.2.2 implica que la primera integral en (9.13.2.24) es igual a cero, por lo que (9.13.2.24) se reduce a

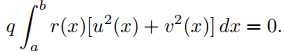
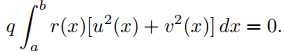
Dado que r es positivo en [a, b] y q ≠ 0 por suposición, esto implica que u ≡ 0 y v ≡ 0 en [a, b].
Por lo tanto y ≡ 0 en [a, b], lo que completa la demostración.  ♦

Teorema 9.13.2.4

Si λ₁ y λ₂ son valores propios distintos del problema de Sturm-Liouville

Ly + λr(x)y = 0,   B₁(y) = 0,  B₂(y) = 0         (9.13.2.25)

con funciones propias asociadas u y v respectivamente, entonces

        (9.13.2.26)  ♦

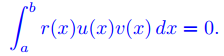
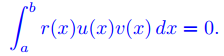
Prueba:

Dado que u y v satisfacen las condiciones de contorno en (9.13.2.25), el Teorema 9.13.2.2 implica que

Dado que Lu = −λ₁ru  y  Lv = −λ₂rv, esto implica que

Como λ₁ ≠ λ₂, esto implica (9.13.2.26), lo que completa la demostración.  ♦

      Si u y v son funciones integrables en [a, b] y

decimos que u y v son ortogonales en [a, b] con respecto a r = r(x).

      El Teorema 9.13.1.1 implica el siguiente teorema.

Teorema 9.13.2.5

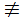
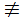
Si u 0 y v ambos satisfacen

Ly + λr(x)y = 0,   B₁(y) = 0,  B₂(y) = 0,

entonces v = cu para alguna constante c.  ♦ 

      Ahora hemos probado partes del siguiente teorema. Una demostración completa está más allá del alcance de este libro.

Teorema 9.13.2.6

El conjunto de todos los valores propios del problema de Sturm-Liouville

Ly + λr(x)y = 0,   B₁(y) = 0,  B₂(y) = 0

se puede ordenar como

λ₁ < λ₂ < · · · < λ_n < · · · ,

y

lim_n→∞ λ_n = ∞.

Para cada n, si y_n es una función propia λ_n arbitraria, entonces cada función propia λ_n es un múltiplo constante de y_n. Si m ≠ n, y_m y y_n son ortogonales [a, b] con respecto a r = r(x); esto es,

      (9.13.2.27)  ♦

      Es posible que desee verificar (9.13.2.27) para las funciones propias obtenidas en los ejemplos 9.13.2.1 y 9.13.2.2. Como conclusión, mencionamos el siguiente teorema. La prueba está más allá del alcance de este libro.

Teorema 9.13.2.7

Sean λ₁ < λ₂ < · · · < λ_n < · · · los valores propios del problema de Sturm-Liouville

Ly + λr(x)y = 0,   B₁(y) = 0,  B₂(y) = 0

con vectores propios asociados y₁, y₂, . . . , y_n, . . .. Supongamos que f es uniforme a trozos (Definición 9.11.2.3) en [a, b]. Para cada n, sea

Entonces

para todo x en el intervalo abierto (a, b).  ♦