| 5. La integral y Técnicas de integración | Ejercicios propuestos para el Capítulo 5.7 |

5.7 Integrales que resultan en funciones trigonométricas inversas

Objetivos de aprendizaje:

5.7.1. Integra funciones que resultan en funciones trigonométricas inversas

    En esta sección nos enfocamos en integrales que resultan en funciones trigonométricas inversas. Hemos trabajado con estas funciones antes. Recuerde de Funciones y sus Gráficas que las funciones trigonométricas no son unívocas a menos que los dominios estén restringidos. Al trabajar con inversas de funciones trigonométricas, siempre debemos tener cuidado de tener en cuenta estas restricciones. También en La Derivada, desarrollamos fórmulas para derivadas de funciones trigonométricas inversas. Las fórmulas desarrolladas allí dan lugar directamente a fórmulas de integración que implican funciones trigonométricas inversas.

Integrales que dan como resultado funciones de seno inverso

Comencemos esta última sección del capítulo enseñando las siguientes tres fórmulas. Junto con estas fórmulas, usamos la sustitución u para evaluar las integrales. Probamos la fórmula para la integral seno inversa.

REGLA 5.7.1 : FÓRMULAS DE INTEGRACIÓN RESULTANTES EN FUNCIONES TRIGONOMÉTRICAS INVERSAS

Las siguientes fórmulas de integración producen funciones trigonométricas inversas:

\(\begin{aligned} \int \frac{du}{\sqrt{a^2 – u^2}} &= \operatorname{sen}^{-1} \frac{u}{a} + C \\ \int \frac{du}{a^2 + u^2} &= \frac{1}{a} \operatorname{tan}^{-1} \frac{u}{a} + C \\ \int \frac{du}{u\sqrt{u^2 – a^2}} &= \frac{1}{a} \operatorname{sec}^{-1} \frac{u}{a} + C \end{aligned}\)

♦

Prueba

Sea y = sen‾¹(x/a). Entonces aseny = x. Ahora usemos la diferenciación implícita. ObtenemosPara −π/2≤ y ≤ π/2, cosy ≥ 0. Así, aplicando la identidad pitagórica sen²y + cos²y = 1, tenemos que cosy = √(1 – sen²y). Esto da

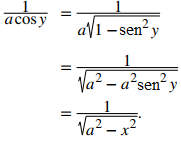Entonces para −a ≤ x ≤ a, y generalizando a u, tenemos que♦

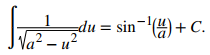EJEMPLO ILUSTRATIVO 5.6_1. Evaluación de una integral definida usando funciones trigonométricas inversas

Evaluar la integral definida

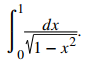
Solución:
Podemos ir directamente a la fórmula para la antiderivada en la regla sobre fórmulas de integración que resultan en funciones trigonométricas inversas, y luego evaluar la integral definida. Tenemos

♦

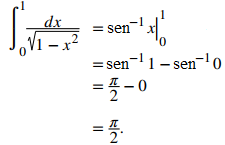Ejercicio de control 5.7.1

Evalúa la integral \(\int \frac{dx}{\sqrt{1 – 16x^2}}\). ♦

EJEMPLO ILUSTRATIVO 5.6_2. Encontrar una antiderivada que implique una función trigonométrica inversa

Evaluar la integral

Solución:
Sustituye u = 3x. Entonces du = 3dx y tenemos

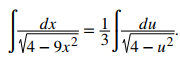
Aplicando la fórmula con a = 2, obtenemos

♦

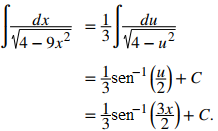Ejercicio de control 5.7.2

Encuentra la integral indefinida usando una función trigonométrica inversa y la sustitución para \(\int \frac{dx}{\sqrt{9 – x^2}}\). ♦

EJEMPLO ILUSTRATIVO 5.6_3. Evaluación de una integral definida

Evaluar la integral definida

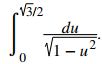
Solución:
El formato del problema coincide con la fórmula del seno inverso. Así,

♦

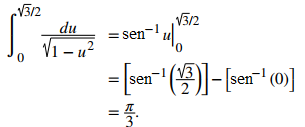Integrales que resultan en otras funciones trigonométricas inversas

Hay seis funciones trigonométricas inversas. Sin embargo, solo se observan tres fórmulas de integración en la regla sobre fórmulas de integración que dan como resultado funciones trigonométricas inversas porque las tres restantes son versiones negativas de las que usamos. La única diferencia es si el integrando es positivo o negativo. En lugar de memorizar tres fórmulas más, si el integrando es negativo, simplemente se factoriza por -1 y se evalúa la integral usando una de las fórmulas ya proporcionadas. Para cerrar esta sección, examinamos una fórmula más: la integral que resulta en la función de tangente inversa.

EJEMPLO ILUSTRATIVO 5.6_4. Encontrar una antiderivada que implique la función tangente inversa

Encuentre una antiderivada de

Solución:
Comparando este problema con las fórmulas establecidas en la regla sobre fórmulas de integración que resultan en funciones trigonométricas inversas, el integrando se parece a la fórmula para tan⁻¹u + C. Entonces usamos sustitución u, tomando u = 2x, luego du = 2dx y 1/2du = dx. Entonces tenemos que

♦

Ejercicio de control 5.7.3

Usa la sustitución para encontrar la antiderivada \(\int \frac{dx}{25 + 4x^2}\). ♦

EJEMPLO ILUSTRATIVO 5.6_5. Aplicando las fórmulas de integración

Encuentra la antiderivada de

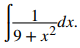
Solución:
Aplica la fórmula con a = 3. Entonces,

♦

Ejercicio de control 5.7.4

Evalúa la integral \(\int \frac{dx}{16 + x^2}\). ♦

EJEMPLO ILUSTRATIVO 5.6_6. Evaluación de una integral definida

Evaluar la integral definida

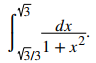
Solución:
Usa la fórmula para la tangente inversa. Tenemos

♦

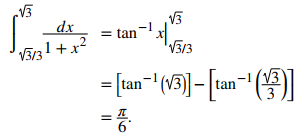Ejercicio de control 5.7.5

Evalúa la integral definida \(\int_{0}^{2} \frac{dx}{4 + x^2}\). ♦