| 1. Funciones y sus gráficas | 1.5 Funciones exponenciales y logarítmicas |
Ejercicios propuestos del capítulo 1.5
Para los siguientes ejercicios, evalúe las funciones exponenciales dadas como se indica, con una precisión de dos dígitos significativos después del decimal.
229. f (x) = 5ˣ a. x = 3 b. x = 12 c. x = √2
230. f (x) = (0.3)ˣ a. x = −1 b. x = 4 c. x = −1.5
231. f (x) = 10ˣ a. x = −2 b. x = 4 c. x = 53
232. f (x) = eˣ a. x = 2 b. x = −3,2 c. x = π
Para los siguientes ejercicios, combine la ecuación exponencial con la gráfica correcta.
a. y = 4⁻ˣ
b. y = 3ˣ ⁻¹
c. y = 2ˣ ⁺¹
d. y = (12)ˣ + 2
e. y = −3⁻ˣ
f. y = 1−5ˣ
233.
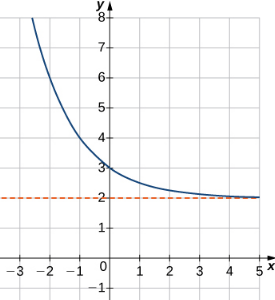
234.
235.
236.
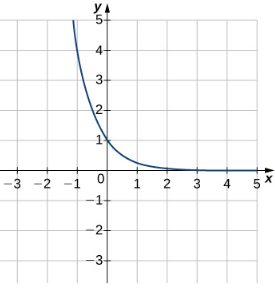
237.
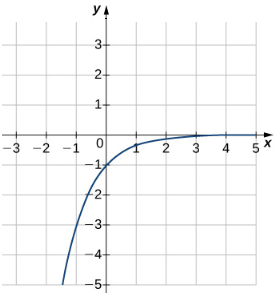
238.
Para los siguientes ejercicios, dibuje la gráfica de la función exponencial. Determine el dominio, el rango y la asíntota horizontal.
239. f (x) = eˣ + 2 (Ver solución)
240. f (x) = – 2ˣ
241. f (x) = 3ˣ ⁺¹
242. f (x) = 4ˣ − 1 (Ver solución)
Para los siguientes ejercicios, escriba la ecuación en forma exponencial equivalente.
246. log₃81 = 4
247. log₈2 = 1/3
248. log₅1 = 0
249. log₅25 = 2
250. log 0.1 = −1
251. ln (1/e³) = – 3
252. log₉3 = 0.5
253. ln1 = 0
Para los siguientes ejercicios, escriba la ecuación en forma logarítmica equivalente.
254. 2³ = 8
255. 4⁻² = 1/16
256. 10² = 100
257. 9º = 1
258. (1/3)³ = 1/27
260. eˣ = y
261. 9ʸ = 150
262. b³ = 45
Para los siguientes ejercicios, dibuje la gráfica de la función logarítmica. Determine el dominio, el rango y la asíntota vertical.
264. f (x) = 3 + lnx
265. f (x) = ln (x − 1)
266. f (x) = ln (−x)
267. f (x) = 1 − lnx
268. f (x) = logx − 1
269. f (x) = ln (x + 1)
Para los siguientes ejercicios, use las propiedades de los logaritmos para escribir las expresiones como una suma, diferencia y / o producto de logaritmos.
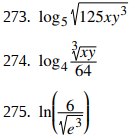
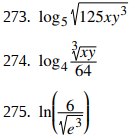
Para los siguientes ejercicios, resuelva la ecuación exponencial exactamente.
Para los siguientes ejercicios, resuelva la ecuación logarítmica exactamente, si es posible.
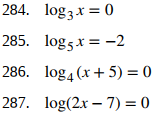
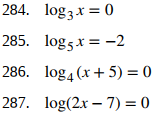
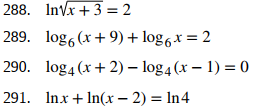
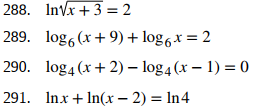
Para los siguientes ejercicios, use la fórmula de cambio de base y base 10 o base e para evaluar las expresiones dadas. Responda en forma exacta y en forma aproximada, redondeando a cuatro decimales.
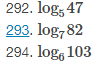
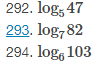
298. Reescribe las siguientes expresiones en términos de exponenciales y simplifica.
a. 2cosh (lnx) b. cosh4x + senh4x c. cosh2x − senh2x d. ln (coshx + senhx) + ln (coshx − senhx)
299. [T] El número de bacterias N en un cultivo después de t días puede ser modelado por la función
Encuentre la cantidad de bacterias presentes después de 15 días.
300. [T] La demanda D (en millones de barriles) de petróleo en un país rico en petróleo viene dada por la función
donde p es el precio (en dólares) de un barril de petróleo Encuentre la cantidad de petróleo demandada (al millón de barriles más cercano) cuando el precio oscila entre $ 15 y $ 20.
301. [T] El monto A de una inversión de $ 100,000 pagando continuamente y compuesto por t años viene dado por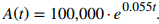
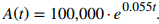
Encuentre la cantidad A acumulada en 5 años.
302. [T] Una inversión se compone mensualmente, trimestralmente o anualmente y viene dada por la función
donde A es el valor de la inversión en el tiempo t, P es el capital inicial que fue invertido, j es la tasa de interés anual y n es el número de veces que el interés se capitaliza por año. Dada una tasa de interés anual de 3.5% y un capital inicial de $ 100,000, calcule la cantidad A acumulada en 5 años para intereses compuestos a. diariamente, b. mensualmente, c. trimestralmente, y d. anual.
303. [T] La concentración de iones de hidrógeno en una sustancia se denota por [H⁺], medida en moles por litro. El pH de una sustancia se define por la función logarítmica pH = −log [H⁺]. Esta función se usa para medir la acidez de una sustancia. El pH del agua es 7. Una sustancia con un pH inferior a 7 es un ácido, mientras que una que tiene un pH superior a 7 es una base.
- Encuentre el pH de las siguientes sustancias. Redondea las respuestas a un dígito.
- Determine si la sustancia es un ácido o una base.
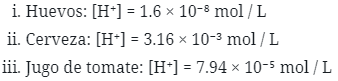
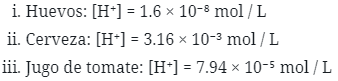
304. [T] El yodo-131 es una sustancia radiactiva que se desintegra de acuerdo con la función
donde Q0 es la cantidad inicial de una muestra de la sustancia y t es en días. Determine cuánto tiempo tarda (hasta el día más cercano) en descomponerse el 95% de una cantidad.
305. [T] Según el Banco Mundial, a fines de 2013 (t = 0) la población de EE. UU. Era de 316 millones y aumentaba según el siguiente modelo:
donde P se mide en millones de personas yt se mide en años posteriores a 2013.
- Según este modelo, ¿cuál será la población de los Estados Unidos en 2020?
- Determine cuándo la población de EE. UU. Será el doble de lo que es en 2013.
306. [T] El monto A acumulado después de 1000 dólares se invierte durante t años a una tasa de interés del 4% está modelado por la función A (t) = 1000 (1.04)ᵗ.
- Encuentre la cantidad acumulada después de 5 años y 10 años.
- Determine cuánto tiempo tarda la inversión original en triplicarse.
307. [T] Se sabe que una colonia bacteriana cultivada en un laboratorio se duplica en 12 horas. Supongamos, inicialmente, que hay 1000 bacterias presentes.
- Use la función exponencial Q = Q0eᵏᵗ para determinar el valor k, que es la tasa de crecimiento de la bacteria. Redondea a cuatro decimales.
- Determine aproximadamente cuánto tardan en crecer 200,000 bacterias.
308. [T] La población de conejos en una reserva de caza se duplica cada 6 meses. Supongamos que hay 120 conejos inicialmente.
- Use la función exponencial P = P0aᵗ para determinar la constante de tasa de crecimiento a. Redondea a cuatro decimales.
- Use la función en la parte a. para determinar aproximadamente cuánto tiempo tarda la población de conejos en llegar a 3500.
309. [T] El terremoto de 1906 en San Francisco tuvo una magnitud de 8.3 en la escala de Richter. Al mismo tiempo, en Japón, un terremoto de magnitud 4.9 causó daños menores. Aproximadamente, ¿cuánta más energía fue liberada por el terremoto de San Francisco que por el terremoto japonés?