| 1. Funciones y sus gráficas | 1.5 Funciones exponenciales y logarítmicas |

Funciones logarítmicas

       Usando nuestra comprensión de las funciones exponenciales, podemos discutir sus inversas, que son las funciones logarítmicas. Estas son útiles cuando necesitamos considerar cualquier fenómeno que varíe en un amplio rango de valores, como por ejemplo el pH en química o decibelios en los niveles de sonido.

La función exponencial f (x) = bˣ es uno a uno, con dominio (−∞, ∞) y rango (0, ∞). Por lo tanto, tiene una función inversa, llamada función logarítmica con base b. Para cualquier b > 0, b ≠ 1, la función logarítmica con base b, denotada log_b, tiene dominio (0, ∞) y rango (−∞, ∞), y satisface

log_b(x) = y  si y sólo si  bʸ = x.

Por ejemplo,

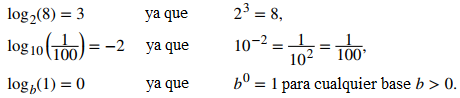
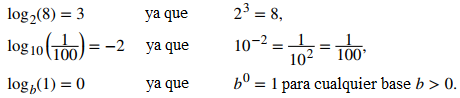
Además, dado que y = log_b(x)  e  y = bˣ son funciones inversas,

La función logarítmica más utilizada es la función log_e. Como esta función utiliza e (base de la función exponencial natural) como base, se llama función logaritmo natural. Aquí usamos la notación ln(x) o lnx para significar log_e(x). Por ejemplo,

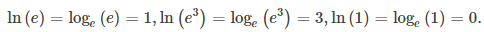
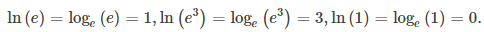
Como las funciones f (x) = eˣ y g(x) = ln(x) son inversas entre sí,

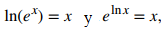
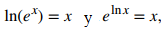
y sus gráficas son simétricas con respecto a la recta y = x (Figura 1.5_4).

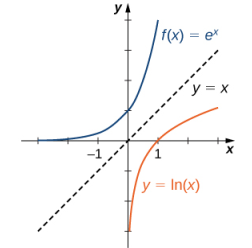
(Figura 1.5_4 Las funciones y = eˣ e y = ln(x) son inversas entre sí, por lo que sus gráficas son simétricas con respecto a la recta y = x.)

    En general, para cualquier base b > 0, b ≠ 1, la función g(x) = log_b(x) es simétrica respecto de la recta y = x con la función f (x) = bˣ. Usando este hecho y las gráficas de las funciones exponenciales, graficamos las funciones log_b para varios valores de b > 1 (Figura 1.5_5).

(Figura 1.5_5 Los gráficas de y = log_b(x) se representan para b = 2, e, 10.)

REGLA 1.5.2: PROPIEDADES DE LOS LOGARITMOS

Si a, b, c > 0, b ≠ 1 y r es cualquier número real, entonces

Ejemplo ilustrativo 1.5_4  Resolver ecuaciones que involucran funciones exponenciales

Resuelve cada una de las siguientes ecuaciones para x.
a.  5ˣ = 2
b.  eˣ + 6e⁻ˣ = 5

Solución:
a. Aplicando la función logaritmo natural a ambos lados de la ecuación, tenemos

ln5ˣ = ln2. 

Usando la propiedad de la potencia de los logaritmos,

xln5 = ln2. 

Por lo tanto,

x = ln2 / ln5.

 

b.  Multiplicando ambos lados de la ecuación por eˣ, llegamos a la ecuación

e²ˣ + 6 = 5eˣ. 

Reescribiendo esta ecuación como

e²ˣ  – 5eˣ + 6 = 0, 

entonces podemos reescribirla como una ecuación cuadrática en eˣ:

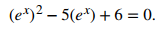
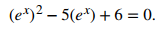
Ahora podemos resolver la ecuación cuadrática. Factorizando esta ecuación, obtenemos

(eˣ − 3) (eˣ − 2) = 0. 

Por lo tanto, las soluciones satisfacen eˣ = 3 y eˣx = 2. Tomar el logaritmo natural de ambos lados nos da las soluciones x = ln3, ln2. ◊

EJERCICIO DE CONTROL 1.5_4

Resolver e²ˣ / (3 + e²ˣ) = 1/2.

Ejemplo ilustrativo 1.5_5 Resolver ecuaciones que involucran funciones logarítmicas

Resuelve cada una de las siguientes ecuaciones para x.
a.  ln (1/x) = 4

b.  log₁₀√x + log₁₀x = 2

c.  ln (2x) − 3ln (x²) = 0

Solución:
a.  Por la definición de la función logaritmo natural,

ln (1/x) = 4  si y sólo si  e⁴ = 1/x. 

Por lo tanto, la solución es x = 1 / e⁴.

b.  Usando las propiedades del producto y potencia de las funciones logarítmicas, reescribe el lado izquierdo de la ecuación como

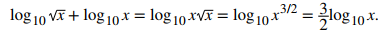
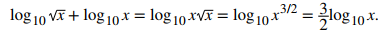
Por lo tanto, la ecuación puede reescribirse como

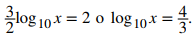
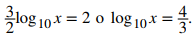
La solución es

c.  Usando la propiedad de la potencia de los logaritmos, podemos reescribir la ecuación como

ln(2x) − ln(x⁶) = 0.

Ahora, usando la propiedad del cociente, esto se convierte en

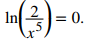
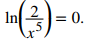
Por lo tanto, 2/x⁵ = 1, lo que implica

(Es conveniente verificar que no haya una solución extraña.) ◊

EJERCICIO DE CONTROL 1.5_5

Resolver ln(x³) −4ln(x) = 1.

    Al evaluar una función logarítmica con una calculadora, puede haber notado que las únicas opciones son log10 o log, llamado logaritmo común, o ln, que es el logaritmo natural. Sin embargo, las funciones exponenciales y las funciones de logaritmo se pueden expresar en términos de cualquier base b deseada. Si necesita usar una calculadora para evaluar una expresión con una base diferente, puede aplicar primero las fórmulas de cambio de base. Usando este cambio de base, típicamente escribimos una función exponencial o logarítmica dada en términos de las funciones exponenciales y logarítmicas naturales.

REGLA 1.5.3: FORMULAS DE CAMBIO DE BASE

Sea a > 0, b > 0 y a ≠ 1, b ≠ 1.

Ejemplo ilustrativo 1.5_6  Cambio de base

Use una calculadora para evaluar log₃7 con la fórmula de cambio de base presentada anteriormente.

EJERCICIO DE CONTROL 1.5_6

Use la fórmula de cambio de base y una calculadora para evaluar log₄6.

Ejemplo ilustrativo 1.5_7   La escala de Richter para terremotos

En 1935, Charles Richter desarrolló una escala (ahora conocida como la escala de Richter) para medir la magnitud de un terremoto. La escala es una escala logarítmica de base 10, y se puede describir de la siguiente manera: considere un terremoto con magnitud R₁ en la escala de Richter y un segundo terremoto con magnitud R₂ en la escala de Richter. Supongamos que R₁ > R₂, lo que significa que el terremoto de magnitud R₁ es más fuerte, pero ¿cuánto más fuerte es que el otro terremoto? Una forma de medir la intensidad de un terremoto es usando un sismógrafo para medir la amplitud de las ondas del terremoto. Si A₁ es la amplitud medida para el primer terremoto y A₂ es la amplitud medida para el segundo terremoto, entonces las amplitudes y magnitudes de los dos terremotos satisfacen la siguiente ecuación:

Considere un terremoto que mide 8 en la escala de Richter y un terremoto que mide 7 en la escala de Richter. Entonces,

Por lo tanto,

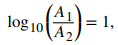
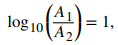
lo que implica A₁ / A₂ = 10 o A₁ = 10A₂. Dado que A₁ es 10 veces el tamaño de A₂, decimos que el primer terremoto es 10 veces más intenso que el segundo terremoto. Por otro lado, si un terremoto mide 8 en la escala de Richter y otro mide 6, entonces la intensidad relativa de los dos terremotos satisface la ecuación

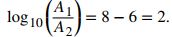
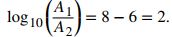
Por lo tanto, A₁ = 100A₂. Es decir, el primer terremoto es 100 veces más intenso que el segundo terremoto.

¿Cómo podemos usar las funciones logarítmicas para comparar la gravedad relativa del terremoto de magnitud 9 en Japón en 2011 con el terremoto de magnitud 7.3 en Haití en 2010?

Solución:
Para comparar los terremotos de Japón y Haití, podemos usar la ecuación presentada anteriormente:

Por lo tanto,

y concluimos que el terremoto en Japón fue aproximadamente 50 veces más intenso que el terremoto en Haití.  ◊

EJERCICIO DE CONTROL 1.5_7

Compare la gravedad relativa de un terremoto de magnitud 8.4 con un terremoto de magnitud 7.4.