| 1. Funciones y sus gráficas | 1.5 Funciones exponenciales y logarítmicas |
Ejercicios resueltos del Capítulo 1.5
239. f (x) = eˣ + 2. Dibuje la gráfica de la función exponencial. Determine el dominio, el rango y la asíntota horizontal.
Solución – Juan Beltrán:
El dominio de f son todos los reales (e se puede elevar a cualquier número real). Se tiene entonces que
f (x) = eˣ + 2, domf = (−∞, ∞).
Además,
- Cuando x → +∞, eˣ → +∞ y, por consiguente eˣ + 2 → +∞.
- Cuando x → −∞, eˣ → 0 y, por ende eˣ + 2 → 2; de tal modo que y = 2 es una asíntota horizontal. Y el rango de f es (2, ∞).
- f (0) = e º + 2 =1 + 2 = 3: Corte con el ejey.
- eˣ + 2 es la suma de dos números positivos (nunca da 0): No hay cortes con el ejex.
- Para toda x₂ > x₁, f (x₂) > f (x₁): f es monótona creciente.
Teniendo presente los datos anteriores trazamos la gráfica de f :
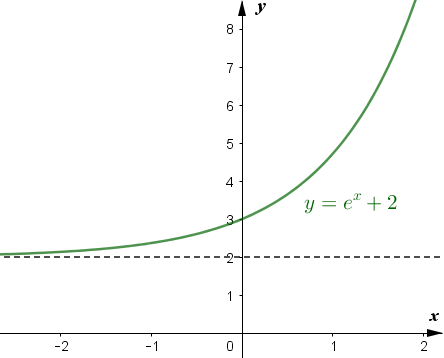

Para los siguientes ejercicios, dibuje la gráfica de la función exponencial. Determine el dominio, el rango y la asíntota horizontal.
242. f (x) = 4ˣ − 1
243. f (x) = 1−2⁻ˣ
