| 1. Funciones y sus gráficas | 1.5 Funciones exponenciales y logarítmicas |
El número e
Un tipo especial de función exponencial aparece con frecuencia en aplicaciones del mundo real. Para describirlo, considere el siguiente ejemplo de crecimiento exponencial, que surge del interés compuesto en una cuenta de ahorro. Suponga que una persona invierte P dólares en una cuenta de ahorros con una tasa de interés anual r, compuesta anualmente. La cantidad de dinero después de 1 año es
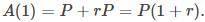
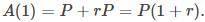
La cantidad de dinero después de 2 años es
Más generalmente, la cantidad después de t años es
La cantidad de dinero después de 1 año es
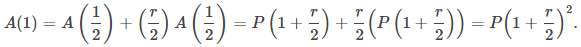
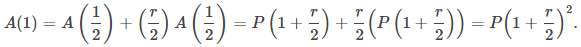
Después de t años, la cantidad de dinero en la cuenta es
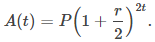
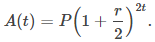
¿Qué sucede cuando n → ∞? Para responder a esta pregunta, dejamos m = n/r y escribimos
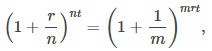
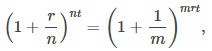
y examine el comportamiento de (1 + 1/m) ͫ cuando m → ∞, usando una tabla de valores (Tabla 1.12).
Mirando esta tabla, parece que (1 + 1/m) ͫ se aproxima a un número entre 2.7 y 2.8 cuando m → ∞. De hecho, (1 + 1/m) ͫ se aproxima a un número particular cuando m → ∞. Llamamos a este número e. Con seis decimales de precisión,
e ≈ 2.718282.
La letra e fue utilizada por primera vez para representar este número por el matemático suizo Leonhard Euler durante la década de 1720. Aunque Euler no descubrió el número, mostró muchas conexiones importantes entre e y las funciones logarítmicas. Todavía usamos la notación e hoy para honrar el trabajo de Euler porque aparece en muchas áreas de las matemáticas y porque podemos usarlo en muchas aplicaciones prácticas.
Volviendo a nuestro ejemplo de cuenta de ahorro, podemos concluir que si una persona pone P dólares en una cuenta a una tasa de interés anual r, compuesta continuamente, entonces A(t) = Peʳᵗ. Esta función puede ser familiar. Dado que las funciones que involucran la base e surgen a menudo en las aplicaciones, damos a la función f (x) = eˣ un nombre especial, la función exponencial natural. Esta función no solo es interesante debido a la definición del número e, sino que, como se discute a continuación, su gráfica tiene una propiedad importante.
Como e > 1, sabemos que eˣ está creciendo en (−∞, ∞). En la figura 1.5_3, mostramos una gráfica de f (x) = eˣ junto con una recta tangente a la gráfica de f en x = 0. Damos una definición precisa de recta tangente en el próximo capítulo; pero, informalmente, decimos que una recta tangente a una gráfica de f en x = a es una recta que pasa por el punto (a, f (a)) y tiene la misma “pendiente” que f en ese punto. La función f (x) = eˣ es la única función exponencial bˣ con recta tangente en x = 0 que tiene una pendiente de 1. Como vemos más adelante en el texto, tener esta propiedad hace que la función exponencial natural sea la función exponencial más simple para uso en muchos casos.
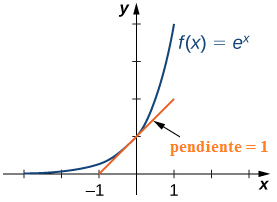
(Figura 1.5_3 La gráfica de f (x) = eˣ tiene una recta tangente con pendiente 1 en x = 0.)
Ejemplo ilustrativo 1.5_3 Interés Compuesto
Suponga que $500 se invierten en una cuenta a una tasa de interés anual r = 5.5%, compuesto continuamente.
- Deje t denotar el número de años después de la inversión inicial y A(t) denote la cantidad de dinero en la cuenta en el momento t. Encuentre una fórmula para A(t).
- Encuentre la cantidad de dinero en la cuenta después de 10 años y después de 20 años.
Solución:
a. Si se invierten P dólares en una cuenta a una tasa de interés anual r, compuesta continuamente, entonces A(t) = Peʳᵗ. Aquí P = $500 y r = 0.055. Por lo tanto,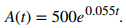
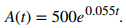
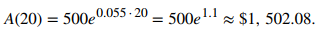
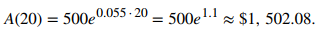
b. Después de 10 años, la cantidad de dinero en la cuenta es
Después de 20 años, la cantidad de dinero en la cuenta es
EJERCICIO DE CONTROL 1.5_3
Si se invierten $750 en una cuenta a una tasa de interés anual del 4%, compuesta continuamente, encuentre una fórmula para la cantidad de dinero en la cuenta después de t años. Encuentre la cantidad de dinero después de 30 años.