| 1. Funciones y sus gráficas | 1.2. Clases básicas de funciones |

Ejercicios propuestos para Capítulo 1.2

    Para los siguientes ejercicios, para cada par de puntos,  a. encuentre la pendiente de la recta que pasa por los puntos y  b. indica si la recta está creciendo, decreciendo, es horizontal o vertical.

    Para los siguientes ejercicios, escriba la ecuación de la recta que satisfaga las condiciones dadas en forma de pendiente-intersección.

    Para los siguientes ejercicios, para cada ecuación lineal,  a. dé la pendiente m y y-intercepción, si la hay, y  b. grafica la recta.

    Para los siguientes ejercicios, para cada polinomio,  a. encuentra el grado; b. encuentra los ceros, si los hay;  c. encuentre la(s) intersección(es), si hay alguna;  d. use el coeficiente principal para determinar el comportamiento final de la gráfica; y  e. determinar algebraicamente si el polinomio es par, impar o ninguno.

    Para los siguientes ejercicios, use la gráfica de f (x) = x² para representar gráficamente cada función transformada g.

    Para los siguientes ejercicios, use la gráfica de f (x) = √x para representar gráficamente cada función transformada g.

    Para los siguientes ejercicios, use la gráfica de y = f (x) para representar gráficamente cada función transformada g.

    En los siguientes ejercicios, para cada una de las funciones definidas por partes,  a. evalúe el valor de la función para los valores dados de la variable independiente y  b. Dibuja la gráfica de la función.

    Para los siguientes ejercicios (98 a 102), determine si la afirmación es verdadera o falsa. Explicar por qué.

98. f (x) = (4x + 1) / (7x − 2) es una función trascendental.

99. La siguiente es una función racional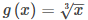

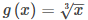
100. Una función logarítmica es una función algebraica.

101. Una función de la forma f (x) = xᵇ, donde b es una constante de valor real, es una función exponencial.

102. El dominio de una función raíz par son todos los números reales.

103. [T] Una empresa compra algunos equipos informáticos por un valor de $20,500.

Al final de un período de 3 años, el valor del equipo ha disminuido linealmente a $12,300.

1. Encuentre una función y = V(t) que determine el valor V del equipo al final de t años.
2. Encuentre e interprete el significado de los interceptos con los ejes para esta situación.
3. ¿Cuál es el valor del equipo al final de 5 años?
4. ¿Cuándo será el valor del equipo $3000?              Ver la solución del Ejercicio 1.2_103

104. [T] El total de compras en línea durante las vacaciones de Navidad ha aumentado dramáticamente durante los últimos 5 años.             

En 2012 (t = 0), las ventas totales de vacaciones en línea fueron de $42.3 mil millones,

mientras que en 2013 fueron de $48.1 mil millones.

1. Encuentre una función lineal S que calcule las ventas totales de vacaciones en línea en el año t.
2. Interpreta la pendiente de la gráfica de S.
3. Use la parte a. para predecir el año en que las compras en línea durante la Navidad alcanzarán los $60 mil millones.              Ver la solución del Ejercicio 1.2_104

105. [T] Una panadería familiar hace pastelitos y los vende en festivales locales al aire libre. Para un festival de música, hay un costo fijo de $125 para instalar un puesto de magdalenas.

El propietario estima que cuesta $0.75 hacer cada cupcake. El propietario está interesado en determinar el costo total C en función del número de pastelitos hechos.

1. Encuentre una función lineal que relacione el costo C con x, el número de pastelitos hechos.
2. Encuentra el costo para hornear 160 cupcakes.
3. Si el propietario vende los pastelitos por $1.50 cada uno, ¿cuántos pastelitos necesita vender para comenzar a obtener ganancias? (Sugerencia: use la función INTERSECCIÓN en una calculadora para encontrar este número).

106. [T] Se espera que una casa comprada por $250,000 valga el doble de su precio de compra en 18 años.

1. Encuentre una función lineal que modele el precio P de la casa versus el número de años t desde la compra original.
2. Interpreta la pendiente de la gráfica de P.
3. Encuentre el precio de la casa 15 años después de la compra original.

107. [T] Se compró un automóvil por $26,000.

El valor del automóvil se deprecia en $1500 por año.

1. Encuentre una función lineal que modele el valor V del automóvil después de t años.
2. Encuentra e interpreta V(4).

108. [T] Se compró un condominio en una parte exclusiva de la ciudad por $432,000.

En 35 años vale $60,500. Encuentra la tasa de depreciación.

109. [T] El costo total C (en miles de dólares) para producir un determinado artículo está modelado por la función lineal C(x) = 10.50x + 28,500, donde x es el número de artículos producidos. Determine el costo para producir 175 artículos.

Ver la solución del Ejercicio 1.2_109

110. [T] Un profesor le pide a su clase que informe la cantidad de tiempo que pasaron escribiendo dos tareas. La mayoría de los estudiantes informan que les toma aproximadamente 45 minutos escribir una tarea de cuatro páginas y aproximadamente 1.5 horas para escribir una tarea de nueve páginas.

1. Encuentre una función lineal y = N(t) que modela esta situación, donde N es el número de páginas escritas y t es el tiempo en minutos.
2. Use la parte a. para determinar cuántas páginas se pueden escribir en 2 horas.
3. Use la parte a. para determinar cuánto tiempo lleva escribir una asignación de 20 páginas.

111. [T] La producción (como porcentaje de la capacidad total) de las centrales nucleares en los Estados Unidos puede modelarse mediante la función lineal  P(t) = 1.8576t + 68.052, donde t es el tiempo en años y t = 0 corresponde a principios de 2000. Use el modelo para predecir el porcentaje de producción en 2015.

112. [T] La oficina de admisiones de una universidad pública estima que el 65% de los estudiantes a los que ofrecieron admisión a la clase de 2019 se inscribirán realmente.

1. Encuentre la función lineal y = N(x), donde N es el número de estudiantes que realmente se inscriben y x es el número de todos los estudiantes a los que se les ofreció admisión a la clase de 2019.
2. Si la universidad quiere que el tamaño de la clase de primer año de 2019 sea 1350, determine cuántos estudiantes deben ser admitidos.