| 1. Funciones y sus gráficas | 1.2. Clases básicas de funciones |

Funciones algebraicas

Al permitir cocientes y potencias con exponentes racionales en funciones polinomiales, creamos una clase más grande de funciones. Una función algebraica es aquella que implica suma, resta, multiplicación, división, potencias racionales y raíces. Dos tipos de funciones algebraicas son funciones racionales y funciones raíz.

Así como los números racionales son cocientes de enteros, las funciones racionales son cocientes de polinomios. En particular, una función racional es cualquier función de la forma f (x) = p(x)/q(x), donde p(x)  y  q(x) son polinomios. Por ejemplo,

Son funciones racionales.

EJEMPLO ILUSTRATIVO 1.2_5. Encontrar dominio y rango para funciones algebraicas

Para cada una de las siguientes funciones, deduzca el dominio y el rango.
a.   f (x) = (3x − 1)/(5x + 2)
b.  f (x) = √(4 – x²). 

Solución:
a.   No es posible dividir por cero, por lo que el dominio es el conjunto de números reales x tal que x ≠ −2/5.

Para encontrar el rango, necesitamos encontrar los valores de y para los cuales existe un número real x tal que

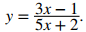
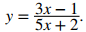
Cuando multiplicamos ambos lados de esta ecuación por 5x + 2, vemos que x debe satisfacer la ecuación

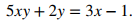
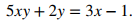
De esta ecuación, podemos ver que x debe satisfacer

Si y = 3/5, esta ecuación no tiene solución. Por otro lado, mientras y ≠ 3/5,

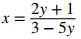
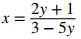
satisface esta ecuación. Podemos concluir que el rango de f es {y|y ≠ 3/5}.

b.   Para encontrar el dominio de f, necesitamos 4 − x² ≥ 0. Cuando factorizamos la diferencia de cuadrados, escribimos 4 − x² = (2 − x)(2 + x) ≥ 0. Esta desigualdad se cumple si y sólo si ambos términos son positivos o ambos términos son negativos. Para que ambos términos sean positivos, necesitamos encontrar x tal que

2 − x ≥ 0   y   2 + x ≥ 0.

Estas dos desigualdades se reducen a 2 ≥ x y x ≥ − 2. Por lo tanto, el conjunto {x| −2 ≤ x ≤ 2} debe ser parte del dominio. Para que ambos términos sean negativos, necesitamos que

2 − x ≤ 0  y  2 + x ≥ 0.

Estas dos desigualdades también se reducen a 2 ≤ x y x ≥ − 2. No hay valores de x que satisfagan ambas desigualdades. Por lo tanto, podemos concluir que el dominio de esta función es {{x| −2 ≤ x ≤ 2}.
Si −2 ≤ x ≤ 2, entonces 0 ≤ 4 − x² ≤ 4. Por lo tanto, 0 ≤ √(4 − x²) ≤ 2, y el rango de f es {y| 0 ≤ y ≤ 2}. ◊

EJERCICIO DE CONTROL 1.2_3 

Encuentre el dominio y el rango para la función f (x) = (5x + 2)/(2x − 1).

Funciones raíz o radicales

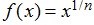
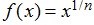
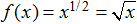
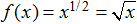
Una función raíz es una función potencia de la formadonde n es un entero positivo mayor que uno. Por ejemplo,es la función de raíz cuadrada y

es la función de raíz cúbica.

     Al permitir composiciones de funciones raíz y funciones racionales, podemos crear otras funciones algebraicas. Por ejemplo,es una función algebraica.

Las funciones raíz f (x) = x¹ﺍ ⁿ   tienen características definitorias dependiendo de si n es par o impar. Para todos los enteros pares n ≥ 2, el dominio de f (x) = x¹ﺍ ⁿ  es el intervalo [0, ∞). Para todos los enteros impares n ≥ 1, el dominio de f (x) = x¹ﺍ ⁿ  es el conjunto de todos los números reales. Como x¹ﺍ ⁿ = (- x) ^{1 / n}  para enteros impares n,  f (x) = x¹ﺍ ⁿ  es una función impar si n es impar. Vea las gráficas de las funciones raíz para diferentes valores de n en la Figura 1.2_7.

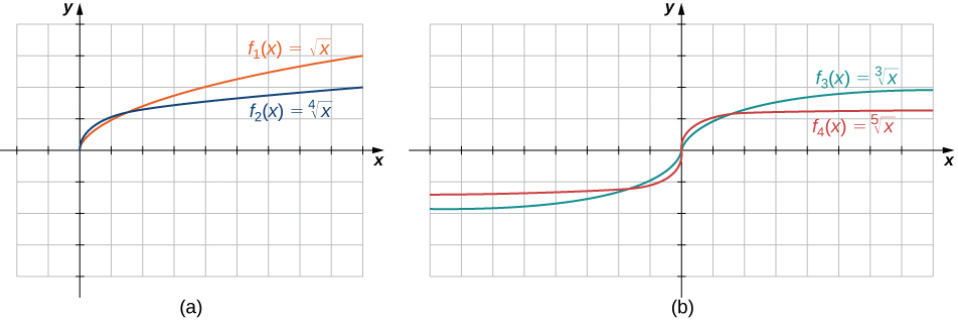
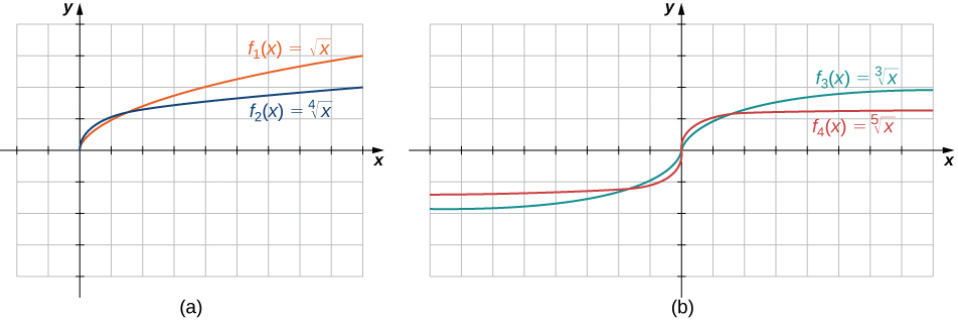
EJEMPLO ILUSTRATIVO 1.2_6. Encontrar dominios para funciones algebraicas

Para cada una de las siguientes funciones, determine el dominio de la función.

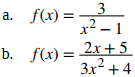
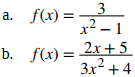
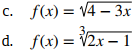
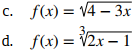
Solución:

1. No puede dividir por cero, por lo que el dominio es el conjunto de valores x tal que x² − 1 ≠ 0. Por lo tanto, el dominio es {x | x ≠ ± 1}.
2. Necesita determinar los valores de x para los cuales el denominador es diferente de cero. Como 3x² + 4 ≥ 4 para todos los números reales x, el denominador nunca es cero. Por lo tanto, el dominio es (−∞, ∞).
3. Como la raíz cuadrada de un número negativo no es un número real, el dominio es el conjunto de valores x para los cuales 4 − 3x ≥ 0. Por lo tanto, el dominio es {x|x ≤ 4/3}.
4. La raíz cúbica se define para todos los números reales, por lo que el dominio es el intervalo (−∞, ∞).

EJERCICIO DE CONTROL 1.2_4 

Encuentre el dominio para cada una de las siguientes funciones: f (x) = (5 − 2x)/(x² + 2) y g(x) = √(5x − 1).

Funciones trascendentes

Hasta ahora, hemos discutido las funciones algebraicas. Sin embargo, algunas funciones no pueden describirse mediante operaciones algebraicas básicas. Estas funciones se conocen como funciones trascendentes porque se dice que “trascienden” o van más allá del álgebra. Las funciones trascendentales más comunes son las funciones trigonométricas, exponenciales y logarítmicas. Una función trigonométrica relaciona las razones de dos lados de un triángulo rectángulo. Son senx, cosx, tanx, cotx, secx y cscx. (Discutiremos las funciones trigonométricas más adelante en el capítulo). Una función exponencial es una función de la forma f (x) = b˟, donde la base b > 0, b ≠ 1. Una función logarítmica es una función de la forma f (x) = log_b (x) para alguna constante b > 0, b ≠ 1, donde log_b (x) = y si y sólo si bʸ = x. (También discutimos funciones exponenciales y logarítmicas más adelante en este capítulo).

EJEMPLO ILUSTRATIVO 1.2_7. Clasificación de funciones algebraicas y trascendentales

Clasifique cada una de las siguientes funciones, como algebraica o trascendente.

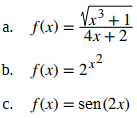
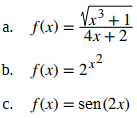
Solución:

1. Dado que esta función involucra solo operaciones algebraicas básicas, es una función algebraica.
2. Esta función no se puede escribir como una fórmula que involucra solo operaciones algebraicas básicas, por lo que es trascendente. (Tenga en cuenta que las funciones algebraicas solo pueden tener potencias que sean números racionales).
3. Como en la parte b., Esta función no puede escribirse usando una fórmula que involucre únicamente operaciones algebraicas básicas; por lo tanto, esta función es trascendental. ◊

EJERCICIO DE CONTROL 1.2_5

¿Es f (x) = x/2 una función algebraica o trascendente?

Funciones definidas por tramos

A veces, una función se define mediante diferentes fórmulas en diferentes partes de su dominio. Una función con esta propiedad se conoce como una función definida por tramos. La función de valor absoluto es un ejemplo de una función definida por tramos porque la fórmula cambia con el signo de x:

Otras funciones definidas por tramos pueden estar representadas por fórmulas completamente diferentes, dependiendo de la parte del dominio en el que cae un punto. Para graficar una función definida por tramos, graficamos cada parte de la función en su dominio respectivo, en el mismo sistema de coordenadas. Si la fórmula para una función es diferente para x < a  y  x > a, debemos prestar especial atención a lo que sucede en x = a cuando graficamos la función. A veces, el gráfico debe incluir un círculo abierto o cerrado para indicar el valor de la función en x = a. Lo examinamos en el siguiente ejemplo.

EJEMPLO ILUSTRATIVO 1.2_8. Graficar una función definida por tramos

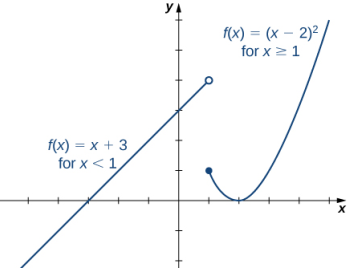
Dibuje la gráfica de la siguiente función definida por tramos:

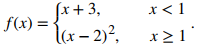
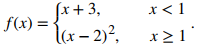
Solución:
Representa gráficamente la función lineal y = x + 3 en el intervalo (−∞, 1) y representa gráficamente la función cuadrática y = (x − 2)² en el intervalo [1, ∞). Dado que el valor de la función en x = 1 viene dado por la fórmula f (x) = (x − 2)², vemos que f (1) = 1. Para indicar esto en la gráfica, dibujamos un círculo cerrado en el punto (1, 1). El valor de la función viene dado por f (x) = x + 2 para todo x < 1, pero no en x = 1. Para indicar esto en la gráfica, dibujamos un círculo abierto en (1, 4).

EJERCICIO DE CONTROL 1.2_6

Dibuja la gráfica de la función

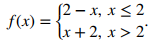
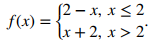
EJEMPLO ILUSTRATIVO 1.2_9. Tarifas de estacionamiento descritas por una función definida por tramos

En una gran ciudad, a los conductores se les cobra una tarifa variable por estacionarse en un estacionamiento. Se les cobra $10 por la primera hora o cualquier parte de la primera hora y $2 adicionales por cada hora o parte de la misma hasta un máximo de $30 por día. El estacionamiento está abierto de 6 a.m. a 12 de la medianoche.

1. Escriba una función definida por tramos que describa el costo C para aparcar en el estacionamiento en función de las horas estacionadas x.
2. Dibuje una gráfica de esta función C(x).

Solución:

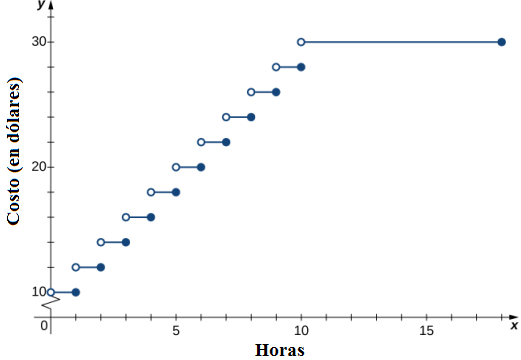
a.  Como el estacionamiento está abierto 18 horas al día, el dominio para esta función es {x| 0 < x ≤ 18}. La función definida por tramos que describe el costo de aparcar un automóvil en este estacionamiento es la siguiente:

b.  La gráfica de la función consta de varios segmentos de línea horizontal:

EJERCICIO DE CONTROL 1.2_7

El costo de enviar una carta es una función del peso de la carta. Suponga que el costo de enviar una carta por correo es de 49 ¢ por la primera onza y 21 ¢ por cada onza adicional. Escriba una función definida por tramos que describa el costo C como una función del peso x para 0 < x ≤ 3, donde C se mide en centavos y x se mide en onzas.

Transformaciones de funciones

Hemos visto varios casos en los que hemos agregado, restado o multiplicado constantes para formar variaciones de funciones simples. Por ejemplo, podemos restar 2 del argumento de la función y = x² para obtener la función f (x) = (x − 2)². Esta resta representa un desplazamiento de la función y = x² dos unidades a la derecha. Un cambio, horizontal o vertical, es un tipo de transformación de una función. Otras transformaciones incluyen escalas horizontales y verticales, y reflexiones sobre los ejes.

Se produce un desplazamiento vertical de una función si sumamos o restamos la misma constante a cada salida y. Para c > 0, la gráfica de f (x) + c es un desplazamiento de la gráfica de f (x) hacia arriba c unidades, mientras que la gráfica de f (x) − c es un desplazamiento de la gráfica de f (x) hacia abajo c unidades. Por ejemplo, la gráfica de la función f (x) = x³ + 4 es la gráfica de y = x³ desplazada hacia arriba 4 unidades; la gráfica de la función f (x) = x³ − 4 es la gráfica de y = x³ desplazada hacia abajo 4 unidades (Figura 1.2_8).

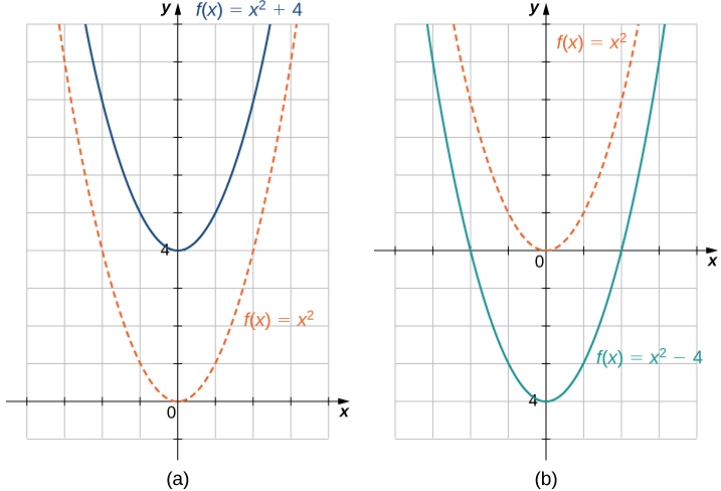
Se produce un desplazamiento horizontal de una función si sumamos o restamos la misma constante a cada entrada x. Para c > 0, la gráfica de f (x + c) es un desplazamiento de la gráfica de f (x) c unidades hacia la izquierda; la gráfica de f (x − c)  es un desplazamiento de la gráfica de f (x) hacia la derecha de c unidades. ¿Por qué la gráfica se desplaza hacia la izquierda al sumar una constante y hacia la derecha al restar una constante? Para responder esta pregunta, veamos un ejemplo.

Considere la función f (x)  = |x + 3| y evalúe esta función en x − 3. Como f (x − 3) = |x|  y  x − 3 < x, la gráfica de f (x) = |x + 3| es la gráfica de y = |x| desplazado a la izquierda 3 unidades. Del mismo modo, la gráfica de f (x) = |x − 3| es la gráfica de y = |x| desplazada a la derecha 3 unidades (Figura 1.2_9).

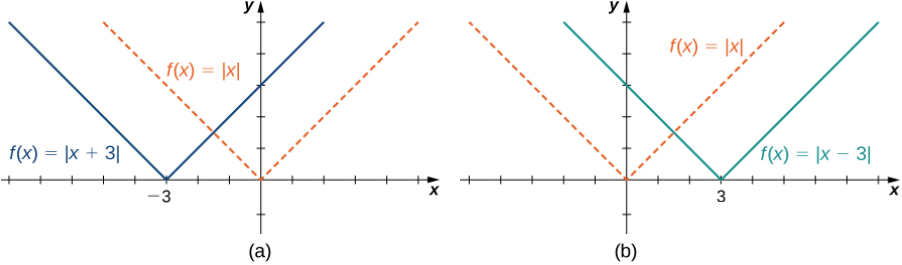
Se produce una escala vertical de una gráfica si multiplicamos todas las salidas y de una función por la misma constante positiva. Para c > 0, la gráfica de la función cf (x) es la gráfica de f (x) escalada verticalmente por un factor c. Si c > 1, los valores de las salidas para la función cf (x) son mayores que los valores de las salidas para la función f (x); por lo tanto, la gráfica se ha estirado verticalmente. Si 0 < c < 1, entonces las salidas de la función cf (x) son más pequeñas, por lo que el gráfico se ha comprimido. Por ejemplo, la gráfica de la función f (x) = 3x² es la gráfica de y = x² estirada verticalmente por un factor de 3, mientras que la gráfica de la función f (x) = x²/3 es la gráfica de y = x² comprimida verticalmente por un factor de 3 (Figura 1.2_10).

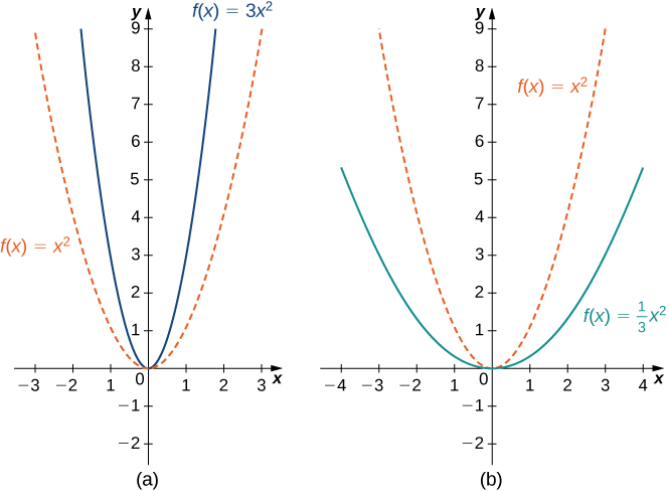
La escala horizontal de una función ocurre si multiplicamos las entradas x por la misma constante positiva. Para c > 0, la gráfica de la función f (cx) es la gráfica de f (x) escalada horizontalmente por un factor de c. Si c > 1, la gráfica de f (cx) es la gráfica de f (x) comprimida horizontalmente. Si 0 < c < 1, la gráfica de f (cx) es la gráfica de f (x) estirada horizontalmente. Por ejemplo, considere la función considere la función f (x) = √2x y evalúe f en x/2. Como f (x/2) = √x, la gráfica de f (x) = √2x  es la gráfica de y = √x  comprimida horizontalmente. La gráfica de y = √(x/2) √ es un tramo horizontal de la gráfica de y = √x (figura 1.2_11)

Hemos explorado lo que le sucede a la gráfica de una función f cuando multiplicamos f por una constante c > 0 para obtener una nueva función cf (x). También hemos discutido lo que le sucede a la gráfica de una función f cuando multiplicamos la variable independiente x por c > 0 para obtener una nueva función f (cx). Sin embargo, no hemos abordado lo que le sucede a la gráfica de la función si la constante c es negativa. Si tenemos una constante c < 0, podemos escribir c como un número positivo multiplicado por −1; pero, ¿qué tipo de transformación obtenemos cuando multiplicamos la función o su argumento por −1? Cuando multiplicamos todas las salidas por −1, obtenemos una reflexión sobre el eje x. Cuando multiplicamos todas las entradas por −1, obtenemos una reflexión sobre el eje y. Por ejemplo, la gráfica de f (x) = – (x³ + 1) es la gráfica de y = (x³ + 1) reflejada sobre el eje x. La gráfica de f (x) = (- x)³ + 1 es la gráfica de y = x³ + 1 reflejada sobre el eje y (Figura 1.2_12).

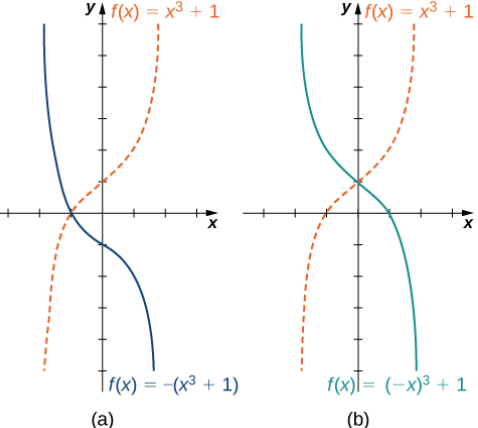
Si la gráfica de una función consiste en más de una transformación de otra gráfica, es importante transformar la gráfica en el orden correcto. Dada una función f (x), la gráfica de la función relacionada y = cf (a (x + b)) + d se puede obtener de la gráfica de y = f (x) realizando las transformaciones en el siguiente orden:

1. Desplazamiento horizontal de la gráfica de y = f (x). Si b > 0, desplaza a la izquierda. Si b < 0, desplaza a la derecha.
2. Escalado horizontal de la gráfica de y = f (x + b) por un factor de | a |. Si a  < 0, refleja la gráfica sobre el eje y.
3. Escalado vertical de la gráfica de y = f (a (x + b)) por un factor de | c |. Si c < 0, refleje la gráfica sobre el eje x.
4. Desplazamiento vertical de la gráfica de y = cf (a (x + b)). Si d > 0, desplazarse hacia arriba. Si d < 0, cambia hacia abajo.

Podemos resumir las diferentes transformaciones y sus efectos relacionados en el gráfico de una función en la siguiente tabla.

Transformación de f , c > 0	Efecto en la gráfica de f
f (x) + c	Desplazamiento vertical hacia arriba c unidades
f (x) − c	Desplazamiento vertical hacia abajo c unidades
f (x + c)	Desplazamiento hacia la izquierda por c unidades
f (x − c)	Desplazar a la derecha por c unidades
cf (x)	Estiramiento vertical si c  > 1; compresión vertical si 0 < c <1
f (cx)	Estiramiento horizontal si 0 < c < 1; compresión horizontal si c > 1
−f (x)	Reflexión sobre el eje x
f (−x)	Reflexión sobre el eje y

EJEMPLO ILUSTRATIVO 1.2_10. Transformando una Función

Para cada una de las siguientes funciones, a. y b., dibuje una gráfica usando una secuencia de transformaciones de una función bien conocida.

Solución:
a.  Comenzando con la gráfica de y = |x|, desplace 2 unidades hacia la izquierda, reflexione sobre el eje x, y luego desplace hacia abajo 3 unidades.

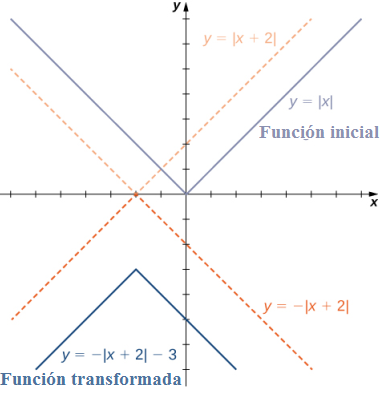
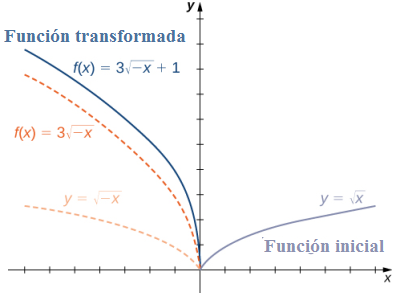
b.  Comenzando con la gráfica de y =√x , reflexione sobre el eje y, estire la gráfica verticalmente por un factor de 3 y suba 1 unidad.