| 1. Funciones y sus gráficas | 1.2. Clases básicas de funciones |
Polinomios
Una función lineal es un tipo especial de una clase de funciones más general: las funciones polinomiales.
Función polinomial
Una función polinomial o polinómica es cualquier función que se puede escribir en la forma
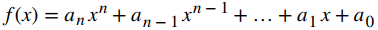
para algunos enteros n ≥ 0 y constantes an, an − 1, …, a0, donde an ≠ 0.
En el caso de n = 0 y a0 = 0, se tiene la función f (x) = 0 que se llama función cero.
El valor de n da el grado del polinomio; la constante an se denomina coeficiente principal.
Una función lineal de la forma f (x) = mx + b es un polinomio de grado 1 si m ≠ 0 y grado 0 si m = 0. Un polinomio de grado 0 también se llama función constante.
Una función polinomial de grado 2 se denomina función cuadrática. En particular, una función cuadrática tiene la forma
f (x) = ax² + bx + c, donde a ≠ 0.
Una función polinómica de grado 3 se llama función cúbica.
Función potencia
Algunas funciones polinomiales son funciones de potencia. Una función potencia es una función de la forma
f (x) = axᵇ, donde a y b son cualquier número real.
El exponente en una función de potencia puede ser cualquier número real, pero aquí consideramos el caso cuando el exponente es un número entero positivo. (Consideramos otros casos más adelante).
Si el exponente es un entero positivo, entonces
f (x) = axⁿ es un polinomio.
Si n es par, entonces f (x) = axⁿ es una función par porque f (−x) = a(−x)ⁿ = axⁿ si n es par.
Si n es impar, entonces f (x) = axⁿ es una función impar porque f (−x) = a(−x)ⁿ = −axⁿ si n es impar (Figura 1.2_4
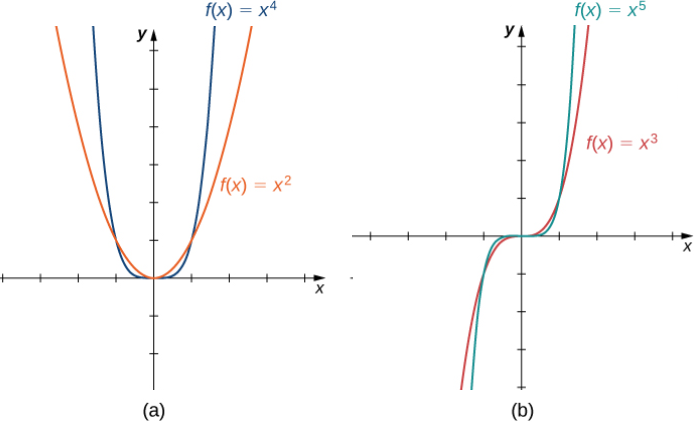
(Figura 1.2_4(a) Para cualquier número entero par n, f (x) = axⁿ es una función par.
(b) Para cualquier número entero impar n, f (x) = aⁿ es una función impar.)
Comportamiento en el infinito
Para determinar el comportamiento de una función f cuando las entradas tienden al infinito observamos los valores de f (x) a medida que las entradas, x, se hacen más grandes. Para algunas funciones, conforme x toma valores cada vez más grandes, los valores de f (x) se acercan a un número finito. Por ejemplo, para la función f (x) = 2 + 1/x, los valores 1 / x se aproximan cada vez más a cero a medida que los valores de x se hacen más y más grandes. Para esta función, decimos que “f (x) se aproxima a dos cuando x va al infinito”, y escribimos f (x) → 2 cuando x → ∞. La recta y = 2 es una asíntota horizontal para la función f (x) = 2 + 1/x porque la gráfica de la función se acerca a esta recta a medida que x se hace más grande.
Para otras funciones, los valores f (x) pueden no aproximarse a un número finito, sino que pueden aumentar también a medida que los valores de x aumentan. En ese caso, decimos que “f (x) tiende al infinito conforme x tiende al infinito”, y escribimos f (x) → ∞ cuando x → ∞. Por ejemplo, para la función f (x) = 3x², las salidas f (x) se hacen más grandes a medida que las entradas x se hacen más grandes. Podemos concluir que la función f (x) = 3x² tiende al infinito cuando x tiende al infinito, y escribimos 3x² → ∞ cuando x → ∞.
El comportamiento cuando x → −∞ y el significado de f (x) → −∞ cuando x → ∞ o x → −∞ se pueden definir de manera similar. Podemos describir lo que sucede con los valores de f (x) cuando x → ∞ y cuando x → −∞ como el comportamiento final de la función.
Comportamiento de las funciones polinomiales
Para comprender el comportamiento final de las funciones polinomiales, podemos centrarnos en las funciones cuadráticas y cúbicas. El comportamiento de los polinomios de mayor grado se puede analizar de manera similar.
Considere la función cuadrática f (x) = ax² + bx + c. Si a > 0, los valores f (x) → ∞ cuando x → ± ∞. Si a < 0, los valores f (x) → −∞ cuando x → ± ∞. Como la gráfica de una función cuadrática es una parábola, la parábola abre hacia arriba si a > 0 y la parábola abre hacia abajo si a < 0. (Ver Figura 1.2_5 (a).)
Ahora considere una función cúbica f (x) = ax³ + bx² + cx + d. Si a > 0, entonces f (x) → ∞ cuando x → ∞ y f (x) → −∞ cuando x → −∞. Si a < 0, entonces f (x) → −∞ cuando x → ∞ y f (x) → ∞ cuando x → −∞. Como podemos ver en estas dos gráficas, el término principal del polinomio determina el comportamiento final. (Ver Figura 1.2_5 (b)).
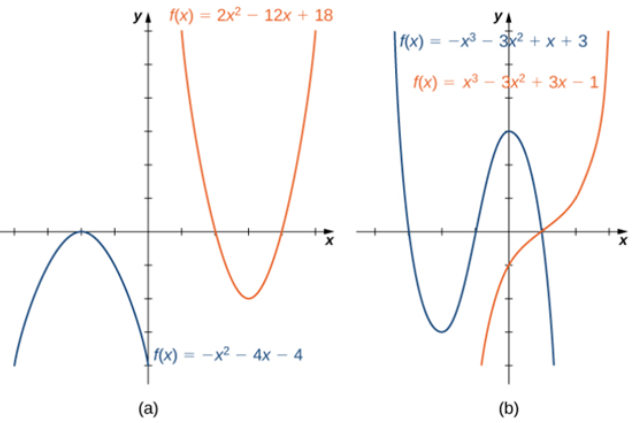
Ceros de funciones polinomiales
Otra característica de la gráfica de una función polinomial es donde intersecta el eje x. Para determinar dónde una función f se cruza con el eje x, necesitamos resolver la ecuación f (x) = 0; por ejemplo, en el caso de la función lineal f (x) = mx + b, la intersección x se obtiene resolviendo la ecuación mx + b = 0. En este caso, vemos que la intersección x está dada por (−b/m, 0). En el caso de una función cuadrática, encontrar la(s) intersección(es) x requiere calcular los ceros de una ecuación cuadrática: ax² + bx + c = 0. En algunos casos, es fácil factorizar el polinomio ax² + bx + c para encontrar los ceros. Si no, hacemos uso de la fórmula cuadrática.
REGLA: LA FÓRMULA CUADRÁTICA
Considere la ecuación cuadrática
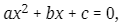
donde a ≠ 0. Las soluciones de esta ecuación están dadas por la fórmula cuadrática

Si el discriminante b² − 4ac > 0, esta fórmula nos dice que hay dos números reales que satisfacen la ecuación cuadrática. Si b^2 − 4ac = 0, esta fórmula nos dice que solo hay una solución, y es un número real. Si b² − 4ac < 0, ningún número real satisface la ecuación cuadrática.
En el caso de los polinomios de mayor grado, puede ser más complicado determinar dónde corta la gráfica el eje x. En algunos casos, es posible encontrar las intersecciones x factorizando el polinomio para encontrar sus ceros. En otros casos, es imposible calcular los valores exactos de las intersecciones x. Sin embargo, como veremos más adelante en estas lecciones, en casos como este, podemos usar herramientas analíticas para aproximar (en un grado muy alto) dónde se encuentran los interceptos x. Aquí nos centramos en los gráficos de polinomios para los cuales podemos calcular sus ceros explícitamente.
EJEMPLO ILUSTRATIVO 1.2_3. Graficando funciones polinomiales
Para las siguientes funciones a. y b., i. describa el comportamiento de f (x) cuando x → ± ∞, ii. encontrar todos los ceros de f, y iii. bosqueja una gráfica de f.
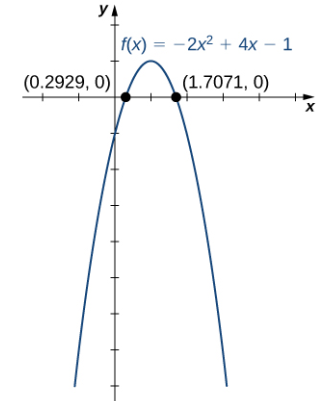
a. f (x) = – 2x² + 4x − 1
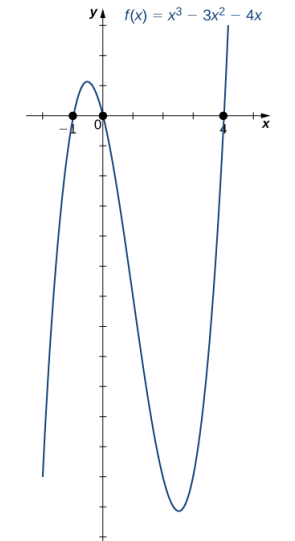
b. f (x) = x³ − 3x² − 4x
Solución:
a. La función f (x) = – 2x² + 4x − 1 es una función cuadrática.
i. Como a = −2 < 0, cuando x → ± ∞, f (x) → −∞.
ii. Para encontrar los ceros de f, usa la fórmula cuadrática. Los ceros son

iii. Para dibujar la gráfica de f, use la información de sus respuestas anteriores y combínalo con el hecho de que la gráfica es una parábola que se abre hacia abajo.
b. La función f (x) = x³ − 3x² − 4x es una función cúbica.
i. Como a = 1 > 0, cuando x → ∞, f (x) → ∞. Cuando x → −∞, f (x) → −∞.
ii. Para encontrar los ceros de f, necesitamos factorizar el polinomio. Primero, sacamos factor común x,
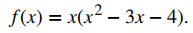
Entonces, cuando factorizamos la función cuadrática x² − 3x − 4, encontramos
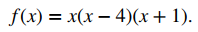
Por lo tanto, los ceros de f son x = 0, 4, −1.
iii. Combinando los resultados de las partes i. y ii., dibuje un bosquejo aproximado de f.
EJERCICIO DE CONTROL 1.2_2
Considere la función cuadrática f (x) = 3x² − 6x + 2. Encuentra los ceros de f. ¿La parábola abre hacia arriba o abre hacia abajo?

Cómo determinar la paridad de la función y=2x-6
Hola. La función y = f(x) = 2x – 6 no es par ni impar.
• Una función es par si f(–x) = f(x).
• Una función es impar si f(–x) = –f(x)