Miscelánea de ejercicios y problemas referentes a la sección 9.1

Zill 1.1_1 a 8 En los problemas 1 a 8 establezca el orden de la ecuación diferencial ordinaria dada. Determine si la ecuación es lineal o no lineal, comparando con la ecuación


Zill 1.1_9 y 10 En los problemas 9 y 10 establezca si la ecuación diferencial de primer orden dada es lineal en la variable dependiente comparándola con la ecuación


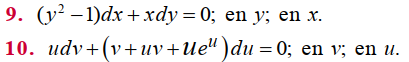
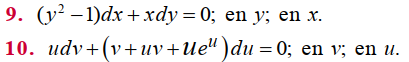
Zill 1.1_11 a 14 En los problemas ll a 14, compruebe que la función indicada es una solución de la ecuación diferencial dada. Suponga un intervalo I de definición adecuado para cada solución.
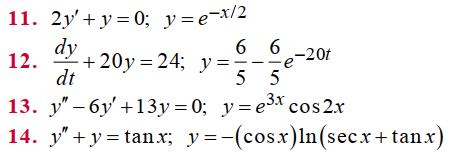
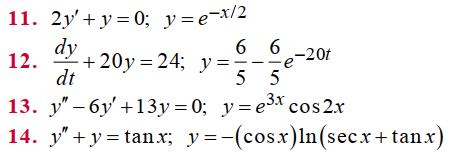
Zill 1.1_15 a 18 En los problemas 15 a 18 compruebe que la función indicada y = f (φ) es una solución explícita de la ecuación diferencial de primer orden dada. Proceda como en el ejemplo 2, considerando a φ simplemente como una función, dando su dominio.
Después considere a φ como una solución de la ecuación diferencial, dando al menos un intervalo I de definición.


Zill 1.1_19 a 20 En los problemas 19 y 20 compruebe que la expresión indicada es una solución implícita de la ecuación diferencial dada. Encuentre al menos una solución explícita
y = θ (x) en cada caso. Use alguna aplicación para trazar gráficas para obtener la gráfica de una solución explícita. Dé un intervalo I de definición de cada solución θ.


Zill 1.1_21 Compruebe que la familia de funciones indicada es una solución de la ecuación diferencial dada. Suponga un intervalo I de definición adecuado para cada solución.


Zill 1.1_22 Compruebe que la familia de funciones indicada es una solución de la ecuación diferencial dada. Suponga un intervalo I de definición adecuado para cada solución.


Zill 1.1_23 Compruebe que la familia de funciones indicada es una solución de la ecuación diferencial dada. Suponga un intervalo I de definición adecuado para cada solución.


Zill 1.1_24 Compruebe que la familia de funciones indicada es una solución de la ecuación diferencial dada. Suponga un intervalo I de definición adecuado para cada solución.


Zill 1.1_25 Compruebe que la función definida por tramos


Zill 1.1_27 Determine los valores de m tales que la función
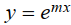
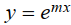
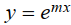
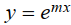
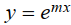
sea una solución de la ecuación diferencial


Zill 1.1_28 Determine los valores de m tales que la función
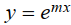
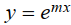
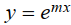
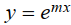
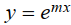
sea una solución de la ecuación diferencial


Zill 1.1_29 Determine los valores de m tales que la función
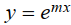
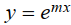
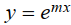
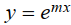
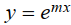
sea una solución de la ecuación diferencial


Zill 1.1_30 Determine los valores de m tales que la función
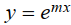
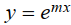
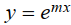
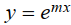
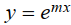
sea una solución de la ecuación diferencial


Zill 1.1_31 Determine los valores de m tales que la función



sea una solución de la ecuación diferencial


Zill 1.1_32 Determine los valores de m tales que la función



sea una solución de la ecuación diferencial


Zill 1.1_ 33 a 36 Use el concepto de que
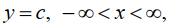
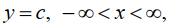
es una función constante si y sólo si y ′= 0 para determinar si la ecuación diferencial tiene soluciones constantes:








Zill 1.1_37 y 38 Compruebe que el par de funciones indicado es una solución del sistema dado de ecuaciones diferenciales en el intervalo (-∞, ∞ ):






MAI. Zill 1.1_39 Dado que y = sen x es una solución explícita de la ecuación diferencial de primer orden


Encuentre un intervalo de definición I.
MAI. Zill 1.1_40 Analice por qué tiene sentido suponer que la ecuación diferencial lineal y ” + 2y ‘ + 4y = 5sent cuenta con una solución del tipo y = A sen t + B cos t, donde A y B son constantes. Luego encuentre las constantes A y B específicas de modo que y = A sen t + B cos t sea una solución particular de la ecuación diferencial.
MAI. Zill 1.1_43 Las gráficas de los miembros de la familia de un parámetro x³ + y³ = 3cxy se denomina folia de Descartes. Verifique si esta familia es una solución implícita de la ecuación diferencial de primer orden:


Zill 1.2_1 La siguiente función



es una familia uniparamétrica de soluciones de la ED de primer orden y ‘ = y – y². Encuentre una solución del PVI de primer orden que consiste en esta ecuación diferencial y la condición inicial
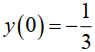
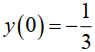
Zill 1.2_2 La siguiente función



es una familia uniparamétrica de soluciones de la ED de primer orden y ‘ = y – y². Encuentre una solución del PVI de primer orden que consiste en esta ecuación diferencial y la condición inicial


Zill 1.2_3 La función y = 1/(x² + c) es una familia uniparamétrica de soluciones de la ED de primer orden y ‘ + 2xy² = 0. Determine una solución de PVI de primer orden que consiste en esta ecuación diferencial y la condición inicial y(2) = 1/3. Dé el intervalo I más largo en el que está definida la solución.



Excelente explicación