Introducción a las ecuaciones diferenciales

Ejercicios propuestos para la sección 9.1

Determine el orden de las siguientes ecuaciones diferenciales:

Verifique que las siguientes funciones son soluciones a la ecuación diferencial dada:

Verifique las siguientes soluciones generales y encuentre la solución particular pedida:

18. Encuentre la solución particular a la ecuación diferencial y′ = 4x² que pasa por el punto (−3, −30), dado que y = C + 4x³/3 es la solución general.

19. Encuentre la solución particular a la ecuación diferencial y′ = 3x³ que pasa por el punto (1, 4.75), dado que y = C + 3x⁴/4 es la solución general.

20. Encuentre la solución particular a la ecuación diferencial y′ = 3x²y que pasa por el punto (0, 12), dado quees la solución general.

21. Encuentre la solución particular a la ecuación diferencial y′ = 2xy que pasa por (0, 1/2), dado quees la solución general. (Ver la solución en video)

22. Encuentre la solución particular a la ecuación diferencial y′ = (2xy)² que pasa por el punto (1, −1/2), dado que y = −3/(C + 4x³) es la solución general.

23. Encuentre la solución particular a la ecuación diferencial y′x² = y que pasa por (1, 2/e), dado quees la solución general.

24. Encuentre la solución particular a la ecuación diferencial 8dx/dt = −2cos(2t) − cos(4t) que pasa por el punto (π, π), dado que x = C − sen(2t)/8 − sen(4t)/32 es la solución general.

25. Encuentre la solución particular a la ecuación diferencial du/dt = tanu que pasa por el punto (1, π/2), dado quees la solución general.

26. Encuentre la solución particular a la ecuación diferencialque pasa por el punto (1, 0), dado que y = −ln(C − eᵗ) es la solución general.

27. Encuentre la solución particular a la ecuación diferencial y′(1 − x²) = 1 + y que pasa por el punto (0, −2), dado que es la solución general. (Ver la solución en video)

Para los siguientes problemas, encuentre la solución general a la ecuación diferencial dada.

Resuelva los siguientes problemas de valor inicial a partir de y(t = 0) = 1 e y(t = 0) = – 1. Dibuja ambas soluciones en el mismo gráfico.

Resuelva los siguientes problemas de valor inicial a partir de yo = 10. ¿A qué hora aumenta y a 100 o cae a 1?

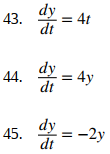
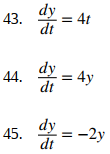
Recuerde que una familia de soluciones incluye soluciones a una ecuación diferencial que difieren en una constante. Para los siguientes problemas, use su calculadora para graficar una familia de soluciones a la ecuación diferencial dada. Use condiciones iniciales de y(t = 0) = – 10 a y(t = 0) = 10 aumentando en 2. ¿Hay algún punto crítico en el que el comportamiento de la solución comienza a cambiar?

53. Encuentre la solución general para describir la velocidad de una bola de masa de 1 lb que se lanza hacia arriba a una velocidad por pie/segundo.

54. En el problema anterior, si la velocidad inicial de la pelota lanzada al aire es a = 25 pies/s, escriba la solución particular a la velocidad de la pelota. Resuelve para encontrar el momento en que la pelota toca el suelo.

55. Se lanzan dos objetos con diferentes masas m₁ y m₂ hacia arriba en el aire con la misma velocidad inicial en pies/s. ¿Cuál es la diferencia en su velocidad después de 1 segundo?

56. [T] Si lanzas una bola de masa 1 kilogramo hacia arriba con una velocidad de a = 25 m/s en Marte, donde la fuerza de gravedad es g = −3.711 m/s². Usa tu calculadora para aproximar cuánto tiempo más está la pelota en el aire en Marte.

57. [T] Para el problema anterior, usa tu calculadora para aproximar cuánto más alto fue la bola en Marte.

58. [T] Un automóvil en la autopista acelera según a = 15cos(πt), donde t se mide en horas. Configure y resuelva la ecuación diferencial para determinar la velocidad del automóvil si tiene una velocidad inicial de 51 mph. Después de 40 minutos de conducción, ¿cuál es la velocidad del conductor?

59. [T] Para el automóvil en el problema anterior, encuentre la expresión de la distancia que ha recorrido el automóvil en el tiempo t, suponiendo una distancia inicial de 0. ¿Cuánto tiempo le toma al automóvil recorrer 100 millas? Redondea tu respuesta a horas y minutos.

60. [T] Para el problema anterior, encuentre la distancia total recorrida en la primera hora.

61. Sustituya y = Be³ᵗ en y′ − y = 8e³ᵗ para encontrar una solución particular.

62. Sustituya y = acos(2t) + bsen (2t) en y′ + y = 4sen(2t) para encontrar una solución particular.

63. Sustituya y = a + bt + ct² en y′ + y = 1 + t^² para encontrar una solución particular.

64. Sustituya y = aeᵗcost + beᵗsent en y′ = 2eᵗcost para encontrar una solución particular.

65. Resuelva y′ = eᵏᵗ con la condición inicial y(0) = 0 y resuelva y′ = 1 con la misma condición inicial. Cuando k se acerca a 0, ¿qué notas?